Задача 21. Проверка простого числа

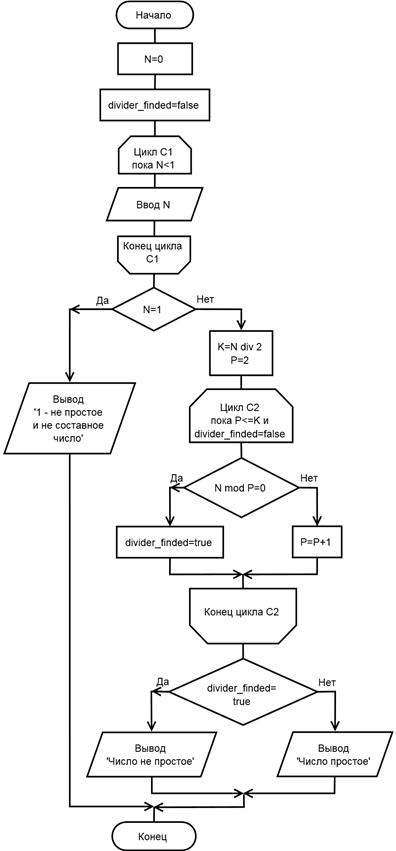
Условие задачи. Дано натуральное число N. Проверить, является ли оно простым.

Простым называется натуральное число, имеющее ровно два различных делителя: единицу и самого себя. Следовательно, для проверки натурального числа N на простоту необходимо убедится, что оно больше 1 и делится без остатка только на 1 и самого себя. Можно заметить, что числа, большие, чем N div 2 (где операция a div b – целочисленное деление) делителями числа N быть не могут - это следует из теории чисел. Следовательно, так как любое натуральное число N > 1 однозначно делится на 1 и самого себя, то для утверждения об отсутствии других делителей необходимо убедиться, что оно не делится без остатка на какие-либо другие натуральные числа из диапазона от 2 до N div 2 включительно. При этом достаточно найти в нем хотя бы одно число P такое что N mod P = 0, чтобы утверждать, что число N не является простым, и в этом случае нет необходимости проверять весь диапазон.

Для реализации проверки наличия у числа N хотя бы одного делителя из диапазона от 2 до N div 2 включительно воспользуемся алгоритмической конструкцией «цикл с предусловием» и логической переменной divider _ finded (изначально имеющей значение «ложь», обозначенное как False), обеспечивающей завершение цикла по нахождению делителя до исчерпания диапазона и сохранению результата – был ли пройден весь диапазон без нахождения или был найден делитель. Тогда, если считать, что логическая переменная может принимать два значения «Истина» и «Ложь», обозначаемые как True и False (в конкретных языках программирования могут использоваться другие обозначения или в качестве логических могут рассматриваться выражения других типов), можно записать алгоритм следующим образом:

Структурированная запись алгоритма 21

1. N = 0

2. divider_finded = False

3. Пока N меньше 1, повторять:

Ввести значение переменной N.

4. Если N равно 1, то:

4.1. Вывести сообщение «Введена единица (не простое и не составное число)»

   Иначе:

4.2. K = N div 2

4.3. P = 2

4.4. Пока P £ K и divider _ finded равно False, повторять:

4.4.1. Если N mod P равно 0, то:

4.4.1.1. divider_finder = True

Иначе:

4.4.1.2. P = P + 1

4.5. Если divider_finder равно True, то:

4.5.1. Вывести сообщение «Введенное число не является простым»

Иначе:

4.5.1. Вывести сообщение «Введенное число является простым».

Схема алгоритма

Программа на языке Си

#include <stdio.h>

#include <stdlib.h>

/* Программа подготовлена с помощью Dev-C++ 5.11

*/

int main(int argc, char *argv[]) {

int N, K, P;

int divider_finded = 0;

/* Целое, равное 0 -- "ложь" */

while(N < 1){

printf("Введите натуральное число N: ");

scanf("%d", &N);

}

if(N == 1)

{

printf("Введена единица (не простое");

  printf(" и не составное число)\n");

}

else

{

   K = N / 2;

   P = 2;

while(P<=K &&!divider_finded) 

    if(N % P == 0)

       divider_finded = -128;

    /* Все, что не равно 0 -- "истина" */

    else

       P++;

if(divider_finded)

/* Аналогично if(divider_finded!= 0) */

    printf("Число не является простым");

else

    printf("Число является простым");

}

system("pause");

return 0;

}

Программа на языке Паскаль

Program Pr_21;

Var

K, N, P: integer;

divider_finded: boolean;

begin

N:=0;

divider_finded:=false;

while N<1 do

begin

writeln(' Введите натуральное число N: ');

readln(N);

end;

if N=1 then

begin

writeln(' Введена единица (не простое ',

        ' и не составное число)');

end

else

begin

K:=N div 2;

P:=2;

while (P<=K) and not divider_finded do

       if N mod P = 0 then

       divider_finded:= true

    else

       P:=P+1;

if divider_finded then

{ Аналогично if divider_finded = true }

    writeln(' Число не является простым ')

else

    writeln(' Число является простым ');

end;

end.

Программа на языке Фортран

Program Pr_21

Implicit none

integer K, N/0/, P

logical divider_finded

divider_finded=.false.

do while (N<1)

print *, ' Введите натуральное число N: '

read *, N

enddo

if (N==1) then

print *,' Введена единица (не простое ', &

        ' и не составное число)'

else

K = N/2

P = 2

do while (P<=K.and..not.divider_finded)

       if (mod(N,P) == 0) then

       divider_finded=.true.

    else

       P = P+1

    endif

enddo

if (divider_finded) then

{ Аналогично if (divider_finded ==.true.) }

    print *,' Число не является простым '

else

    print *,' Число является простым '

endif

endif

end

Программа на языке Python

N = 0

divider_finded = False

while N < 1:

print("Введите натуральное число N: ")

N=int(input())

if N == 1:

print("Введена единица ")

print("(не простое и не составное число)")

else:

K = N // 2

P = 2

while P <= K and not divider_finded:

if N % P == 0:

  divider_finded = True

else:

P = P + 1

if divider_finded:

print("Введенное число не является простым")

else:

print("Введенное число является простым")

Программа в системе Матлаб

N=0;

divider_finded=false;

while N<1

N=input('Введите натуральное число N');

end

if N == 1

disp('Введена единица ')

disp('(не простое и не составное число)')

else

K=N/2;

P=2;

while P<=K && ~ divider_finded

if rem(N,P)==0

    divider_finded=true;

else

    P=P+1;

end

end

if divider_finded

disp('Число не является простым')

else

disp('Число является простым')

end

end