Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 6. Использование вложенных условных конструкций для решения уравненияСодержание книги
Поиск на нашем сайте
Условие задачи. Даны целые a и b. Найти решение уравнения Чтобы составить алгоритм и написать программу решения данной задачи, надо знать, как математически найти корни уравнения вида - при а =0 и b =0 корнем уравнения х может быть любое число; - при а =0, а b ≠0 решений нет; - при а ≠0, а b =0 корень х =0; - при а ≠0 и b ≠0 если а и b имеют разный знак, то решений нет, а если а и b имеют одинаковый знак, то уравнение имеет два корня х =± b / a. Поэтому при составлении алгоритма нужно предусмотреть проверку различных условий, что на структурной схеме изображается блоками «ветвление», а в программной реализации - вложенными условными операторами. Заметим, что для проверки знаков коэффициентов a и b можно использовать условие «b > 0 и a >0 или b <0 и a <0», а можно проверить знак произведения a и b «a * b >0» (второй вариант короче). Заметим также, что исходными данными в данной задаче являются два целых числа a и b, а результаты могут быть различными: либо один корень, либо их два, либо корнем может быть любое число, либо корней нет. Поэтому выводиться в зависимости от выполнения условий должны либо вычисленные значения корней, либо соответствующее сообщение. Структурированная запись алгоритма 6 1. Ввести a и b 2. Сравнить а и b с нулем: 2.1. если а =0 и b =0, то вывести «х – любое число» 2.2. если а =0, а b ≠0, то вывести «решения нет» 2.3. если а ≠0, а b =0, то вывести «х =0» 2.4. если а ≠0 и b ≠0,то 2.4.1. если а и b имеют разный знак, то вывести «решения нет» 2.4.2. если а и b одного знака, то вывести + b / a и - b / a Структурная схема алгоритма
Программа на языке Си #include <stdio.h> int main (void) { int a, b; printf (״Введите a и b\n”); scanf (״%lf%lf”, &a, &b); if (a==0) if (b==0) printf (″x - любое число″); else printf (″Решения нет″); else if (b==0) printf (″x = 0″); else if (a*b<0) printf ("Решения нет"); else printf (″x1=%lf x2=%lf”, b/a, -b/a); return 0: } Программа на языке Паскаль Program Pr_6; var a, b: integer; begin writeln ('Введите а и b'); read (a, b); if a=0 then if b=0 then writeln ('х – любое число') else writeln ('Нет решения') else if b=0 then writeln ('x = 0') else if a*b<0 then writeln ('Нет решения') else writeln ('x1=', b/a:8:5, end. Программа на языке Фортран Program Pr_6 Implicit none integer a, b print *, 'Введите а и b' read *, a, b if (a==0) then if (b==0) then print *, 'х – любое число' else print *, 'Нет решения' endif else if (b==0) then print *, 'x = 0' elseif (a*b<0) then print *, 'Нет решения' else print *, 'x1=', b/a, ' x2=', -b/a endif endif end Программа на языке Python print("Введите два целых числа a и b)") print("(по одному в строке)") a = int(input()) b = int(input()) if a == 0: if b == 0: print("x - любое число") else: print("Решения нет") else: if b == 0: print("x = 0") elif a*b < 0: print("Решения нет") else: print("x = ", b/a," или x = ", -b/a)
Программа в системе Матлаб a = input('a='); b = input('b='); if (a==0) if (b==0) disp('х – любое число') else disp('Нет решения') end else if (b==0) disp('x = 0') elseif (a*b<0) disp('Нет решения') else disp(strcat('x1=', num2str (b/a))) disp(strcat('x2=', num2str (-b/a))) end end Циклические алгоритмы Многие процессы в окружающем мире основаны на многократном повторении одной и той же последовательности действий. Каждый год наступают весна, лето, осень и зима. Жизнь растений в течение года проходит одни и те же циклы. Подсчитывая число полных поворотов минутной или часовой стрелки, человек измеряет время. При решении научно-технических, экономических, инженерных задач, как правило, требуется многократное выполнение некоторой совокупности действий с различными значениями, например, для построения таблицы значений какой-либо функции или для обработки результатов многократных замеров некоторых характеристик в процессе эксперимента. Повторяющиеся процессы называются циклическими, соответственно, для их программирования используются циклические алгоритмы, или просто циклы. Циклический алгоритм предусматривает многократное повторение одного и того же действия над одними и теми же данными, значения которых могут изменяться в цикле или оставаться неизменными. К циклическим алгоритмам сводится большинство методов вычислений, требующих перебора вариантов. Однократное выполнение совокупности действий в цикле называется итерацией цикла; описание действий, которые выполняются многократно, составляет тело цикла. Различают 2 вида циклов: арифметические и итерационные. Цикл называют арифметическим, если количество повторений заранее известно или может быть вычислено. Если количество повторений заранее неизвестно, а определяется некоторым условием, то такой цикл называют итерационным. Существуют 3 циклические структуры: цикл с предопределенным количеством повторений, цикл с предусловием, цикл с постусловием. Обычно, когда необходимо выполнять тело цикла для различных значений некоторой переменной в заданном диапазоне, для реализации арифметического цикла удобно использовать конструкцию «цикл с предопределенным количеством повторений». В остальных случаях, когда количество повторений одинаковых действий заранее неизвестно, в зависимости от предполагаемой реализации, можно использовать по своему выбору либо конструкцию «цикл с предусловием», либо конструкцию «цикл с постусловием». Цикл с постусловием применяется при необходимости выполнить какие-либо действия несколько раз, а условие продолжения или окончания цикла проверяется после выполнения каждой итерации. Такой цикл будет выполняться хотя бы один раз. В цикле с предусловием каждый раз до выполнения тела цикла проверяется условие его выполнения, поэтому этот цикл может не выполниться ни одного раза. С помощью конструкции «цикл с предусловием» можно реализовать цикл любого вида. Любой цикл содержит тело цикла, то есть описание действий, которые должны многократно выполняться. Кроме того, циклу обычно предшествует подготовительная часть, в ней присваиваются значения переменным, которые будут использоваться в цикле без изменения, а также задаются начальные значения всех переменных, которые будут в цикле изменяться. Количество повторений тела циклалибо задается (или вычисляется) перед выполнением первой итерации, либо определяется некоторым условием, которое может проверяться либо перед началом выполнения очередной итерации, либо после её окончания. Кроме того, для цикла любого вида можно предусмотреть выход из тела цикла, в результате которого цикл преждевременно завершается; для этого внутри тела цикла должно находиться дополнительное условие завершения цикла. Тело цикла может содержать любые операторы. В том числе возможны ситуации, когда один цикл размещается внутри другого. Такая конструкция называется вложенными циклами или циклом в цикле, или еще их называют кратными или составными. Наружный цикл называют внешним, а вложенные в него - внутренними. Каждый из циклов строится по одинаковым правилам (у них есть подготовительная часть, проверка условия окончания или продолжения и тело цикла). И если один цикл включает в себя другой вложенный цикл, то при каждом выполнении тела наружного цикла внутренний цикл выполняется полностью, то есть на каждой итерации наружного цикла заново многократно выполняются операторы тела внутреннего цикла. Задача 7. Простейший цикл Условие задачи. Получить значения квадратов всех натуральных чисел от 1 до 10. В данной задаче требуется возвести в квадрат и вывести на экран каждое из 10 значений от 1 до 10, то есть 10 раз требуется выполнить одно и то же действие с разными данными, следовательно, нужно использовать цикл. При первом выполнении тела цикла будем возводить в квадрат 1, при втором – 2, при третьем – 3 и так далее до 10, таким образом требуется каждый раз увеличивать возводимое в квадрат число на 1. Предыдущее значение при этом сохранять не требуется, поэтому для получения нового значения на каждом шаге цикла понадобится всего одна целочисленная переменная k. Увеличение значения переменной в цикле на 1 называется изменением с шагом, равным 1. Входных данных у задачи нет, так как интервал задан константами. Выходными данными будут квадраты натуральных чисел из заданного интервала.
|
||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 164; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.18.192 (0.007 с.) |

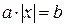 .
.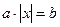 . В зависимости от значений a и b должны быть рассмотрены следующие случаи:
. В зависимости от значений a и b должны быть рассмотрены следующие случаи: