Задача 51. Вспомогательные алгоритмы. Работа с диагоналями двух квадратных матриц

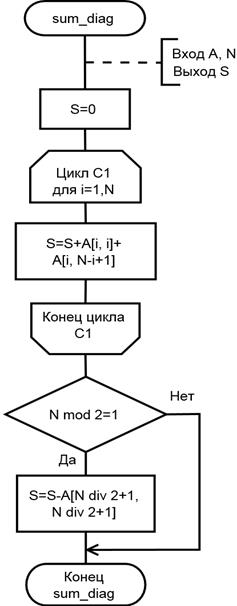
Условие задачи. Даны две квадратные матрицы. Выяснить, в какой из них сумма элементов главной и побочной диагоналей больше.

Поскольку по условию задачи вычисление суммы элементов главной и побочной диагоналей необходимо произвести для двух различных квадратных матриц (возможно разной размерности) для последующего сравнения, то вычисление такой суммы для произвольной квадратной матрицы имеет смысл выделить в самостоятельный алгоритм и воспользоваться им для получения конкретных значений. Для квадратной матрицы A размерностью N x N элементы главной диагонали будут иметь вид A [1,1], A [2,2], …, A [ i, i ], … A [ N, N ] – совпадают номера строки и столбца. Аналогично для побочной диагонали, элементы будут иметь вид A [1, N ], A [2, N–1 ], …, A [ i, N – i +1], … A [ N, 1 ] – номера строк возрастают от 1 к N, а номера столбцов убывают от N до 1. Поскольку количество элементов на главной и побочной диагоналях квадратной матрицы одинаково и равно N, то для вычисления сумм этих элементов можно воспользоваться алгоритмической конструкцией «цикл с предопределенным числом повторений», где в теле цикла на i -й итерации вычисляется сумма элементов A [ i, i ]+ A [ i, N – i +1] главной и побочной диагоналей, принадлежащих к одной строке, и уже она используется для вычисления общей суммы. Обозначив интересующую сумму как S, получим: S = (A [1,1]+ A [1, N ])+(A [2,2]+ A [2, N–1 ])+…+(A [ i, i ]+ A [ i, N – i +1])+… +(A [ N, N ]+ A [ N, 1 ]).

Следует отметить, что при нечетном N элемент, расположенный на пересечении главной и побочной диагонали, будет учтен дважды, что не соответствует условию «сумма элементов главной и побочной диагонали» (и соответствовало бы условию «сумма суммы элементов главной диагонали и суммы элементов побочной диагонали»). Поэтому, если N нечетное (N mod 2 = 1), то после окончания подсчета суммы необходимо вычесть из неё значение центрального элемента A [ N div 2 + 1, N div 2 + 1], где с помощью записи «a div b» показана операция «результат целочисленного деления a на b».

Тогда алгоритм вычисления суммы элементов главной и побочной диагоналей квадратной матрицы A размерностью N x N можно будет записать так:

Структурированная запись алгоритма 51.1

1. Получить от вызывающего алгоритма матрицу A и число строк и столбцов в ней N.

2. S = 0.

3. Повторить для i от 1 до N:

              3.1. S = S + A[i,i]+A[i,N – i+1].

4.1.1. Если N mod 2 = 1, то S = S – A[N div 2 + 1,N div 2 + 1].

4.1.2. Передать вызывающему алгоритму значение переменной S.

Схем а алгоритма 51.1

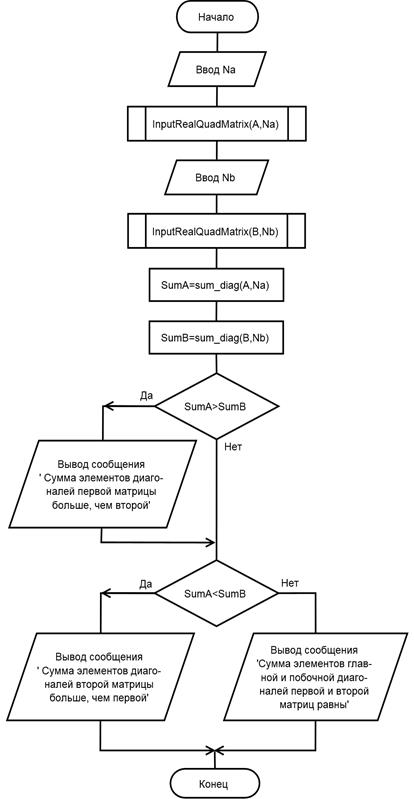
Дадим алгоритму 51.1 собственное имя sum_diag, и обращаясь к нему как функции с двумя аргументами, первый из которых является квадратной матрицей, а второй является числом строк (столбцов) в ней, запишем алгоритм определения матрицы, в которой сумма элементов диагоналей больше:

Структурированная запись алгоритма 51.2

1. Ввеcти Na - число строк матрицы A.

2. Ввести значение переменной A, используя вспомогательный алгоритм InputRealQuadMatrix.

3. Ввести Nb - число строк матрицы B.

4. Ввести значение переменной B, используя вспомогательный алгоритм InputRealQuadMatrix.

5. SumA:= sum_diag(A, Na).

6. SumB:= sum_diag(B, Nb).

7. Если SumA > SumB, то вывести сообщение «сумма элементов главной и побочной диагоналей первой матрицы больше, чем второй», иначе если SumA < SumB, то вывести сообщение «сумма элементов главной и побочной диагоналей второй матрицы больше, чем первой», иначе вывести сообщение «сумма элементов главной и побочной диагоналей первой матрицы равна сумме элементов главной и побочной диагоналей второй матрицы».

Схема алгоритма 51.2

 

 

Алгоритмы ввода и вывода матрицы аналогичны алгоритмам ввода и вывода одномерного массива, использованным в предыдущих задачах, за исключением использования вложенных циклов.

Текст программы на языке Си

#include <stdio.h>

#include <stdlib.h>

/* Квадратные матрицы размера N*N представляются

динамическими массивами из N*N элементов с

доступом только с помощью указателей */

 

/*Ввод квадратной матрицы из N строк по N столбцов:

В подсказке используется имя матрицы MatrName

                            типа const char*

Функция выделяет память под массив из N*N элементов

типа double и заполняет его путем ввода значений

с клавиатуры. В случае ошибок возвращает NULL, иначе

указатель на выделенную область памяти */

double* InputRealQuadMatrix(int N,

                  const char* MatrName)

{

double *A=NULL;

int i,j;

if(N > 0){

if((A=malloc(N*N*sizeof(double)))==NULL)

    return NULL;

for(i=0; i<N; i++)

       for(j = 0; j < N; j++){

      printf("Введите %s[%d,%d]: ",MatrName,

                         i+1,j+1);

      scanf("%lf", A+i*N+j);

}

return A;

}

else

return NULL;

}

 

/* Вывод квадратной матрицы M размера N х N:

MatrName - выводимое на экран имя матрицы

                      (const char *)

 */

void OutputRealQuadMatrix(const char *MatrName,

                          double *M, int N)

{

int i,j;

for(i = 0; i < N; i++){

for(j=0; j< N; j++)

    printf("%s[%d,%d]=%8.3lg ",MatrName,i+1,

                            j+1,*(M+i*N+j));

printf("\n");

}

}

 

double sum_diag(double *A, int N){

double S = 0;

int i;

for(i=0; i < N; i++)

S = S + *(A+i*N+i) + *(A+i*N+N-i-1);

/*при i=0 A[i][N-i-1] -- верхний правый угол */

if(N % 2 == 1)

S = S-*(A+(N/2)*N+N/2);

return S;

}

 

int main(int argc, char *argv[]) {

int Na, Nb;

double *A, *B, SumA, SumB;

printf("Введите число строк матрицы A: ");  

scanf("%d",&Na);

A=InputRealQuadMatrix(Na,"A");

printf("Введите число строк матрицы B: ");

scanf("%d",&Nb);

B=InputRealQuadMatrix(Nb,"B");

printf("Исходная матрица A:");

OutputRealQuadMatrix("A",A,Na);

printf("Исходная матрица B:");

OutputRealQuadMatrix("B",B,Nb);

SumA = sum_diag(A, Na);

SumB = sum_diag(B, Nb);

if(SumA > SumB){

printf("Сумма элементов главной ");

printf("и побочной диагоналей ");

printf("первой матрицы больше, ");

printf("чем второй.");

}

else

if(SumA < SumB)

{

    printf("Сумма элементов главной ");

    printf("и побочной диагоналей ");

    printf("второй матрицы больше, ");

    printf("чем первой.");

}

else

{

    printf("Сумма элементов главной ");

    printf("и побочной диагоналей ");

    printf("первой матрицы равна сумме ");

    printf("элементов главной и побочной ");

    printf("диагоналей второй матрицы.");

}

if(A)

free(A);

if(B)

free(B);

system("pause");

return 0;

}

Вариант функции вывода матрицы в виде таблицы

void OutputRealQuadMatrixM(const char *Name,

                          double *M, int N)

{

int i,j;

if(Name)

printf("%s\n",Name);

for(i = 0; i < N; i++){

for(j=0; j< N; j++)

    printf("%8.3lg ",*(M+i*N+j));

printf("\n");

}

}