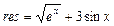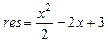Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 53. Использование вспомогательных алгоритмов. Передача функции как параметра в другую функцию. Нахождение площади между двумя кривымиСодержание книги
Поиск на нашем сайте
Условие задачи. Найти площадь между кривыми Из математики известно, что определенный интеграл
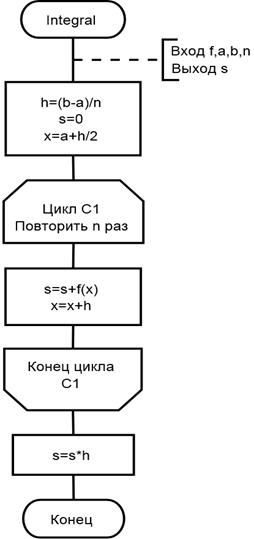
Рис. 3 Алгоритм приближенного вычисления интеграла методом прямоугольников был подробно рассмотрен в задаче 16. Интервал [ a; b ] разбивается на n равных отрезков, длина которых h =(b - a)/ n, и на каждом отрезке строится прямоугольник, высота которого равна значению подынтегральной функции в центре отрезка. Таким образом, площадь искомой криволинейной трапеции приближенно представляется суммой площадей полученных прямоугольников, т.е. В качестве подынтегральной функции может быть взята любая непрерывная на интервале [ a; b ] функция, вид этой функции никак не может повлиять на алгоритм. Следовательно, нет необходимости составлять алгоритм вычисления интеграла для каждой конкретной функции, достаточно имеющегося обобщенного алгоритма. Таким образом, можно сделать вывод, что данный алгоритм является вспомогательным для решения поставленной задачи. Чтобы с его помощью можно было вычислить значение определенного интеграла от конкретной функции на конкретном отрезке [ a; b ], эти данные ему нужно передать. Чтобы оба интеграла вычислялись с одинаковой точностью, число разбиений у них должно совпадать. Этого можно добиться двумя способами: или взять некоторое фиксированное значение n, или запросить его у пользователя в основной части алгоритма, и передать во вспомогательный. Выберем второй вариант. Итак, входными данными для алгоритма вычисления интеграла являются подынтегральная функция f (x), пределы интегрирования a и b (вещественные числа) и число разбиений n (натуральное число). Результатом работы алгоритма будет значение интеграла, это выходное данное. Входные данные будут передаваться в функцию вычисления интеграла из вызывающего алгоритма через параметры, а вычисленный результат будет непосредственно возвращаться в точку вызова. Структурированная запись вспомогательного алгоритма вычисления интеграла Integral Входные данные – функция f (x), вещественные числа a и b, целое n, результат – значение суммы s. 1. Получить от вызывающего алгоритма функцию f и значения a, b и n. 2. Вычислить шаг интегрирования 3. Повторять n разследующие действия: 3.1. Прибавить к сумме очередное слагаемое s= s+ f (x). 3.2. Вычислить новое значение x= x+ h. 4. Умножить на величину h полученную сумму s= s* h. 5. Передать вызывающему алгоритму значение s. Схема алгоритма
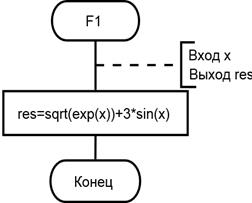
Подынтегральная функция, как и любая другая функция, – это тоже вспомогательный алгоритм, который производит вычисление значения заданного выражения при известном значении аргумента. В рассматриваемой задаче таких функций две, они выполняют вычисления по разным формулам, следовательно, они работают по разным алгоритмам. Но внешне эти функции схожи: у обеих одно входное данное – вещественное число х, и одно выходное данное – значение вычисленного выражения. Структурированная запись вспомогательного алгоритма F 1 Входное данное – вещественное число х, выходное данное – значение выражения res 1. Получить от вызывающего алгоритма значение х 2. Вычислить значение 3. Передать вызывающему алгоритму значение res. Схема алгоритма
Структурированная запись вспомогательного алгоритма F 2 Входное данное – вещественное число х, выходное данное – значение выражения res 1. Получить от вызывающего алгоритма значение х 2. Вычислить значение 3. Передать вызывающему алгоритму значение res. Схема алгоритма
Итак, определены три вспомогательных алгоритма: алгоритм вычисления интеграла и два алгоритма подынтегральных функций. Теперь нужно составить основной алгоритм, который, используя вспомогательные алгоритмы, будет решать поставленную задачу. Входными данными для него будут координаты концов отрезка a и b, а результатом – искомая площадь S. Значения a и b вводятся с клавиатуры, после этого можно вычислить значения интегралов от функций f 1(x) и f 2(x) и найти их разность по модулю. Полученное число и будет искомым значением площади. Чтобы использовать вспомогательный алгоритм, к нему нужно обратиться по имени, указав в скобках значения необходимых ему входных данных, в данном случае – имя подынтегральной функции, значения координат концов отрезка [ a; b ] и число разбиений n. Например, обращение Integral (F1, 1, 3, 100) приведет к тому, что начнет выполняться вспомогательный алгоритм с именем Integral и обозначения, используемые в нем, будут применяться к данным, указанным в скобках: f станет обозначать вспомогательный алгоритм F 1, a – число 1, b – число 3, а n – число 100. Соответственно использованное в алгоритме Integral обращение f (x) будет тождественно обращению F 1 (x).
|
|||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.247.24 (0.007 с.) |

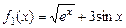 и
и 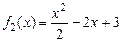 на отрезке от а до b как разность интегралов
на отрезке от а до b как разность интегралов 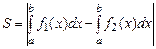 .
.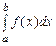 равен площади криволинейной трапеции – фигуры, ограниченной сверху графиком положительной на отрезке [ a; b ] функции y = f (x), слева прямой x = a, справа прямой x = b, и снизу осью ОХ. Вычислить значение определенного интеграла можно для любой непрерывной на отрезке [ a; b ] функции. Следовательно, площадь искомой фигуры будет равна разности площадей криволинейных трапеций, ограниченных прямыми x = a, x = b, y =0 и графиками функций f 1(x) и f 2(x), то есть абсолютного значения разности интегралов
равен площади криволинейной трапеции – фигуры, ограниченной сверху графиком положительной на отрезке [ a; b ] функции y = f (x), слева прямой x = a, справа прямой x = b, и снизу осью ОХ. Вычислить значение определенного интеграла можно для любой непрерывной на отрезке [ a; b ] функции. Следовательно, площадь искомой фигуры будет равна разности площадей криволинейных трапеций, ограниченных прямыми x = a, x = b, y =0 и графиками функций f 1(x) и f 2(x), то есть абсолютного значения разности интегралов 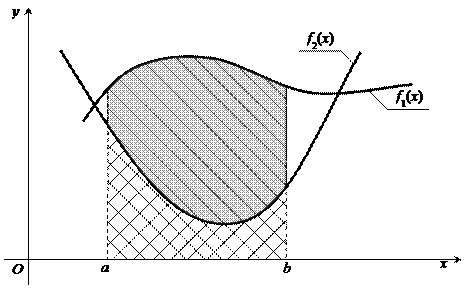
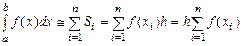 , где x 1= a + h /2, а остальные xi = xi -1+ h. Чем больше значение n, тем точнее вычисляется интеграл.
, где x 1= a + h /2, а остальные xi = xi -1+ h. Чем больше значение n, тем точнее вычисляется интеграл.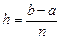 . Обнулить значение суммы s=0 и задать начальное значение
. Обнулить значение суммы s=0 и задать начальное значение 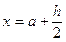 .
.