
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Начальные отрезки вполне упорядоченного множестваСодержание книги
Поиск на нашем сайте
Определение 7.1. X+=A(a) Множество A(a) называется начальным отрезком вполне упорядоченного множества, определяемым элементом a этого множества. Таким образом, начальный отрезок A(a) – множество всех элементов множества A+, предшествующих в данном множестве элементу a, причем элементы начального отрезка A(a) упорядочены в нем так же, как и в множестве A+. Из определения 7.1 и теоремы 6.1 следует: Следствие 7.1. Произвольный начальный отрезок вполне упорядоченного множества есть вполне упорядоченное множество. Заметим еще, что начальный отрезок, определяемый первым элементом вполне упорядоченного множества A +, есть пустое множество. Определение 7.2. a1, A2 Определяемое отношение будем называть отношением «меньше». Поле этого отношения есть множество всех начальных отрезков данного вполне упорядоченного множества. Теорема 7.1. Отношение, сопоставляющее любому элементу a множества начальный отрезок A (a), устанавливает подобие множества A + и множества всех его начальных отрезков, упорядоченных отношением «меньше». Доказательство самостоятельно. Из теоремы 7.1 и следствия 6.1 непосредственно следует: Следствие 7.2. Множество всех начальных отрезков множества A +, упорядоченное отношением «меньше», есть вполне упорядоченное множество. Лемма 7.1. A+ Доказательство. Допустим, что отношение R устанавливает подобие множеств A+ и B+ и что a – произвольный элемент множества A. Будем считать также, что b=R (a). Легко видеть, что A(a) Таким образом, лемма верна. В определение, которое мы ниже сформулируем, входит символ YX. Определение данного символа – это определение 8.3 предыдущего раздела. (R Определение 7.3. R Выражение R Лемма 7.2. R Таким образом, возрастающая функция, определенная на некотором множестве, не может сопоставлять ни одному элементу множества предшествующий элемент данного множества. Доказательство. Пусть – вопреки тому, что требуется доказать, - для некоторого a (1) R(a) Обозначим через Поэтому множество (2) R(a0) а также для любого x (3) x Полагая, что x=R(a0), получаем из формул (2) и (3) (4) ~[R(R(a0)) С другой стороны, из формулы (2) и допущения, что функция R возрастающая, получаем R(R(a0)) Но данная формула противоречит формуле (4). Таким образом, допущение (1) приводит к противоречию. Лемма 7.3. ~[A+ Таким образом, вполне упорядоченное множество не подобно ни одному из своих начальных отрезков. Доказательство. Пусть, вопреки тому, что требуется доказать, - для некоторого a1 (1) A+ Обозначим через R отношение, устанавливающее подобие этих множеств. Из определения 2.4 мы получаем (2) x Отношение R есть поэтому возрастающая функция, определенная на множестве A+. Отсюда и из леммы 7.2 следует, что (3) ~[R(a1) Но, с другой стороны, из того, что A+ Таким образом, допущение (1) приводит к противоречию. Следовательно исходная формулировка леммы верна. Лемма 7.4. a1, a2 Доказательство. Допустим, что a1 ~[A(a1)] Таким образом лемма верна. Лемма 7.5.
Таким образом, если для любого начального отрезка множества A + существует подобные ему начальный отрезок множества B + и обратно, то множества A + и B + подобны. Доказательство. Покажем, что подобие множеств A+ и B+ устанавливает отношение R, определяемое эквивалентно (1) aRb Из условий леммы и формулы (1) легко следует (2) Dℓ(R)=A, DP(R)=B Допустим, что aRb1 и aRb2. Отсюда и из формулы (1) следуют формулы: A(a) A(a) В свою очередь отсюда и из теоремы 2.1 b,c следует, что B(b1) На основании леммы 7.4 мы замечаем, что b1= b2. Сходным образом можно показать, что из допущений a1Rb и a2Rb следует, что a1=a2. Поэтому отношение R взаимнооднозначно. Отсюда и из формул (2) следует (3) A ~R B. Допустим теперь, что (4) a1 а также, что (5) a1Rb1 и a2Rb2. Из формул (1) и (5) следует: (6) A(a1) (7) A(a2) Из формулы (4) легко следует, что a1 (8) b' (9) A(a1) Из формул (6) и (9) выводим, что B(b1) Следовательно, по лемме 7.4 b1= b'. Отсюда и из формулы (8) следует, что b1 (10) b1 Из того, что из формул (4) и (5) мы получили (10), а также из (3) следует утверждение леммы. Лемма 7.6. Если в0 – первый элемент множества B+ , удовлетворяет условию 1) и если а1 2) Доказательство. пусть – вопреки тому, что требуется доказать, - 2)
Однако эта формула противоречит первому условию леммы. Поэтому допустим, что Данное заключение опять-таки противоречит первому условию леммы. Таким образом, косвенное доказательство леммы закончено. Лемма 7.7. Доказательство. Пусть вопреки тому, что требуется доказать, - существует такой элемент (1) а также существует такой элемент (2) обозначим через а0 первый элемент множества А+, удовлетворяющий условию (1); через b0 – первый элемент множества В+, удовлетворяющий условию (2). Допустим, что a1 Отсюда и из леммы 7.6, мы заключаем, что b1 Таким образом, мы показали, что (3)
Сходным образом можно показать, что (4) Из формул (3) и (4), а также леммы 7.5 следует, что A(a0) Таким образом, косвенное доказательство леммы закончено. Теорема 7.2. A+ Таким образом, два вполне упорядоченных множества или подобны, или одно из них подобно начальному отрезку другого. Доказательство. Из леммы 7.7 следует, что выполняется хотя бы одно из следующих условий: (1) (2) Если выполняется оба эти условия, то по лемме 7.5 (3) A+ Допустим теперь, что выполняется условие (1), но не выполняется условие (2), а потому существует элемент в множестве B+, удовлетворяющий соотношению:
Обозначим через b0 первый элемент множества B+, удовлетворяющий данному соотношению. Будем также считать, что (4) C+=B(b0). Из определения элемента b0 и формулы (4) легко следует (5) Пусть a1 A(a1) Отсюда и из леммы 7.6 следует, что b1 Таким образом, мы показали, что (6) Из леммы 7.5 формул (5), а также (6) следует, что A+ Отсюда из формулы (4) получаем (7) A+ Сходным образом можно показать, что для некоторого a0 (8) B+ Значит, хотя бы одна из формул (3), (7), (8) верна. Таким образом, теорема 7.2 доказана. Лемма 7.8. Доказательство. Пусть отношение R устанавливает подобие множеств Из третьего условия леммы следует существование такого элемента b' множества B, что (1) A+ Пусть b1 – элемент множества B1 удовлетворяющий условию: b1= Отсюда и из замечания, что отношение (2) B(b') Из первого условия леммы, формул (1) и (2), а также из замечания, что отношение
Отсюда уже следует утверждение леммы. Теоремами и леммами, доказанными в этом параграфе, будем пользоваться в следующем параграфе.
|
||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 71; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.255.135 (0.007 с.) |

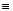 X+
X+ 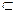 A+
A+ 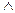
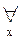 (x
(x 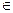 X
X 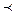 A a).
A a).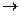 [A(a1)< A(a2)
[A(a1)< A(a2) 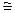 B+
B+ 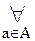
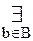 [A(a)
[A(a) 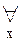
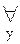 [x
[x 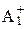 подмножество множества A+;
подмножество множества A+; 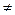 a2. Отсюда из леммы 7.3 и замечания, что из двух (различных) начальных отрезков одного и того же упорядоченного множества один есть всегда начальный отрезок другого, следует
a2. Отсюда из леммы 7.3 и замечания, что из двух (различных) начальных отрезков одного и того же упорядоченного множества один есть всегда начальный отрезок другого, следует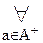
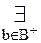 [A(a)
[A(a) 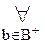
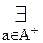 [A(a)
[A(a) 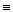 A(a)
A(a) 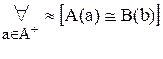
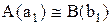 , то
, то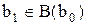
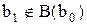 . Отсюда следует, что или b0= b1, или b0<Bb1. В первом случае формула (2) принимает вид:
. Отсюда следует, что или b0= b1, или b0<Bb1. В первом случае формула (2) принимает вид: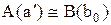
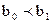 . Отсюда и из леммы 7.1 и условия (2) следует существование элемента а` множества А(а1), такого, что
. Отсюда и из леммы 7.1 и условия (2) следует существование элемента а` множества А(а1), такого, что 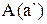
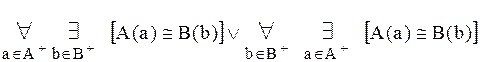
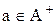 , что
, что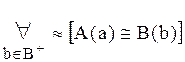
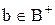 , что
, что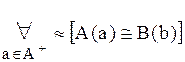
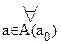
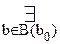 [A(a)
[A(a) 
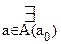 [A(a)
[A(a) 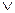
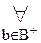
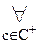

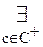 [A(a)
[A(a) 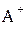
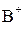
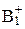
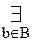 [A+
[A+ 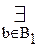 [
[ 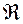 (b').
(b').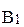 (b1)
(b1)


