Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подобные множества. Порядковые типы.
Теория упорядоченных множеств во многих отношениях аналогична общей теории множеств, которой был посвящен предыдущий раздел. Например, содержание этого параграфа аналогично содержанию §7 раздела II. Сначала приведем несколько простых вспомогательных определений. Определение 2. 1.
b)
Определенные выражения читаются: а) отношение R связано в множестве А; b) отношение R транзитивно в множестве А; с) отношение R асимметрично в множестве А. Таким образом, каждый из символов: св(А), транз(А), асим(А) - обозначает некоторое множество отношений, зависящих от А. Дальнейшие определения имеют уже основное значение для теории упорядоченных множеств. Определение 2.2.
Определяемое выражение читается: отношение R упорядочивает множество А. Поэтому для того, чтобы некоторое отношение упорядочивало множество А, необходимо и достаточно выполнения следующих условий: Множество А – поле отношений R и R связно, транзитивно и асимметрично в этом множестве. 1) Типичными отношениями, упорядочивающими множество действительных чисел, являются отношения «меньше» и «больше»; 2) Типичны и два следующих отношения: t1 раньше t2, t1 позже t2, которые упорядочивают произвольное множество моментов времени. Определение 2.3.
Таким образом, упорядоченные множества – это пары, первые элементы которых произвольные множества, а вторые – отношения, упорядочивающие данные множества. Для того, чтобы выяснить содержательный смысл определения 2.3, элементы х и у множества А, удостоверяющие условию «хRу», мы договоримся называть: х – предшествующим элементом, а у – следующим элементом. Теперь мы можем выразить определение 2.3 в следующей нестрогой, но зато содержательно ясной форме: Множество упорядочено тогда и только тогда, когда: а) для любых двух (различных) элементов рассматриваемого множества установлено, который из них предшествующий и который из них последующий (условие связности); причем b) если элемент х предшествует у и у предшествует z, то х предшествует z (условие транзитивности); с) ни один элемент х не может быть предшествующим и одновременно следующим по отношению к элементу у (условие асимметричности). Примерами упорядоченных множеств являются пары: áÂ, <ñ, áÂ, >ñ, áN, <ñ, áN, >ñ. (Заметим, что в соответствии с отношением, введенным в §1 и относящимся к символам типа áХ, Rñ отношения “<” и “>” ограничены здесь множеством  (множество  - поля этих отношений)).
Из аксиомы 1.4 предыдущего раздела следует, что упорядоченные множества áÂ, <ñ и áÂ, >ñ. Различны, так как отношения «меньше» и «больше», очевидно, различны (сравните определение 6.10, раздел II). Введем теперь некоторые терминологические отношения и некоторые упрощения принятой символики. Согласимся прежде всего называть множество А запасом упорядоченного множества áА, Rñ. Заметим далее: о предмете α мы говорим, что α есть элемент упорядоченного множества тогда, и только тогда, когда α есть элемент запаса данного множества, то есть αÎА. В качестве обозначения того, что a принадлежит áА, Rñ, мы пишем: αÎáА, Rñ. Таким образом, имеет место следующая эквивалентность:
Символ Î употребляется здесь в двух различных смыслах: в одном случае (αÎáА, Rñ) он обозначает принадлежность предмета упорядоченному множеству, а в другом – (aÎА) – принадлежность неупорядоченному множеству. Однако из контекста всегда будет ясно, в каждом из этих смыслов употребляется символ Î. При рассмотрении упорядоченных множеств часто фиксируется, какое отношение упорядочивает данное множество, или же бывает безразлично, каково это отношение. В последнем случае, так как когда безразлично какое отношение упорядочивает данное множество А, вместо того, чтобы пользоваться символом áА, Rñ, будем пользоваться символом Ао. Таким образом символы Ао, Во, Со,…..обозначают упорядоченные множества, имеющие запасы А, В, С…. Очевидно, что если в какой-либо формуле или доказательстве несколько раз повторяется символ Ао, то каждый раз этот символ обозначает множество, упорядоченное одним и тем же отношением. Еще одно соглашение: в качестве обозначения того, что элементы х и у множества <А, R> удовлетворяют условию «хRу», будем писать: 1) Это отношение читается: элемент х предшествует в множестве Ао элементу у. Таким образом, имеет место следующая эквивалентность:
Заметим, что в выражении 1) мы иногда будем опускать индекс А. а) b) c) Следующее определение – аналог определения 2.1 раздела I: Определение 2.4.
Выражение Другое условие, которому должно удовлетворять отношение R, можем выразить так: элементы множества Во, сопоставленные отношением R элементам х и у множества Ао, находятся в множестве Во в том же отношении порядка, в каком находятся элементы х и у в множестве Ао. Определение 2.4 можем записать также в следующем виде:
Обозначим через С1 множество отрицательных целых чисел. Легко видеть, что отношение R1, определяемое эквивалентностью
устанавливает подобие множеств áN,<ñ, áС1,>ñ. Определяемое отношение читается: упорядоченные множества Ао и Во подобны. Это отношение – аналог отношения равночисленности множеств (сравните определение 1.2, раздел II). Очевидно, что понятие подобия упорядоченных множеств – частный случай изоморфизма. Из определений 2.5 и 2.4 следует: Следствие 2.2.
Таким образом, запасы подобных множеств равночисленны. Обратная импликация не имеет места, потому что, например, множества áN,<ñ, áN1,>ñ, очевидно, не подобны. Теорема 2.1. а) b) c) Таким образом, отношение подобия множеств есть отношение типа эквивалентности. Доказательство. Теорема 2.1 – аналог теоремы 7.1 раздела I. Доказательства этих теорем также сходы. Поэтому мы ограничимся следующими краткими замечаниями: В доказательстве формулы теоремы 2.1(а) следует воспользоваться отношением тождества, ограниченным множеством А; 1) если отношение R устанавливает подобие множеств Ао и Во, то и отношение R-1 устанавливает подобие множеств Во и Ао; 2) если отношение R устанавливает подобие множеств Ао и Во, а отношение S – подобие множеств Во и Со, то относительное произведение этих отношений устанавливает подобие множеств Ао и Со. Введем новое исходное понятие, аналогичное понятию мощности множеств. Это понятие порядкового типа упорядоченного множества. Порядковый тип множества Ао. Порядковый тип множества Ао обозначается через Āо. По Кантору, который был создателем не только общей теории множеств, но и теории упорядоченных множеств, к понятию порядкового типа данного множества мы приходим, отвлекаясь от того, какие предметы образуют данное множество. Черточка в обозначении порядкового типа и должна символизировать собственно эту единственную абстракцию. Смысл введенного понятия раскрывается в следующей аксиоме, аналогичной аксиоме 7.1 раздела I: Аксиома 2.1. Ао=ВоºАо@Во Таким образом, порядковые типы двух упорядоченных множеств тождественны тогда, и только тогда, когда эти множества подобны. Заметим, что из аксиомы 2.1 непосредственно следует теорема 2.1.
Выражение aÎПТ читается: a есть порядковый тип. Произвольные порядковые типы будем обозначать малыми буквами греческого алфавита. Из определения 2.6 следует а) b) c) Определение 2.6 и теорема 2.2 – аналоги определения 7.3 и теоремы 7.2 раздела I. Из аксиомы 7.1 раздела I Следствие 2.3.
Обратная импликация не имеет места, что можно подтвердить примером Ао=áÂ,<ñ и Во=áÂ,>ñ. В последней части §7 предыдущего раздела мы заметим, что значительное большинство теорем о мощностях множеств можно сформулировать без использования этого понятия, ограничившись понятием равночисленности множеств. Сходным образом теоремы о порядковых типах можно заменить теоремами, в которые входят понятие подобия множеств. Таким образом, исключение из списка исходных понятий теории множеств понятия порядкового типа (с одновременным исключением аксиомы 2.1) не привело бы к существенному обеднению этой теории подобно тому, как не вызывает существенного ее обеднения исключение понятия мощности. Следующей леммой, аналогичной лемме 7.4 предыдущего раздела, будем пользоваться многократно. Лемма 2.1. Для любых упорядоченных множеств Ао и Во существуют такие порядковые множества Ао1 и Во1, что Ао1~Ао, Во1~Во и А1·В1=0. Доказательство. Множества А1 и В1 мы определим так:
Мы принимаем также, что
Легко видеть, что так определенные упорядоченные множества Ао1 и Во1 удовлетворяют требуемым условиям. При рассмотрении порядковых типов безразлично, какое из подобных множеств мы принимаем во внимание. По лемме 2.1 мы можем всегда данные два множества заменить непересекающимися множествами.
|
|||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.22.136 (0.021 с.) |
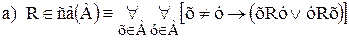





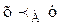

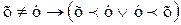
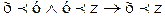


 читается: отношение R устанавливает подобие упорядоченных множеств Ао и Во. Таким образом, для того, чтобы отношение R устанавливало подобие множеств, необходимо выполнение следующего условия: R устанавливает равночисленность запасов этих множеств, а потому R взаимооднозначно и Dℓ(R)=А, Dp(R)=B.
читается: отношение R устанавливает подобие упорядоченных множеств Ао и Во. Таким образом, для того, чтобы отношение R устанавливало подобие множеств, необходимо выполнение следующего условия: R устанавливает равночисленность запасов этих множеств, а потому R взаимооднозначно и Dℓ(R)=А, Dp(R)=B.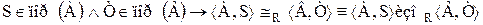


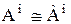
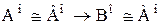
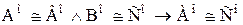
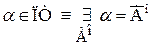


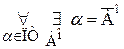
 , а также следствия 2.2
, а также следствия 2.2  и аксиомы 2.1
и аксиомы 2.1  легко следует
легко следует