Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Канторовское доказательство существования
Трансцендентных чисел.
В высшей алгебре алгебраическими числами называют те, и только те комплексные числа, которые являются корнями многочленов с целыми коэффициентами. Комплексные числа, которые не являются алгебраическими, называются трансцендентными. Существование трансцендентных чисел было впервые доказано французским математиком Лиувиллем в 1851 г. В 1873 г. Кантор показал, что множество всех трансцендентных чисел имеет мощность контилиума. Мы приведем это доказательство в качестве примера классического решения математической проблемы методом теории множеств. Лемма 13.1. Множество всех действительных алгебраических числе счетно. Доказательство. Из теоремы 12.10 легко следует, что множество многочленов с целыми коэффициентами счетно. Отсюда и из того, что любой многочлен имеет конечное число действительных корней, из леммы 12.3 и из того, что множество всех действительных алгебраических чисел бесконечно (так как любое рациональное число есть алгебраическое число), легко следует лемма. Теорема 13.1. Множество всех действительных трансцендентных чисел имеет мощность континиума. Доказательство. Теорема есть непосредственное следствие из теоремы 12.2 и леммы 13.1. Аксиома выбора. В 1904 г. Э.Цермело (нем.) сформулировал аксиому, называемую аксиомой выбора. Аксиома 14.1.
Проводим словесную формулировку этой аксиомы: Пусть Z – семейство множеств, такое, что: 1) Z – непусто; 2) каждое множество, принадлежащее Z, также непусто; 3) любые два (различные) множества, принадлежащие семейству Z, не пересекаются. По аксиоме Цермело, в этих условиях существует не менее одного множества У, имеющего с каждым множеством М Î Z единственный общий элемент. В качестве примера доказательства, где используется аксиома 14.1, приведем доказательство следующей аксиомы, которую мы упоминали в §11. Теорема 14.1. По этой теореме, произвольное непустое множество, мощность которого отлична от любого набуренного числа, содержит счетное подмножество, а потому – в соответствии с теоремой 11.1 – бесконечное в смысле Дедекинда. Доказательство. Пусть m – произвольное натуральное число. Обозначим через С(m) множество всех m – элементных последовательностей, члены которых – различные элементы множества Х. Покажем с помощью индукции, что для произвольного натурального k множество С(k) непусто.
По условию множество Х непусто. Поэтому существует элемент х1Î Х. Последовательность, единственный член, который есть х1, принадлежит множеству С(1). Таким образом, множество С(1) – непусто. Пусть k – произвольное натуральное число. Допустим, что для k выполняется доказываемое свойство множеств. Поэтому существует последовательность (1) С1, С2 ……… Сk члены которой – различные элементы множества Х. Если бы в множестве Х не существовало элемента, отличного от любого числа последовательности (1), то мощность множества Х равнялась бы числу k. Но это заключение противоречит второму условию доказываемой теоремы. Таким образом, существует элемент множества Х, отличный от любого числа последовательности (1). Обозначим этот элемент через Сk +1. Последовательность: С1, С2 ……… Сk, Сk +1 принадлежит, очевидно, множеству С(k + 1). Поэтому данное множество непусто. Очевидно также, что при i = j: С(i) · С(j) = 0. Множества: (2) С(1), С(2), С(3), …. удовлетворяют, таким образом, условиям аксиомы 14.1. Следовательно, существует множество С, которое с каждым из множеств (2) имеет единственный общий элемент. Пусть последовательность Вычеркнем в последовательности С1(1), С1(2) , С2(2), С1(3), С2(3), С3(3), С1(4) … Каждый член, для которого в данной последовательности существует предшествующий и равный ему член. Обозначим через {уn} полученную таким путем последовательность. Допустим временно, что эта последовательность конечна и насчитывает r элементов. Очевидно, тогда в последовательность Однако это заключение противоречит определению последовательности {уn}. Поэтому данная последовательность бесконечна. Очевидно также, что члены этой последовательности – различные элементы множества Х. Таким образом, теорема 14.1 верна. Заметим, что без аксиомы 14.1 из условий теоремы 14.1 мы могли бы вывести лишь то, что для любого натурального числа n существует n – элементная последовательность, члены которой – различные элементы множества Х. Однако мы не могли бы показать существование бесконечной последовательности, обладающей этим свойством.
Аксиома выбора, пожалуй, - чаще всего оспариваемая в математике аксиома. Это вызвано тем, что, с одной стороны, на основании данной аксиомы доказывают вполне очевидные теоремы, которые нельзя доказать без данной аксиомы (например, теорема 14.1), а с другой стороны, тем, что среди следствий этой аксиомы имеются парадоксальные теоремы, не соответствующие содержательным представлениям. Отсюда же среди математиков, и притом очень видных, можно найти как сторонников, так и противников принятия аксиомы выбора. Уже в 1902 г. Белло Леви обратил внимание на то, что доказательство теоремы: «Множество суммы семейства непересекающихся и непустых множеств больше или равно мощности этого семейства» требует возможности выбрать по одному элементу из каждого множества этого семейства. Сходным образом введение определения суммы бесконечной последовательности кардинальных чисел (обобщение определения суммы двух кардинальных чисел) предполагает аксиому выбора, как заметил В.Серпинский в работе 1918 г. об этой аксиоме. Такая же ситуация имеет место и в определении произведения бесконечной последовательности кардинальных чисел и других операций на кардинальных числах, а также порядковых типах и числах, о которых речь будет идти в разделе II, при распространении определений этих операций на бесконечное множество элементов. Из данных примеров видно, что уже при введении относительно элементарных понятий теории множеств необходимо обращаться к аксиоме выбора. Также и в других разделах математики, например, в анализе, алгебре, топологии аксиома выбора (или ее частные случаи, или же эквивалентные ей теоремы) необходима для доказательства теорем, истинность которых не вызывает сомнений. Из многочисленных примеров такого рода мы приведем один. В анализе известны два определения непрерывности функции f (х) в точке хо. В данном определении содержание данного понятия раскрываются через условие: (а) А в другом – через условие (b) И вот в доказательстве эквивалентности этих определений, а именно в доказательстве того, что из (b) следует (а), необходимо обратиться к аксиоме выбора. Отрицательное отношение к аксиоме выбора вызвано, главным образом, двумя мотивами: 1) с помощью этой аксиомы доказывается существование предметов некоторого рода, хотя не удается указать ни одного примера такого предмета (так называемые неэффективные доказательства существования); 2) с помощью этой аксиомы доказываются содержательно неочевидные теоремы (в частности, некоторые геометрические теоремы), из которых наиболее известна теорема Банаха-Тарского о парадоксальном разложении шара (см. приложение). Известны многочисленные теоремы, которые эквивалентны аксиоме выбора на основании остальных аксиом теории множеств. Одна из таких теорем – закон трихотомии для кардинальных чисел: m<n Проблема независимости аксиомы выбора от остальных аксиом теории множеств не решена до сих пор (имеется лишь доказательство независимости для такой аксиоматики, в которой принимается существование бесконечного числа предметов, отличных от множеств).
Лишь в частном случае, когда семейство Z, о котором говорится в аксиоме 14.1, конечно, удастся доказать аксиому 14.1. Именно сначала доказывается это утверждение для случая, когда Z = {Х1}, следующим образом: По условию аксиомы 14.1 мы имеем: (1) (2) (3) (4)
Затем индукцией доказывается это же утверждение для случая, когда
|
|||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 77; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.26.176 (0.017 с.) |


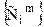 - единственный общий элемент множеств С и С(m).
- единственный общий элемент множеств С и С(m).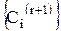 обязательно войдет хотя бы один член, отличный от каждого члена последовательности {уn}.
обязательно войдет хотя бы один член, отличный от каждого члена последовательности {уn}.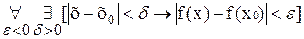



 m=n
m=n 
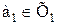 {1}
{1} {2}
{2}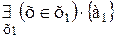 {3}
{3} {4}
{4} . Однако если семейство Z счетно, то аксиому 14.1 не удается доказать уже для случая, когда элементы семейства Z – двухэлементные множества.
. Однако если семейство Z счетно, то аксиому 14.1 не удается доказать уже для случая, когда элементы семейства Z – двухэлементные множества.