
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вполне упорядоченные множества. Порядковые числа.
Определение 6.1. Упорядоченное множество A 0 есть вполне упорядоченное множество Таким образом, множество вполне упорядочено тогда, и только тогда, когда каждое его непустое подмножество имеет первый элемент. Из определения 6.1. и леммы 5.1. непосредственно следует, что любое конечное упорядоченное множество вполне упорядочено. Множество á однако ни áB ни áR не относятся к вполне упорядоченным множествам. Из теоремы 4.2а легко следует: Следствие 6.1. Множество, подобное вполне упорядоченному множеству, также вполне упорядочено. Определение 6.2. α Выражение α Таким образом, порядковые числа – это порядковые типы вполне упорядоченных множеств.
Заметим далее, что если рассматривать натуральные числа как порядковые типы конечных множеств (см. замечания предыдущего параграфа), то натуральные числа будут частными случаями порядковых чисел. Также и число 0, понимаемое как порядковый тип пустого множества по определениям 6.1 и 6.2 есть порядковое число. Теорема 6.1. Любое подмножество вполне упорядоченного множества вполне упорядочено. Доказательство. Пусть B0 – произвольное подмножество вполне упорядоченного множества A0, а C0 – произвольное непустое подмножество множества B0. Легко видеть, что множество C0 есть подмножество множества A0. Поэтому множество C0 имеет первый элемент. Таким образом, мы показали, что любое непустое подмножество множества B0 имеет первый элемент. Отсюда и из определения 6.1 следует, что данное множество вполне упорядочено. Теорема 6.2. Сумма и произведение вполне упорядоченных множеств – вполне упорядоченные множества. Доказательство. Пусть A0 и B0 – произвольные вполне упорядоченные множества и пусть C0 – произвольное непустое подмножество множества A0 + B0.
Если A×C Легко видеть, что данный элемент есть одновременно и первый элемент подмножества C0. Если же A×C=0, то множество C0 – есть подмножество вполне упорядоченного множества B0 и потому имеет первый элемент. Тем самым мы показали, что в обоих возможных случаях произвольное непустое подмножество множества A0+B0 имеет первый элемент. Таким образом, множество A0 + B0 вполне упорядочено. Пусть теперь C0 – произвольное непустое подмножество множества A0×C0. Обозначим через Аналогично определяется Легко видеть, что Пусть a0 и b0 будут соответственно первыми элементами этих множеств. Очевидно, что пара áa0,b0ñ есть первый элемент множества C0. Таким образом, множество A0×B0 также вполне упорядочено. Из доказанной теоремы следует, что операции на порядковых числах мы можем определить как частные случаи соответственных операций на порядковых типах. Отсюда непосредственно следует, что теоремы арифметики порядковых типов, доказанные в §3, остаются верными и в арифметике порядковых чисел. Заметим еще, что законы коммутативности сложения и умножения не имеют места не только для порядковых типов, но и для порядковых чисел. Это можно видеть из следующих неравенств: w+1 w несложное доказательство которых сделать самим. Заметим еще, что вполне упорядоченное множество с запасом A мы будем обозначать A+.
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 101; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.193.232 (0.007 с.) |
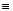
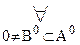
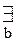 (b – есть первый элемент множества B 0).
(b – есть первый элемент множества B 0).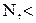 ñ - вполне упорядочено,
ñ - вполне упорядочено, ñ (B – рациональные числа)
ñ (B – рациональные числа)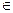 ПЧ
ПЧ  (A 0 есть вполне упорядоченное множество
(A 0 есть вполне упорядоченное множество 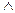 α = A 0).
α = A 0). Из предыдущих замечаний и следствий 5.2-5.4 следует, что из порядковых типов w,
Из предыдущих замечаний и следствий 5.2-5.4 следует, что из порядковых типов w, 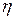 и
и 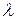 только w есть порядковое число.
только w есть порядковое число.
 w=á
w=á 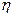 =áB
=áB 
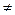 0, то мы можем принять, что элементы множества D0, запас которого есть множество A×C, упорядочены так же, как и в множестве A0. очевидно, что множество D0 – непустое подмножество вполне упорядоченного множества A0, а потому имеет первый элемент.
0, то мы можем принять, что элементы множества D0, запас которого есть множество A×C, упорядочены так же, как и в множестве A0. очевидно, что множество D0 – непустое подмножество вполне упорядоченного множества A0, а потому имеет первый элемент.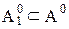 , элементы которого – те, и только те элементы множества A0, которые относятся к первым элементам упорядоченных пар, принадлежащих множеству C.
, элементы которого – те, и только те элементы множества A0, которые относятся к первым элементам упорядоченных пар, принадлежащих множеству C. .
.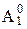
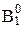
 2
2 


