
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Арифметика кардинальных чисел.
Определим сложение, умножение и возведение в степень кардинальных чисел. Для обозначения каждой из этих операций мы будем пользоваться символами, которые обозначаются в арифметике «обычных» чисел, например, в арифметике натуральных чисел или в арифметике действительных чисел. Мы сохраним также терминологию этих арифметик, называя, например, результат сложения кардинальных чисел − суммой, а складываемые кардинальные числа − слагаемыми. Определение 8.1. X∙Y = 0 → Это сокращенная форма определения сложения кардинальных чисел. Точная форма такого определения следующая: m+n = f ≡ Определения остальных операций мы приведем только в сокращенной форме. Определение 8.2.
Сформулируем вспомогательное определение: Определение 8.3.
Выражение читается: Из определения 8.3 следует: А~A1 Доказательство (*) аналогично лемме 7.5а. Из определения 8.3 легко следует также: Следствие 8.1.
Определение 8.4.
Таким образом мощность множества Х, возведенная в степень, равную мощности множества Y в множество X. Покажем, что определение 8.1− корректное определение. С этой целью нужно доказать, что для любых двух кардинальных чисел m и n существует только одно кардинальное число, равное их сумме. По теореме 7.2ссуществует такие множества А и А1, что Существование кардинального числа f Следовательно, для любых двух кардинальных чисел существует их сумма. Пусть теперь В и В1 – произвольные множества, удовлетворяющие условиям:
Из леммы 7.5 легко следует, что А + А1 ~ В + В1. Отсюда и из аксиомы 7.1 следует, что f=f1. Таким образом, существует единственная сумма данных кардинальных чисел. Аналогично можно показать корректность определения остальных операций. Покажем теперь, что операции на натуральных числах – это частные случаи операций на кардинальных числах. Пусть X = {x1, x2, …, xm}, Y = {y1, …, yn}. Предположим, что среди элементов x1, x2, …, xm нет тождественных, а также, что среди y1, …, yn нет тождественных элементов. Тогда Допустим далее, что каждый элемент множества Х отличен от каждого элемента множества Y. Очевидно,
Таким образом, сложнее натуральных чисел – частный случай множеств кардинальных чисел. Покажем, что (1) x1, x2, …, xm, члены которой – элементы множества Х. (Очевидно, что члены последовательности (1) с различными индексами могут быть тождественны.) Легко видеть, что таких последовательностей mn. Таким образом, и возведение в степень натуральных чисел – частный случай возведения в степень кардинальных чисел. В качестве примеров мы приведем теорему арифметики кардинальных чисел. Теорема 8.1. а. b. Эту теорему можно записать в таком виде: а) m+n = n+m b) m∙n = n∙m Доказательство. a. По лемме 7.4 мы можем считать, что множества X и Y не пересекаются. Тогда имеет место равенство (1): (1) X∙Y = Y∙X = 0 (2) (3) (4) (5) b. По определение 8.2имеют место следующие равенства:
Определим отношение, которое потребуется дальше в доказательстве: áz, tñ, R, áx, yñ ≡ x = t Очевидно, что (2) Из (1) и (2) следует:
Теорема 8.2.
Доказательство. По лемме 7.4мы можем считать, что равенство (1) имеет место: (1) X∙Y = 0 (2) (3) (4) (5) (6) (7)
Теорема 8.3.
Доказательство. Пусть Â1={1, 2, …, n}. Отсюда Â1=n. Обозначим через Xi (i = 1, 2, …, n) декартово произведение одноэлементного множества {i} и множества Х. Легко видеть, что имеют место следующие равенства:
Из этих формул, теоремы 5.1си определений 8.1 и 8.2следуют равенства: Таким образом, теорема верна. Теорема 8.4.
Доказательство. Пусть Â1={1, 2, …, n}. Отсюда Â1=n. Из определения 8.3следует, что множество ХÂ1 есть подмножество всех последовательностей х1, х2, …, хn, члены которых – элементы множества Х, а по определению 5.1множество Отсюда и из определений 8.2 и 8.4следует теорема. Теорема 8.5.
Доказательство, которое здесь приводится, содержит много сокращений. Доказательство. По лемме 7.4можем считать, что: (1) Y∙Z = 0. Пусть R – произвольная функция, отображающая множество Y+Z в множество Х. Отсюда и из формулы (1), а также определений 6.7 и 8.3 следуют формулы: RY RZ Пусть отношение S сопоставляет функции R упорядоченную пару <RY, RZ>. Отношение S устанавливает равночисленность множеств XY+Z и XY∙XZ. Отсюда уже легко следует теорема. Следующую теорему приведем без доказательства: RY Теорема 8.6.
Теоремы арифметики кардинальных чисел, которые приведены в этом параграфе, аналогичны теоремам арифметики натуральных чисел. Однако в дальнейших параграфах мы познакомимся с теоремами, не имеющими этого свойства. Заметим еще, что не было надо определений обратных операций: вычитания и деления. Причины, по которым в теории множеств эти операции не определяются, также будут выяснены в дальнейших параграфах. Неравенства. Лемма 9.1. Доказательство. (1) X~X1 {доп.} (2) Y~Y1 {доп.} (3) (4) R1 (5) Y~R1Y1 {определение 7.2, 2} (6) Y1 = R1 (Y) {лемма 7.2, 5} (7) (8) (9) (10) (11) Y = Dℓ (R1) {определение 7.1, 5} (12) Z1 = Dℓ (R1) {7, 11} (13) (14) (15) {10, 15} Определим отношения слабого и сильного неравенства. Эти отношения будем обозначать символами, заимствованными из арифметики «обычных» чисел. Определение 9.1
Таким образом, необходимым и достаточным условием того, чтобы мощность множества Х была меньше или равно мощности множества Y, является равночисленность множества Х и некоторого подмножества Y. Заметим, что из леммы 9.1 следует: если Точная формула определения 9.1следующая:
Из определения 9.1и теоремы 7.1аследует: Следствие 9.1.
Заметим еще, что замена под квантором выражения
Определение 9.2.
Легко видеть, что оба определенных отношения являются обобщениями соответствующих отношений арифметики натуральных чисел. Лемма 9.2. Доказательство. (1) (2) X~Y {аксиома 7.1, 1} (3) (4) Определение 9.2 и лемму 9.2можно записать также в следующей форме: m < n ≡ m m = n → m На основании этих формул и теоремы исчисления предложений:
мы устанавливаем истинность. Теорема 9.1. m Следующая теорема называется теоремой Кантора-Бернштейна: Теорема 9.2. m Мы не будем приводить трудного доказательства этой теоремы, а ограничимся лишь указанием, в чем состоит основная мысль этого доказательства. Пусть На основании этих допущений можно показать, что сущесвует взаимнооднозначное отношение T, левая область которого – х, а правая – y. Теорема 9.3. a) m < n → m b) n < m → m c) m = n → ~(m < n) d) m = n → ~(n < m) e) m < n → ~(n Доказательство. Формулы а и b следуют из определения 9.2. Из этих формул с помощью контрапозиции мы получаем формулы с и d. Приводим доказательство формулы е: (1) m < n {доп.} (2) n (3) m (4) m (5) m = n {теорема 9.2, 2, 4} Противоречие. {3, 5} Теорема 9.4. m Мы снова опускаем доказательство этой теоремы и ограничиваемся указанием его основной мысли.
m Из теорем 9.4 и 9.1следует, что для любых двух кардинальных чисел имеет место одно из следующих соотношений: m < n n < m m = n Из теоремы 9.3следует, что может иметь место не более одного из этих отношений. Этот факт мы сформулируем кратко: для кардинальных чисел имеет место принцип трихатолии. Из того, что Теорема 9.5. a) b) Если n – натуральное число, то n < Следующей леммой мы будем пользоваться в дальнейших параграфах: Лемма 9.5. a) m < n →m∙f b) m < n →mk Доказательство. a. (1) m < n {доп.} (2) (3) Z1 (4) (5) (6) m∙f b. В аналогичном доказательстве формулы b используется следствие 8.1(Z
Степенное множество. Определение 10.1. Множество 2Y называется степенным множеством. Таким образом, элементами степенного множества 2Y являются все подмножества множества Y. Лемма 10.1. Доказательство. Пусть М1 – семейство всех одноэлементных множеств {m}, единственный элемент которых m принадлежит М, и только таких множеств. Тогда: {m} Очевидно, что любое из множеств {m} есть подмножество множества М. Отсюда: М1 Обозначим через R1 отношение, сопоставляющее любому элементу m множества М одноэлементное множество {m}. Легко видеть, что это отношение устанавливает равночисленность М и М1. Отсюда из формулы (1) и определения 9.1: ( Пусть R – произвольная функция, сопоставляющая индивидам множества индивидов. Мы определим множество Z(R), зависящее от функции R: Определение 10.2. R Таким образом, элемент х левой области отношения принадлежит множеству Z(R) тогда, и только тогда, когда х не является элементом множества, которое ему сопоставляет функция R. Этим определением мы будем пользоваться в доказательствах дальнейших лемм. Лемма 10.2. R Доказательство. (1) R (2) Z(R) Из формулы (2) следует существование элемента х1 левой области отношения R, которому сопоставляется множество Z(R). Таким образом, формулы (3), (4) имеют место. (3) х1 (4) Z(R) = R (x1) (5) x1
(6) x1 Очевидно, что из формулы (6) следует противоречие. Лемма 10.3. Доказательство. (1) (2) (3) R1 (4) Dℓ(R1) = M {определение 7.1, 2} (5) Dp(R1) = 2M {определение 7.1, 2} (6) Z(R1) (7) Z(R1) (8) Z(R1) (9) Z(R1) (10) Z(R1) Противоречие. {9, 10} Теорема 10.1.
Сформулируем определение, которое потребуется в доказательстве следующей теоремы. Определение 10.3.
φА(m) = 1, если m 0, если m Теорема 10.2. Доказательство. Из определения 8.3 ( (1) {0, 1}M ~ 2M (2) (3)
Теорема 10.3.
Эту теорему можно записать в виде: m < 2m Теорема 10.4. Существует бесконечно много (различных) кардинальных чисел, среди которых нет натуральных чисел. Доказательство. Для доказательства этой теоремы достаточно заметить, что по теореме 10.3 каждый элемент последовательности:
|
||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.191.134 (0.124 с.) |

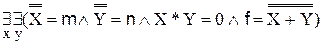

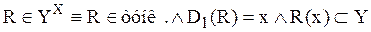
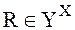 функция R есть отображение множества Х в множество Y.
функция R есть отображение множества Х в множество Y. B~B1 → BA~B1A1 (*)
B~B1 → BA~B1A1 (*)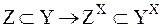
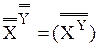
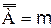 и
и  . По лемме 7.4мы можем считать, что эти множества не пересекаются. Ссылаясь на теорему 7.2b, мы устанавливаем:
. По лемме 7.4мы можем считать, что эти множества не пересекаются. Ссылаясь на теорему 7.2b, мы устанавливаем:

 .
. .
. . Декартову произведению принадлежит X´Y принадлежит любая упорядоченная пара
. Декартову произведению принадлежит X´Y принадлежит любая упорядоченная пара  , где i = 1, 2, …, m; y = 1, 2, …, n. Очевидно, что таких пар
, где i = 1, 2, …, m; y = 1, 2, …, n. Очевидно, что таких пар 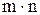 . Таким образом, умножение натуральных чисел – частный случай умножения кардинальных чисел. Далее заметим, что всякое отображение множества Y в множество Х однозначно определит n-численную последовательность
. Таким образом, умножение натуральных чисел – частный случай умножения кардинальных чисел. Далее заметим, что всякое отображение множества Y в множество Х однозначно определит n-численную последовательность ,
,
 {определение 8.1, 1}
{определение 8.1, 1}  {теорема 2.2a}
{теорема 2.2a} {4}
{4} {5,2,3}
{5,2,3}
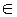 X
X  и
и  это отношение устанавливает равночисленность множеств. Отсюда из определения 8.2и аксиомы 7.1следует равенство:
это отношение устанавливает равночисленность множеств. Отсюда из определения 8.2и аксиомы 7.1следует равенство:

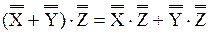
 {определение 8.2, 2}
{определение 8.2, 2}  {теорема 5.1b, 1}
{теорема 5.1b, 1} {определения 8.1, 8.2, 4}
{определения 8.1, 8.2, 4} {теорема 5.1a}
{теорема 5.1a} {6}
{6} {7, 3, 5}
{7, 3, 5}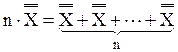
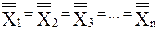
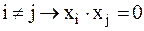


 – это множество всех упорядоченных n-ок <х1,х2,…,хn>, причем х1, х2, …, хn
– это множество всех упорядоченных n-ок <х1,х2,…,хn>, причем х1, х2, …, хn 

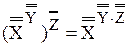

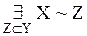 {доп.}
{доп.} {4}
{4}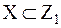 {4}
{4}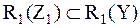 {теорема 6.1, 7}
{теорема 6.1, 7} {9, 6}
{9, 6}  {лемма 7.3, 4, 12}
{лемма 7.3, 4, 12}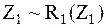 {лемма 7.2, 4, 13}
{лемма 7.2, 4, 13} {теорема 7.1b, c, 1, 8, 14}
{теорема 7.1b, c, 1, 8, 14}
 «≤ » − слабое неравенство
«≤ » − слабое неравенство  ,
, 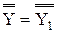 ,
, 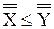 , то и
, то и  .
.
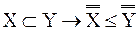 «<» − слабое неравенство
«<» − слабое неравенство выражением
выражением  не позволила бы заменить знак ≤ знаком <, потому что, например, множество всех натуральных чисел, превосходящих некоторое определенное число, есть собственная часть можества всех натуральных чисел, но мощности этиъ множеств равны.
не позволила бы заменить знак ≤ знаком <, потому что, например, множество всех натуральных чисел, превосходящих некоторое определенное число, есть собственная часть можества всех натуральных чисел, но мощности этиъ множеств равны. «<» – сильное неравенство
«<» – сильное неравенство
 {доп.}
{доп.} {теорема 1.4a}
{теорема 1.4a}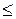 n
n 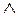 m
m 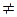 n
n
 m < n
m < n =m и
=m и 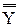 =n. Из условий теоремы следует существование подмножества Z множества X и подмножества U множества Y, а также отношений R и S, таких, что Х~RU и Y~SZ.
=n. Из условий теоремы следует существование подмножества Z множества X и подмножества U множества Y, а также отношений R и S, таких, что Х~RU и Y~SZ.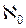 =
=  и f =
и f =  , а также из следствия 9.1 и определения 9.2 следует:
, а также из следствия 9.1 и определения 9.2 следует: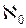 .
. 1 = m
1 = m  1 = n
1 = n  1 = f {теорема 7.2c}
1 = f {теорема 7.2c}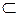 Y1
Y1  1 = m {аксиома 7.1, 3, 2}
1 = m {аксиома 7.1, 3, 2} {теорема 5.1d, 3}
{теорема 5.1d, 3} {следствие 9.1, 5}
{следствие 9.1, 5}

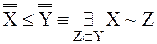 ) следует лемма.
) следует лемма. R(x)].
R(x)].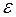 функц. → Z(R)
функц. → Z(R) 
 {доп. к. д.}
{доп. к. д.} {аксиома 7.1, определение 7.2, 1}
{аксиома 7.1, определение 7.2, 1}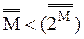
 Пусть М – произвольное множество, и пусть А
Пусть М – произвольное множество, и пусть А 
 {аксиома 7.1, 1}
{аксиома 7.1, 1}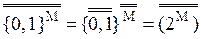 {определение 8.4}
{определение 8.4} {2, 3}
{2, 3} {теорема 10.1, теорема 10.2}
{теорема 10.1, теорема 10.2} ,
,  ,
, 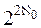 , … менее следующего за ним.
, … менее следующего за ним.


