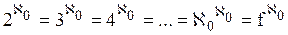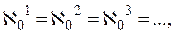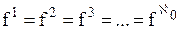Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множества бесконечные в смысле Дедекинда.Содержание книги
Поиск на нашем сайте
Обычно понятие бесконечности понимается так, что бесконечными считаются те, и только те, непустые множества, мощность которых отлична от любого натурального числа. Мы сформулируем определение бесконечного множества, не пользуясь понятием натурального числа (значение того факта, что понятие бесконечного множества может быть определено без ссылки на понятие натурального числа, делают очевидным рассуждения §6 «Приложения»). Это определение принадлежит немецкому математику Р. Дедекинду. Определение 11.1. X есть множество бесконечное в смысле Дедекинда Множество ≡ Таким образом, необходимым и достаточным условием бесконечности в смысле Дедекинда множества является равночисленность данного множества и некоторой его собственной части. Определение 11.2. Мощности бесконечных в смысле Дедекинда множеств называются трансфинитными кардинальными числами. Очевидно, что мощность произвольного бесконечного в смысле Дедекинда множества отлична от нуля и любого натурального числа. Возникает вопрос, вено ли обратное, то есть является ли произвольное множество, мощность которого отлична от нуля и любого натурально числа, бесконечным в смысле Дедекинда. Эта теорема представляется в норме очевидной. Но для ее доказательства необходима новая аксиома (так называемая аксиома выбора), о которой речь будет идти в §14. В доказательства следующей леммы мы воспользуемся четырьмя теоремами алгебры множеств (ср. упражнения b, c, d, e, f §1): I. II. III. IV. Лемма 11.1. Доказательство. (1) (2) Из (2) и теоремы 7.3:( (а) p1, p2, p3, … запас которой – множество P и в которой ни один член не повторяется. Обозначим через P1 запас последовательности (b) p2, p4, p6, … Oчевидно, что (3) Легко видеть, что отношение, сопоставляющее каждому элементу последовательности (а) элемент последовательности (b) с индексом в два раза большим, устанавливает равночисленность множеств P и P1. Таким образом, верна формула (4): (4) P ~ P1 (5) Z = X − P {обозначения} (6) X1 = Z + P {обозначения} (7) X = Z + P {I, 1, 5} (8) P∙Z = 0 {III, 5} (9) P1∙Z = 0 {IV, 3, 8} (10) Z + P ~ Z + P1 {лемма 7.5a, теорема 7.1a, 4, 8, 9} (11) X ~ X1 {10, 6, 7} (12) X1
Лемма 11.2. Доказательство. (1) (2) (3) (4) (5) (6) R1 Заметим, что для каждого х (7) Существование этого элемента гарантирует формула (2). (8) (9) x Последовательность: (а) р1, р2, р3, … мы определяем так: член р1 уже был определен {ср. (7)}. (10) k > 1 → pk = R1 (pk-1) Из формул (7), (9), (10) и (2) несложной индукцией мы получаем (11): (11) рi (12) r > S (2.1) r > S (2.1) pr-1 ≠ ps-1 {доб. доп.} (2.3) R1(pr-1) ≠ R1(ps-1) {лемма 6.3b, 11, 5, 2.2} (2.4) pr ≠ ps {2.1, 2.2, 10} Из (12) и из того, что из формул (2.1) и (2.2) следует формула (2.4), мы получаем индукцией: (13) r > S → pr ≠ ps Таким образом, в последовательности (а) члены не повторяются. Обозначим через Р запас этой последовательности. Тем самым по теореме 7.3мы получим: (14) (15)
Теорема 11.1. Множество Х бесконечно в смысле Дедекинда ≡ {лемма 11.1 ( Таким образом, необходимым и достаточным условием того, чтобы множество было бесконечным в смысле Дедекинда, является наличие в нем счетного подмножества. Из теоремы 11.1, определения 11.2: (Мощности бесконечные в сонном Дедекинда множеств называется трансфинитными кардинальными числами) и следствия 9.1: ( Следствие 11.1. Кардинальное число m трансфинитно ≡ Отсюда и из теоремы 9.5аследует: Следствие 11.2. Кардинальные числа Лемма 11.3. Доказательство. Для доказательства леммы достаточно принять, что Х – множество всех нечетных натуральных чисел, а Y – множество всех четных натуральных чисел. Лемма 11.4. (n – означает здесь произвольное натуральное число). Доказательство. Для доказательства леммы достаточно, принят, что элементы множества Y – числа 1, 2, …, а элементы множества Х – числа n+1, n+2, …. Теорема 11.2. Если Х – бесконечное в смысле Дедекинда множество, (1) Доказательство. Из теоремы 11.1следует существование счетной части Р множества Х. Из лемм 11.3 и 11.4 следует, что: (2) Р ~ P + Y очевидно, имеет место такие соотношения: (3) Х – Р ~ Х – Р Мы можем считать, что: (4) Х∙Y = 0 из формул (2), (3) и (4), а также из леммы 7.5aследует, что: (Х – Р) + Р ~ (X – P) + (P + Y) Отсюда легко следует, что:
Таким образом, формула (1) имеет место. Теорема 11.3. Если ( (1) Доказательство. Из теоремы 11.2и соответствующих допущений следует, что: (2) Очевидно, что:
Отсюда и из следствия 9.1 мы получаем:
Из этой формулы и из формулы (2) следует, что: (3) Ссылаясь еще раз на следствие 9.1, мы получаем:
Отсюда, а также из формулы (3) и теоремы 9.2мы получаем равенство (1). Последние две теоремы можно словесно сформулировать так: (1) Мощность бесконечного в смысле Дедекинда множества не изменяется, если к нему добавляется конечное или счетное множество элементов. (2) Мощность множества не изменяется в результате изъятия из него произвольной конечной или счетной части при условии, что полученное таким путем множество бесконечно в смысле Дедекинда. Очевидно, что тогда и множество, из которого изымается конечная или счетная часть бесконечно в смысле Дедекинда. § 6. Кардинальные числа Вспомним, что кардинальные числа
f = где
Заметим (следствие 11.2) также, что числа Следующая теорема, принадлежащая Кантору, − одна из самых хронологически ранних теорем теории множеств. В доказательства этой теоремы, почти не отличающемся от доказательства Кантора, мы будем пользоваться теоремами теоретической арифметики.
Теорема 12.1. Доказательство. (1) Отсюда и из теоремы 7.3следует существование последовательности: (а) х1, х2, х3, … Члены которой не повторяются, а запас − множество Â, D. Из теорем теоретической арифметики следует, что любое действительное число имеет единственное собственное разложение ∙ в виде бесконечной десятичной дроби. (Несобственным называется разложение, в которое, начиная с некоторого места, входит лишь цифра 9. Собственным разложением называется любое разложение, если неверно, что оно несобственное.) несобственное. Очевидно, что все цифры разложения, начиная с некоторого места, могут совпадать с 0. Причем собственные разложения чисел последовательности (а): х1 = с1, у11 у12 у13 … у1n … х2 = с2, у21 у22 у23 … у2n … . . . хn = сn, уn1 уn2 уn3 … уnn … ... Пример. х1 = 2,125… Символы с1, с2 … − обозначают целые части чисел х1, х2 … Символ уij обозначает j-ю после запятой цифру десятичного разложения числа xi. Определим последовательность:
2, если ynn = 1 Очевидно, что: (2) 0, z1, z2, z3, … есть собственное разложение в бесконечную десятичную дробь некоторого действительного числа. Легко видеть (из (**)), что для любого n n-я цифра разложения (2) не совпадает с n-й цифрой разложения числа хn. Поэтому число (2) отлично от любого числа последовательности (а). Это следствие противоречит полученному ранее следствию, что запас последовательности (а) – множество Â. Таким образом, допущение (1) приводит к противоречию. Из определения 9.2 ( Теорема 12.2. Таким образом, мощность множества всех действительных чисел не изменяется в результате изъятия из него счетной части. Доказательство.
Из теоремы 7.3и (1) и (2) следует существование последовательности: (а) х1, х2, х3, … различных действительных чисел, запас которого − множество Х. Так же как и в доказательстве теоремы 12.1мы выводим существование действительного числа z1, отличного от любого члена последовательности (а). Отсюда: z1 Действительное число z2 мы определим как число, отличное от любого числа последовательности: z1, x1, x2, … Поступая далее таким же образом, мы получаем бесконечную последовательность: z1, z2, z3, … различных действительных чисел, из которых каждое − элемент множества – Х. Таким образом по теореме 7.3и теореме 11.1данное множество бесконечно в смысле Дедекинда. Отсюда из формулы (2) и теоремы 11.3 [ Если (
Таким образом, теорема имеет место. Лемма 12.1. Доказательство. Равночисленность множеств Лемма 12.2. Доказательство.Равночисленность множеств Теорема 12.3. Таким образом, любой непустой интервал действительных чисел есть множество мощности континуума. В следующих формулах буква n обозначает произвольное натуральное число: Теорема 12.4.
b) c) f + n = f {следствие 11.2, теорема 11.2} d)f + e)f + f = f Доказательство. е. (1) a < b < c Ù a, b, cÎÂ (обозначения) (2) (3) {определение 8.1, 2} (4) f = f +1+f a > b → f +f = f Следствие 12.1. а) b) с) Теорема 12.5. Пусть z 1, z 2, z 3… – произвольная последовательность непересекающихся множеств. Если Доказательство. Пусть z1(i), z2(i), z3(i)… – бесконечная последовательность, члены которой не повторяются, а записываются множество Zi. Легко видеть, что члены последовательности z1(1), z1(2), z2(1), z1(3), z2(2), z3(1), z1(4), … не повторяются и что запас этой последовательности – множество Лемма 12.3. Если счетная сумма конечных множеств бесконечна, то она счетна. Доказательство аналогично теорема 12.5. Лемма 12.4 Множество всех конечных последовательностей, члены которых – числа (1) 0, 1, 2, 3, …, n счетно. Доказательство. Пусть Zi (i = 1, 2, 3 …) – множество всех i-элементных последовательностей, члены которых – числа (1). Очевидно, что для любого i множество Zi конечно, а сумма всех таких множеств бесконечно. Отсюда и из леммы 12.3следует лемма. Теорема 12.6. Доказательство. Обозначим через Р множество всех упорядоченных пар <m,n>, элементы которых – натуральные числа, через Рi (i = 2, 3,...) – множество таких же пар, и удовлетворяющих, кроме того, условию m + n = i. Очевидно, что (1) С другой стороны, из определения множества Р и из определения 8.2следует, что Теорема 12.7. Если n -натуральное число, n ≥ 2, то Доказательство приведем для случая, когда n=10. Общее доказательство существенно не отличается от доказательства этого частного случая. Доказательство.Обозначим через h1 – множество неотрицательных целых чисел ≤ 9, а потому (1) Из определения 8.3следует, что отображение множества h в множество h1 однозначно определяет бесконечную последовательность, члены которой – числа 0, 1, …, 9. Обозначим через С множество всех таких последовательностей. Из формулы (1) поэтому следует: (2) Обозначим далее через С1 множество всех принадлежащих С последовательностей, любой член которых, начиная с некоторого, равен 9. Из леммы 12.4следует, что: (3) Очевидно, имеет место также соотношение: (4) Из теории чисел, следует, что любой последовательности, принадлежащей С − С1, соответствует точно одно число полуинтервала Это число есть так называемая бесконечная десятичная дробь, целая часть которой – число 0, а следующими друг за другом после запятой цифрами являются следующие друг за другом члены последовательности, с которой приведена в соответствие данная дробь. В этой дроби, начиная с некоторого места, не могут встретиться только девятки (однако могут встретиться только нули). В общем доказательстве теоремы здесь следовало бы сослаться на аналогичную теорему теории чисел о разложении действительного числа в бесконечную дробь в любой системе счисления с основанием, большим или равным 2. Это единственный пункт, в котором приведенное доказательство теоремы 12.7(при n=10), отличается от общего доказательства. Отсюда и из следствия 12.1мы получаем: (5) Из формул (2) – (5) и теоремы 12.4следует также равенства: Таким образом, доказательство теоремы для случая, когда n=10, закончено. Частным случаем теоремы 12.7является: Теорема 12.8. Заметим, что из этой теоремы и теоремы 10.1: Доказательство данной теоремы, которое мы провели интересно, однако в том отношении, что в нем применяется так называемый диагональный метод, с помощью которого было доказано много важных математических теорем. В следующих формулах n обозначает произвольное натуральное число: Теорема 12.9. a) b) c) d) e) f) g) h) Доказательство. а) b) c) d) e) f) g) (1) n < (2) n × f ≤ (3) f ≤ f × В аналогичном доказательстве формулы h мы пользуемся леммой 9.3b. Из теоремы 12.9d: Таким образом, существует взаимнооднозначное отображение множества точек плоскости на множество точек прямой. Канторовское доказательство теоремы 12.9d, которая казалась парадоксальной ввиду этих следствий, склонило математиков к исследованию отображений плоскости на прямую. Уже через несколько лет после доказательства теоремы 12.9d было показано, что не существует взаимооднозначного и одновременно непрерывного отображения множества точек плоскости на множество точек прямой. Из теоремы 12.9h следует: Следствие 12.1. Множество всех бесконечных последовательностей, члены которых – натуральные числа, имеет мощность континуума. Сходным образом из теоремы 12.9f следует: Следствие 12.2. Множество всех бесконечных последовательностей, члены которых – действительные числа, имеет мощность континуума. Заметим, что из теорем 12.4а, b следуют равенства:
А из теорем 12.4с, d, e следуют равенства: f +1= f +2 = f + 3= … = f + Таким образом, суммы координатных чисел могут быть равны, когда равны их первые слагаемые, но неравны вторые. Поэтому обратная к сложению кардинальных чисел операция неоднозначна. Вследствие этого мы не вводим в арифметику кардинальных чисел вычитания. Из теорем 12.9а и 12.6следуют равенства: 1 × Из теорем 12.9с, d, g следуют равенства: 1 × f = 2 × f = 3 × f = … = f × Поэтому обратная к умножению кардинальных чисел операция также неоднозначна. Заметим еще, что из теорем 12.7 и 12.9f, hследует:
Таким образом, мы видим, что обратная операция к возведению в степень (извлечение корня) кардинальных чисел неоднозначна. Заметим, наконец, что из теоремы 12.9bследуют равенства:
а из теорем 12.9e, f следуют равенства:
Поэтому и другая обратная к возведению в степенно операции (логарифмирование) неоднозначна. Теорема 12.10. Множество всех конечных последовательностей целых чисел счетно. Доказательство. Обозначим через Zi,j (i = 1, 2, 3, …; j = 0, 1, 2, …) множество всех i-элементных последовательностей, в которых наибольший по абсолютной величине член равен j. Очевидно, что для произвольных i и j множество Zi,j счетно. Отсюда и из теоремы 12.5следует теорема: Теорема 12.11. Множество всех неотрицательных чисел, множество всех целых и множество всех рациональных чисел счетны. Множество всех комплексных чисел имеет мощность континуума. Доказательство. Приведем в соответствие каждому натуральному числу равное ему по абсолютной величине отрицательное число. Очевидно, что данное соответствие устанавливает равночисленность множества всех натуральных чисел. Поэтому множество всех отрицательных целых чисел счетно. Очевидно, что множество всех целых чисел есть сумма всех натуральных чисел, множества всех отрицательных целых чисел и множества, единственный элемент которого – число 0. Отсюда и из теорем 12.4а, b следует, что множество всех целых чисел счетно. Заметим, что из определения 8.2, теоремы 12.6 и из того, что множество всех целых чисел счетно, следует также счетность множества всех упорядоченных пар, первые элементы которых – целые, а вторые элементы – натуральные числа. Любое рациональное число можно записать в виде несократимой дроби, в которой числитель – целое, а второй − натуральное число, причем данные числа взаимно простые. Множество всех таких пар есть подмножество множества всех упорядоченных пар, в которых первый элемент – целое, а второй − натуральное число, а потому оно и есть подмножество счетного множества. Таким образом, мощность всех рациональных чисел меньше или равна С другой стороны, число Отсюда и из теоремы 9.2следует, что множество всех рациональных чисел счетно. Наличие у множества всех комплексных чисел мощности континуума следует непосредственно из того, что комплексные числа – это упорядоченные пары действительных чисел, и из определения 8.2 и теоремы 12.9d.
|
||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.93.242 (0.009 с.) |

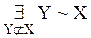
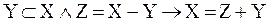
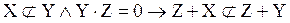
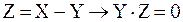
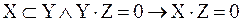
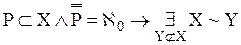
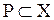 {доп.}
{доп.}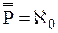 {доп.}
{доп.}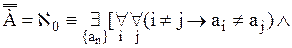 множество А есть запас последовательности {an}) следует существование бесконечной последовательности
множество А есть запас последовательности {an}) следует существование бесконечной последовательности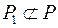
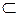 X {II, 3, 8, 6, 7}
X {II, 3, 8, 6, 7}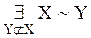 {11, 12}
{11, 12}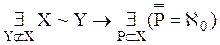
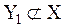 {1}
{1}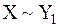 {1}
{1}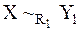 {определение 7.2 (
{определение 7.2 (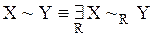 ), 3}
), 3}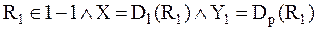 {определение 7.1, 4}
{определение 7.1, 4}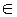 функц. {определение 6.6 (R
функц. {определение 6.6 (R 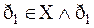
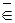
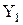
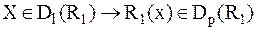 {следствие 6.3с, 6}
{следствие 6.3с, 6}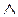 S = 1 → pr ≠ ps {7, 9, 10, 11}
S = 1 → pr ≠ ps {7, 9, 10, 11} 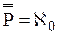
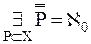 {14, 15}
{14, 15}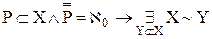 ), лемма 11.2 (
), лемма 11.2 (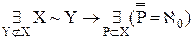 ), определение 11.1 (X есть бесконечное в смысле Дедекинда множество ≡
), определение 11.1 (X есть бесконечное в смысле Дедекинда множество ≡ 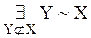 )}
)}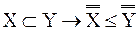 ) следует:
) следует: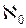 ≤ m
≤ m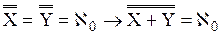
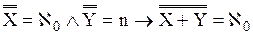
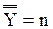 (n – произвольное натуральное число) или
(n – произвольное натуральное число) или 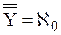 , то
, то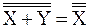
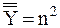 или
или 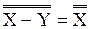 (n
(n 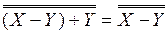
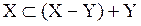
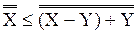
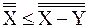
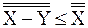
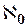 и f.
и f.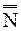
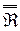
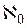 ≠ f
≠ f Zn= 1, если ynn ≠ 1 (**)
Zn= 1, если ynn ≠ 1 (**)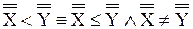 ), теоремы 9.5а (
), теоремы 9.5а (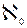
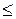 f) и теоремы 12.1 (
f) и теоремы 12.1 (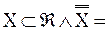
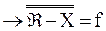 .
.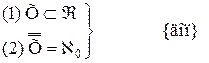
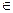 D – Х или z1
D – Х или z1 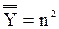 или
или 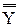 =
= 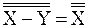 (n
(n 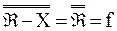 .
.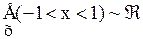
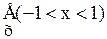 и Â определяется отношением:
и Â определяется отношением: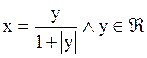
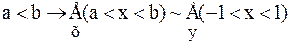
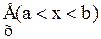 и
и 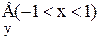 устанавливается отношением:
устанавливается отношением: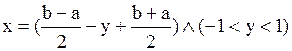
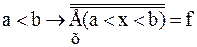 {лемма 12.1, лемма 12.2}
{лемма 12.1, лемма 12.2}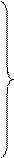 a)
a)  {1}
{1}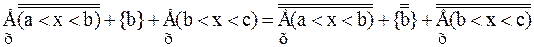
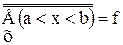
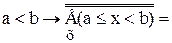 f
f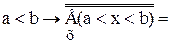 f
f 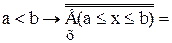 f
f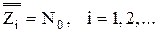 , то
, то 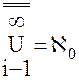 .
. . Отсюда и из теоремы 7.3 следует теорема.
. Отсюда и из теоремы 7.3 следует теорема.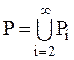 и множество Р бесконечно. Легко видеть, что множества Р2, Р3, … конечны. Отсюда и из леммы 12.3следует, что
и множество Р бесконечно. Легко видеть, что множества Р2, Р3, … конечны. Отсюда и из леммы 12.3следует, что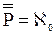
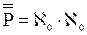
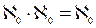 {1, 2}
{1, 2}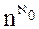 = f.
= f.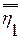 = 10. Отсюда и из определения 8.4получаем:
= 10. Отсюда и из определения 8.4получаем: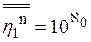
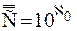
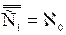
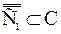
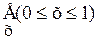 .
.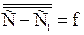
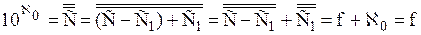
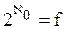
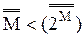 непосредственно следует теорема 12.1: À0 ≠ f.
непосредственно следует теорема 12.1: À0 ≠ f.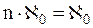
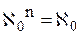
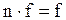
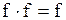
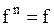
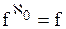
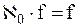
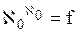
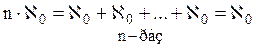 {теоремы 8.3, 12.4b}
{теоремы 8.3, 12.4b}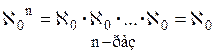 {теоремы 8.4, 12.6}
{теоремы 8.4, 12.6}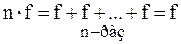 {теоремы 8.3, 12.4e}
{теоремы 8.3, 12.4e}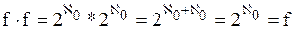 {теоремы 12.8, 12.4b, 8.5}
{теоремы 12.8, 12.4b, 8.5}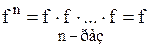 {теоремы 12.9d, 8.4}
{теоремы 12.9d, 8.4}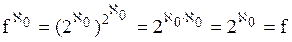 {теоремы 12.8, 12.4b, 8.5}
{теоремы 12.8, 12.4b, 8.5}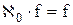 {теоремы 9.2, 3}
{теоремы 9.2, 3}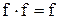 следует, что множество упорядоченных пар действительных чисел равночисленно множеству действительных чисел. Как известно, множество точек прямой равночисленно множеству действительных чисел, а множество точек плоскости равночисленно множеству упорядоченных пар действительных чисел (координат этих точек). В результате получаем следствие, по которому множество точек плоскости равночисленно множеству точек прямой.
следует, что множество упорядоченных пар действительных чисел равночисленно множеству действительных чисел. Как известно, множество точек прямой равночисленно множеству действительных чисел, а множество точек плоскости равночисленно множеству упорядоченных пар действительных чисел (координат этих точек). В результате получаем следствие, по которому множество точек плоскости равночисленно множеству точек прямой.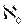 = f × f
= f × f