
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип Гюйгенса - Френеля. Метод зон Френеля.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Под дифракцией света обычно понимают все явления, приводящие к отклонению от законов геометрической оптики. Если фронт волны распространяется в пустоте или однородной неограниченной среде, то луч всегда прямая линия. Если же часть волнового фронта ограничить какими-либо препятствиями, то на границе этих препятствий свет уже не распространяется прямолинейно, а отклоняется на угол порядка λ/d, где λ - длина волны, a d - размер препятствия (или отверстия в препятствии). Дифракция наблюдается также при наличии в среде прозрачных неоднородностей, т.е. включений с другим показателем преломления. В результате дифракции на экране граница света и тени от препятствия оказывается размытой. Более того, вблизи границы и в области тени, и в области света наблюдаются интерференционные полосы. Качествен Рассмотрим метод зон Френеля на примере дифракции на круглом отверстии. Пусть имеется точечный источник света S и экран МN с круглым отверстием (Рис.2). Требуется определить освещенность в точке А, лежащей на прямой OS, перпендикулярной MN. Отверстие пропустит лишь часть фронта сферической волны, действием которой будет определяться освещенность в точке А. Колебания от точки 0 приходят в точку А раньше, чем от других точек фронта волны, например, от точки 1 или 1'. Т.е. колебания от точек 0 и 1 (1') имеют в точке А различные фазы. Разность фаз зависит от разности расстояний (разности хода) между точкой А и соответствующими точками фронта волны. При разности хода D=l/2 (l - длина волны) колебания приходят в противофазе и гасят друг друга.
Этот факт использовал Френель, предложив разбить открытую часть фронта волны на области (зоны) так, чтобы разность фаз вторичных волн от одной зоны не превышала p. Сложение таких волн от одной зоны приводит к их взаимному усилению. Поэтому каждую зону можно рассматривать как источник вторичных волн, имеющих определенную фазу. Таким образом, в случае сферического фронта волны центральная зона I представляет собой сферический сегмент, ограниченный точками, для которых r1 = r0+λ/2. Соседняя зона II представляет собой кольцевую область на сфере, заключенную между точками, для которых с одной стороны r =r1, с другой стороны r2= r1 + λ/2 = r0 + λ. Последующие зоны будут также иметь форму сферических колец, ограниченных снаружи точками, для которых r= r0 + k λ/2, где k - номер зоны. Используя формулу для площади поверхности сферического сегмента, можно показать, что площади всех зон Френеля приблизительно равны. Так как расстояния от зон Френеля до точки А и углы, под которыми они видны из точки А, мало различаются по величине, то можно считать, что амплитуды колебаний в точке А, приходящих от различных зон Френеля, практически равны. Поскольку колебания от соответствующих точек соседних зон приходят в противофазе, то колебания от любых двух соседних зон взаимно уничтожаются. Если отверстие пропускает такую часть фронта волны, что на ней помещаются две зоны Френеля или любое четное число зон Френеля, в точке А будет наблюдаться темнота. Если в отверстии укладывается нечетное число зон Френеля, в точке А будет свет.
Обозначим расстояние от источника до отверстия через a, от отверстия до точки А – через b. Построим сферический фронт волны радиусом SN = R0 = a+h, где h – высота сферического сегмента, вырезанного на сферической поверхности плоскостью MN. Из треугольника SNO имеем:
Поскольку h мало по сравнению с a, то
Если в отверстии уложилось целое число K зон Френеля, тогда из условия построения зон:
Из рисунка видно, что
Подставляя вместо r 0 и r 02 (3) и (4) в (2) и пренебрегая членами второго порядка малости
Из треугольника AON имеем:
откуда:
Следовательно, число зон, уложившихся в отверстии MN, зависит не только от радиуса отверстия, но и от расстояний от отверстия до источника и точки наблюдения, а также от длины волны. Если, не изменяя расстояния от источника до отверстия и радиус отверстия, перемещаться вдоль оси SQ, т.е. изменять b, то К - число открытых зон будет монотонно изменяться, принимая попеременно, то четные, то нечетные значения, т.е. на оси SQ в различных местах мы будем наблюдать в центре дифракционной картины то темноту, то свет. Если наблюдения произвести из точки, для которой b по формуле (6) дает нецелочисленное значение К, то картина в центре будет менее контрастной. Мы рассмотрели картину дифракции в точках на оси SQ. Теоретическое рассмотрение картины дифракции в соседних с осью точках связано с дополнительными трудностями. Однако, очевидно, что дифракционная картина должна быть симметричной относительно точки, лежащей на оси, так как в точках, находящихся на одном и том же расстоянии от центральной точки, условия дифракции будут одинаковы. Итак, если в точке на оси мы наблюдаем светлое пятно, то вокруг него мы обнаружим темное кольцо, вокруг которого заметим светлое кольцо, т.е. картина дифракции на круглом отверстии представляет собой чередующиеся темные и светлые кольца. Число колец зависит от числа открытых зон и, следовательно, от места наблюдения. На рис.4 представлено несколько изображений картин дифракции на круглом отверстии по мере приближения к отверстию (т.е. по мере уменьшения расстояния b).
Рис.4. Дифракционная картина Френеля на круглом отверстии на разных расстояниях b от отверстия до экрана. Число открытых зон увеличивается слева направо от 2 до 6. Размер картины уменьшается, приближаясь к диаметру отверстия.
Если на пути света от точечного источника S установить малых размеров диск D, то на экране Р также будет наблюдаться
дифракционная картина. Рассмотрим, чему равна амплитуда колебаний в точке А, лежащей на оси SO. Используя метод зон Френеля (Рис.5), получим, что амплитуда колебаний в точке А будет равна половине амплитуды, обусловленной первой открытой зоной. Если размер диска невелик, то действие первой открытой зоны практически не отличается от действия центральной зоны свободной волны и освещенность в точке А, как и в других точках линии SOА, достаточно удаленных от диска, будет такой же, как и при отсутствии диска. Таким образом, в центре области геометрической тени будет наблюдаться светлое пятно(пятно Пуассона). За пределами геометрической тени наблюдается картина в виде чередования темных и светлых колец (Рис.6).
Причем по мере удаления от центра кольца становятся все менее и менее резкими. Число колец, как всегда при интерференции, близко к величине На рис. 7 приведены фотографии дифракционной картины Френеля на вертикальной щели. Начальная ширина щели соответствует примерно одной открытой зоне Френеля, конечная ширина – семи открытым зонам Френеля. Вертикальный размер картины определяется размерами светового пучка, падающего на щель. Когда в щели укладывается нечетное число зон Френеля, в центре картины наблюдается светлая полоса, в случае четного числа зон – темная полоса.
Зонная пластинка Френеля
Дифракция Фраунгофера Если расстояние α (Рис.3) увеличивать до бесконечности, то лучи от источника S можно будет считать параллельными, а волновой фронт плоским. Параллельный пучок можно также получить с помощью линзы (Рис. 9, линза 1). Можно также искусственно удалить и точку наблюдения в бесконечность, поставив линзу 2, а экран - в её задней фокальной плоскости. Такая постановка наблюдения дифракции была предложена Фраунгофером. Картину дифракции при такой постановке легче рассчитывать. Рассмотрим особенности дифракционной картины Фраунгофера на примере дифракции света на щели (Рис.9). Для равномерного освещения длинной щели удобно взять источник также в виде узкой протяженной светящейся щели, параллельной щели Щ. Лучи загибают за края щели под разными углами. Угол α называется углом дифракции (Рис.10). Лучи, идущие от разных участков щели под одним и тем же углом α, линза Л2 соберет на экране, расположенном в ее задней фокальной плоскости, в одном месте. Из соображений симметрии ясно, что дифракционная картина будет иметь вид чередующихся светлых и темных полос, параллельных краям щели. Каждому углу α соответствует определенная полоса.
Задача заключается в том, чтобы выяснить, при каких углах α дифракционная полоса будет темной, а при каких – светлой, т.е. найти распределение световой энергии в дифракционной картине. Эту задачу можно решить, используя метод графического сложения амплитуд. Мысленно разобьем открытую часть фронта волны, проходящего через щель, на очень узкие полоски равной ширины, параллельные краям щели (Рис. 10).
на экран в одной и той же фазе, следовательно, вектора – амплитуды выстроятся в прямую линию (Рис.11а), и в центре дифракционной картины будет наблюдаться максимальная освещенность. Пусть
Этой разности хода соответствует разность фаз
Рассмотрим случаи, когда разность хода для крайних лучей будет принимать различные значения. Если Первый минимум появится когда
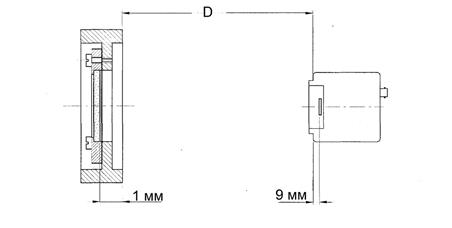
Теоретически распределение интенсивности света в дифракционной картине Фраунгофера на щели в зависимости от угла дифракции α описывается формулой
где I0 – интенсивность света в середине дифракционной картины (в направлении α=0); Iα – интенсивность света в точке, положение которой определяется данным значением угла α. При значении угла дифракции, удовлетворяющем условию
где На рис. 12 представлено изображение дифракционной картины Фраунгофера на вертикальной щели по мере расширения щели. Как видно из рисунка, нулевой максимум наиболее яркий и вдвое шире побочных максимумов. По мере расширения щели дифракционные полосы становятся уже. Размер области дифракционного изображения обратно пропорционален ширине щели. При ширине щели а= λ (
Рис. 12. Дифракция Фраунгофера на вертикальной щели по мере ее расширения слева направо.
Результат дифракции монохроматического излучения на каком-либо препятствии зависит от числа m, перекрываемых им зон. При m >>1 (сотни - тысячи) дифракционные эффекты незначительны и распределение интенсивности приближенно описывается законами геометрической оптики (Рис. 14, плоскость 1). Промежуточное условие (открыты единицы - десятки зон) соответствует дифракции Френеля и приводит к сложному распределению интенсивности, когда в центре картины может наблюдаться и минимум, и максимум (Рис.14, плоскости 2,3 и 4). При m <1 перекрывается малая часть первой зоны и возникает дифракция Фраунгофера или дифракции в дальней зоне (плоскости 6 и 7). Условной границей между двумя видами дифракции считают дистанцию Рэлея R: на этом расстоянии для центральной точки круглое отверстие диаметра D, освещенное плоской монохроматической волной, открывает одну первую зону. Дифракционные распределения в области Фраунгофера имеют идентичный характер, линейно увеличиваясь по мере удаления от экрана с отверстием. Угловой размер центрального дифракционного максимума в дальней зоне определяется отношением длины световой волны к диаметру отверстия. Легко видеть, что на дистанции Рэлея этот угловой сектор имеет линейный размер равный диаметру отверстия D. На рис.14 представлен снимок дифракционной картины на кольце, число открытых зон уменьшается слева направо. На этом примере дифракции на кольце можно проследить плавный переход от геометрического изображения (кадры 1-3) через дифракцию Френеля (кадры 4-7) к дифракции Фраунгофера (кадры 9-11). Условной границе (дистанции Рэлея) между дифракцией Френеля и Фраунгофера соответствует снимок 8 (в кольце укладывается одна зона Френеля).
Рис. 14.Дифракционная картина на кольце. Задания и указания к выполнению В настоящей работе (по выбору преподавателя) студент выполняет три задания. Задание 6 дается наиболее успешным студентам, выполнение задания 6 равноценно выполнению обязательных трех заданий.
Рис.15 Лазер дает практически параллельный пучок лучей, что соответствует плоскому фронту волны. Рассеивающая сферическая линза превращает плоскую волну в сферическую с вершиной в заднем фокусе линзы, который играет роль точечного источника света, находящегося на расстоянии a от отверстия. Радиус отверстия измерьте на компараторе. Задание 2. По дифракционной картине Фраунгофера на щели определите ширину щели a.
Для измерения ширины щели используйте условие дифракционного минимума, которое при a<<r (r - расстояние от щели до экрана) может быть представлено в виде:
где a - ширина щели, xк - расстояние от центрального максимума до минимума К-ого порядка, f - фокусное расстояние линзы, в фокальной плоскости которой располагается экран. Для измерений используйте раздвижную щель с микрометрическим винтом, фокусное расстояние собирающей линзы измерьте на коллиматоре. Для большей точности измерений желательно использовать длиннофокусную линзу и xк определять из измерений расстояния между симметричными минимумами К-ого порядка слева и справа. Оцените погрешность измерений. Задание 4. Рассчитайте и экспериментально измерьте фокусное расстояние амплитудной зонной пластинки Френеля. Для этого: · С помощью компаратора измерьте на пластинке диаметры К зон Френеля (К=1,2,3,4,5,6,7,8). Результаты измерений занесите в таблицу. По формуле (8) рассчитайте фокусное расстояние для разных значений К, найдите среднее значение фокусного расстояния. · Используя зонную пластинку в качестве собирающей линзы, получите уменьшенное и увеличенное изображение нити накаливания лампы проекционного фонаря. Между лампой и зонной пластинкой не забудьте поставить тепловой фильтр. Из результатов измерений отрезков a и b, где a – расстояние между зонной пластинкой и нитью накаливания лампы, b – расстояние между зонной пластинкой и экраном, на котором получается изображение нити накаливания, по формуле отрезков (7) рассчитайте фокусное расстояние зонной пластинки. Оцените точность измерений. Сравните результаты определения фокусного расстояния зонной пластинки Френеля первым и вторым способом. Задание 5. На примере дифракционной картины на круглом отверстии (d=0.8мм) продемонстрируйте плавный переход от дифракционной картины Фраунгофера к геометрическому изображению отверстия, затем к дифракционной картине Френеля. Для постановки этого эксперимента воспользуйтесь оптической схемой, представленной на рис. 17, где Л1-рассеивающая линза с фокусным расстоянием f1~1см, Л2 – собирающая линза (f2~ 9,4 см), Л3 – собирающая линза (f3=11cм), Л4 - собирающая линза (f4=3cм). Линзы Л1 и Л2 используются для уширения пучка параллельных лучей, излучаемых лазером. Установите линзу Л3 от круглого отверстия О на расстоянии 2f3. Тогда
за линзой Л3 в ее задней фокальной плоскости будет находиться дифракционная картина Фраунгофера, при удалении от задней фокальной плоскости линзы Л3 наблюдается переход от дифракционной картины Фраунгофера к дифракционной картине Френеля, которая на расстоянии 2f3 переходит в геометрическое изображение отверстия. На расстояниях >2f3 будут располагаться изображения дифракционных картин Френеля, образующихся за отверстием, причем при удалении от отверстия число зон Френеля, укладывающихся в отверстии, будет уменьшаться, принимая попеременно, то четные, то нечетные значения. В качестве критерия перехода от дифракционной картины Френеля к дифракционной картине Фраунгофера используется условие, при котором в отверстии укладывается одна зона Френеля. Расстояние b, соответствующее этому условию, называется дистанцией Рэлея. Сначала перемещая линзу Л4, сфокусируйте ее на заднюю фокальную плоскость линзы Л3 и получите на экране изображение дифракционной картины Фраунгофера. Продолжая перемещать линзу Л4 вправо, наблюдайте переход от дифракционной картины Фраунгофера к дифракционной картине Френеля и к геометрическому изображению отверстия, затем переход от геометрического изображения отверстия к дифракционной картине Френеля. Объясните наблюдаемые изменения в дифракционных картинах Френеля. Рассчитайте для данного отверстия дистанцию Рэлея. По каким признакам можно отличить дифракционную картину Фраунгофера от дифракционной картины Френеля? Задание 6.
Рис. 18 Используя автоматизированное установкуАРМС-7, исследовать распределение интенсивности света в дифракционной картине сначала на одной, затем на двух щелях. На рис. 18 представлен внешний вид рабочего места АРМС 17. АРМС 7 представляет собой компьютерную систему на основе управляемой твердотельной ПЗС камеры. В состав системы входят видеокамера, блок управления видеокамерой, персональный компьютер с установленной в нем платой ввода изображения типа Flay Video, оптическая скамья стержневого типа L=200 mm, полупроводниковый лазер (λ=650 нм), дифракционный объект МОЛ-01. В комплект программного обеспечения входит программа обработки видеоизображения OSC16. Формирование дифракционных изображений от структур тест-объекта МОЛ-01 производится непосредственно на приемной площадке ПЗС-камеры. Система может работать в режиме визуального наблюдения и в режиме измерений. В режиме визуального наблюдения в камере включены системы автоматического регулирования, данный режим используется как подготовительный перед проведением измерений. В этом режиме удобно навести камеру на объект, и наблюдать за оптическим процессом или объектом. Порядок действий
· Выбрать и зафиксировать на изображении опорную точку (главный максимум) нажатием кнопки «Установка опорной точки». · Сохранить координаты графика с помощью кнопки «Запись строки в файл», файл имеет расширение dat, состоящее из двух столбцов чисел. В этом файле сохраняется зависимость в виде матрицы интенсивности света от номера пикселя. · Открыть Origin двойным нажатием на иконку, находящуюся на рабочем столе.
Рис.19.Определение расстояния между матрицей камеры и поверхностью объекта. где a – ширина щели, L= 11мм + D + 9мм + d*n - расстояние между матрицей камеры и поверхностью объекта (Рис.19), D- расстояние между торцевыми поверхностями оправ, в которых закреплены объект и видеокамера (измеряется линейкой), d-толщина покровного стекла ПЗС-матрицы, n-показатель преломления стекла (d = 1мм, n= 1,5).. · Сравнить значения максимумов интенсивности, полученные из экспериментального графика, с соответствующими теоретическими значениями (14)
Таблица 1. Основные параметры двойных щелей (ряд А)
Для получения зачета необходимо: 1. Уметь получать дифракционную картину от круглого отверстия и узкой щели. 2. Представить отчёт по выполненной работе. 3. Уметь отвечать на вопросы: · Дифракция Френеля. Метод зон Френеля. · От чего зависит количество зон Френеля, укладывающихся в отверстии? · Зонная пластинка Френеля, ее фокусное расстояние. · Какая картина будет наблюдаться, если открыто меньше одной зоны Френеля? · Какая картина будет наблюдаться, если в отверстии укладывается много (>>1) зон Френеля? · Дифракция Фраунгофера. · Распределение интенсивности света в дифракционной картине Фраунгофера от одной щели. · Что будет происходить с дифракционной картиной Фраунгофера при увеличении ширины щели? · Как по дифракционной картине Фраунгофера от щели можно определить длину волны света? · Тест 1 В настоящей работе для проведения косвенных измерений, используя данные полученных дифракционных картин, предлагаются следующие формулы: (1) (8) С постановкой какого эксперимента связаны эти формулы? Выберите правильный ответ:
Тест 2 В настоящей работе для проведения косвенных измерений, используя данные полученных дифракционных картин, предлагаются следующие формулы:
Какие величины в приведенных выше формулах обозначены буквами (1) b, (2) k, (3) xk, (4) f, (5) a, (6) r, (7) a, (8) DX0, (9) L, (10) r? Выберите правильный ответ: 1. Радиус отверстия в формуле (2). 2. Радиус к-ой зоны Френеля в формуле (3). 3. Ширину щели в формулах (4), (5), (6), (7), (8). 4. Угол дифракции. 5. Порядок дифракционного минимума в формулах (4), (6), (7). 6. Порядок дифракционного максимума в формулах (4), (6), (7). 7. Расстояние от отверстия до экрана. 8. Расстояние от зонной пластинки до экрана в формуле (1). 9. В формуле (1) расстояние от зонной пластинки до нити накаливания проекционной лампы. 10. В формуле (2) расстояние от точечного источника света до отверстия. 11. В формуле (1) фокусное расстояние зонной пластинки. 12. В формуле (6) фокусное расстояние линзы. 13. Фокусное расстояние зонной пластинки формуле (6). 14. Фокусное расстояние линзы в формуле (1). 15. Координату к-ого дифракционного минимума. 16. Координату к-ого дифракционного максимума. 17. Расстояние между матрицей камеры и поверхностью объекта. 18. Расстояние от щели до экрана. 19. Ширину центрального дифракционного максимума в дифракционной картине от щели. 20. Число зон Френеля в формуле (2) и (3). 21. Расстояние от нити накаливания проекционной лампы до зонной пластинки в формуле (1). 22. Радиус отверстия в формуле (3). 23. Правильного ответа нет. Тест 3 (1). Какими свойствами обладают зоны Френеля? (2). При каком условии в центре дифракционной картины Френеля от круглого отверстия будет наблюдаться темное пятно? (3). При каком условии в центре дифракционной картины Френеля от круглого отверстия будет наблюдаться светлое пятно? (4). По каким признакам можно отличить дифракционную картину Фраунгофера от дифракционной картины Френеля? (5). Как изменится число зон Френеля, укладывающихся в отверстии при увеличении расстояния от отверстия до места наблюдения дифракционной картины? (6). Как изменится дифракционная картина Фраунгофера от щели при увеличении ширины щели? (7). При каком условии в дифракционной картине Фраунгофера от щели будут наблюдаться темные полосы? (8). При каком условии в дифракционной картине Фраунгофера от щели будут наблюдаться светлые полосы? Выберите правильный ответ: 1. При увеличении ширины щели дифракционная картина сожмется. 2. При увеличении ширины щели дифракционна
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 557; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.140.108 (0.012 с.) |

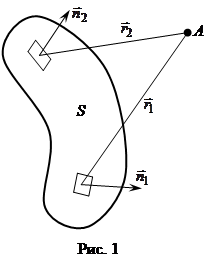 но дифракцию света можно объяснить, исходя из принципа Гюйгенса. Амплитуды колебаний, пришедших в точку А от различных участков волновой поверхности S (Рис. 1), зависят от расстояний ri этих участков до точки А, их площади и угла между нормалью ni к участку и направлением на точку А. При нахождении результирующей амплитуды колебаний от всех участков необходимо учитывать ещё и то, что фазы отдельных колебаний могут не совпадать из - за различия расстояний ri до точки А. Таким образом, нахождение результирующей амплитуды колебания, а, следовательно, и освещенности в какой-либо точке дифракционной картины в общем случае довольно сложная задача, связанная с интегрированием. В ряде случаев для исследования дифракционных картин может быть применен более простой метод, так называемый метод зон Френеля.
но дифракцию света можно объяснить, исходя из принципа Гюйгенса. Амплитуды колебаний, пришедших в точку А от различных участков волновой поверхности S (Рис. 1), зависят от расстояний ri этих участков до точки А, их площади и угла между нормалью ni к участку и направлением на точку А. При нахождении результирующей амплитуды колебаний от всех участков необходимо учитывать ещё и то, что фазы отдельных колебаний могут не совпадать из - за различия расстояний ri до точки А. Таким образом, нахождение результирующей амплитуды колебания, а, следовательно, и освещенности в какой-либо точке дифракционной картины в общем случае довольно сложная задача, связанная с интегрированием. В ряде случаев для исследования дифракционных картин может быть применен более простой метод, так называемый метод зон Френеля.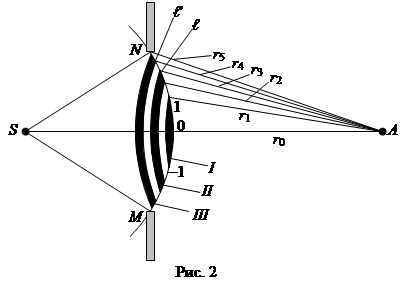
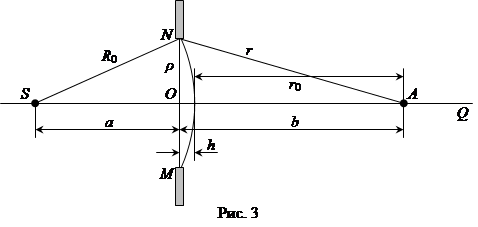 Следовательно, если мы хотим узнать будет ли в точке А свет или темнота, мы должны определить какое число зон Френеля укладывается в отверстии. Пусть S – точечный источник света, SQ – оптическая ось, MN – отверстие в непрозрачном экране, A – точка наблюдения, ρ – радиус отверстия (Рис.3).
Следовательно, если мы хотим узнать будет ли в точке А свет или темнота, мы должны определить какое число зон Френеля укладывается в отверстии. Пусть S – точечный источник света, SQ – оптическая ось, MN – отверстие в непрозрачном экране, A – точка наблюдения, ρ – радиус отверстия (Рис.3).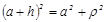
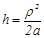 (1)
(1)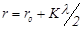
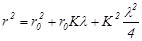 (2)
(2)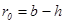 (3) и
(3) и 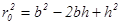 (4)
(4)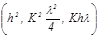 , приближенно имеем:
, приближенно имеем: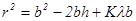 (5)
(5)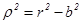 , или, используя (5) и подставляя вместо h его выражение из (1), получим:
, или, используя (5) и подставляя вместо h его выражение из (1), получим: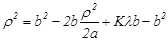 ,
,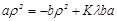 . Решая последнее уравнение относительно К, получим:
. Решая последнее уравнение относительно К, получим: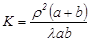 (6)
(6)
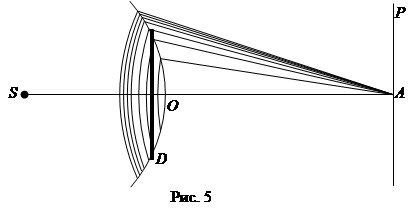

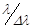 , где Δλ - полоса пропускания применяемого светофильтра.
, где Δλ - полоса пропускания применяемого светофильтра.
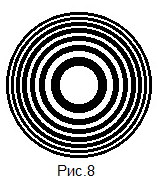 Если на пути световой волны, исходящей от точечного источника S, поставить диафрагму, которая перекроет все четные или все нечетные зоны Френеля (Рис.8), то интенсивность света в точке А резко увеличится. Такая диафрагма действует подобно собирающей линзе и называется амплитудной зонной пластинкой Френеля. Представляя формулу (6) в виде формулы отрезков для линзы, можно ввести понятие фокусного расстояния f зонной пластинки Френеля:
Если на пути световой волны, исходящей от точечного источника S, поставить диафрагму, которая перекроет все четные или все нечетные зоны Френеля (Рис.8), то интенсивность света в точке А резко увеличится. Такая диафрагма действует подобно собирающей линзе и называется амплитудной зонной пластинкой Френеля. Представляя формулу (6) в виде формулы отрезков для линзы, можно ввести понятие фокусного расстояния f зонной пластинки Френеля: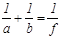 (7), где
(7), где 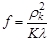 (8),
(8), 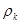 - радиус K – ой зоны Френеля K=(2 m+1)– нечетное число, m=0,1, 2, 3…
- радиус K – ой зоны Френеля K=(2 m+1)– нечетное число, m=0,1, 2, 3…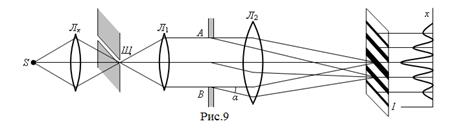
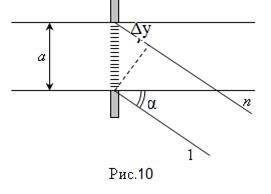 Каждую из этих полосок можно рассматривать как источник волн одинаковой амплитуды и фазы. Колебания, пришедшие на экран от каждой полоски, будем изображать коротким вектором
Каждую из этих полосок можно рассматривать как источник волн одинаковой амплитуды и фазы. Колебания, пришедшие на экран от каждой полоски, будем изображать коротким вектором 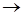 . Длина вектора отображает амплитуду колебаний, а его ориентация фазу колебаний. Если α=0, то колебания от всех участков щели придут
. Длина вектора отображает амплитуду колебаний, а его ориентация фазу колебаний. Если α=0, то колебания от всех участков щели придут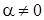 , тогда,
, тогда, 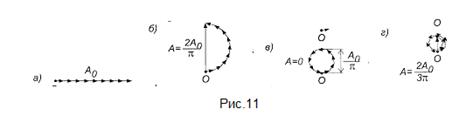 если фазу колебаний, пришедших от нижнего участка щели, принять за нуль, то колебания, пришедшие на экран от всех последующих участков, будут запаздывать по фазе и на векторной диаграмме каждый следующий вектор должен быть повернут относительно предыдущего вектора на небольшой угол. Разность хода между крайними лучами равна
если фазу колебаний, пришедших от нижнего участка щели, принять за нуль, то колебания, пришедшие на экран от всех последующих участков, будут запаздывать по фазе и на векторной диаграмме каждый следующий вектор должен быть повернут относительно предыдущего вектора на небольшой угол. Разность хода между крайними лучами равна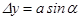 (9)
(9)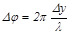 (10)
(10)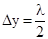 (т.е.
(т.е. 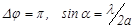 ), то это условие, в отличие от результата сложения двух колебаний, еще не приводит к минимуму (Рис.11б) и результирующая амплитуда равна
), то это условие, в отличие от результата сложения двух колебаний, еще не приводит к минимуму (Рис.11б) и результирующая амплитуда равна 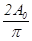 (равна диаметру полуокружности, длина которой А0).
(равна диаметру полуокружности, длина которой А0).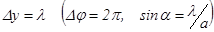 (рис.12в). Используя метод векторных диаграмм и формулы (9) и (10), получим следующую таблицу:
(рис.12в). Используя метод векторных диаграмм и формулы (9) и (10), получим следующую таблицу: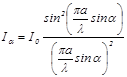 (11),
(11),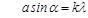 (12),
(12),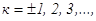 интенсивность света равна нулю. Таким образом, интенсивность равна нулю во всех случаях, когда разность хода Δy между крайними лучами равна λ, 2λ, 3λ, ……, кλ, т.е. минимумы освещенности соответствуют направлениям, для которых sinα =
интенсивность света равна нулю. Таким образом, интенсивность равна нулю во всех случаях, когда разность хода Δy между крайними лучами равна λ, 2λ, 3λ, ……, кλ, т.е. минимумы освещенности соответствуют направлениям, для которых sinα = 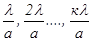 .
. 
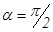 ), полосы исчезнут.
), полосы исчезнут.

 Задание 1. Зная длину волны лазерного излучения и радиус круглого отверстия в алюминиевой фольге, рассчитайте по формуле (6) при b>>a на каких расстояниях от точечного источника света следует установить отверстие, чтобы для центральной точки экрана Э в отверстии укладывалась одна зона, две зоны, три зоны Френеля. Результаты расчета проверьте экспериментально. Для моделирования точечного источника используйте He-Ne лазер (λ=0.63мкм) и короткофокусную рассеивающую линзу (f=1см) (Рис.15).
Задание 1. Зная длину волны лазерного излучения и радиус круглого отверстия в алюминиевой фольге, рассчитайте по формуле (6) при b>>a на каких расстояниях от точечного источника света следует установить отверстие, чтобы для центральной точки экрана Э в отверстии укладывалась одна зона, две зоны, три зоны Френеля. Результаты расчета проверьте экспериментально. Для моделирования точечного источника используйте He-Ne лазер (λ=0.63мкм) и короткофокусную рассеивающую линзу (f=1см) (Рис.15).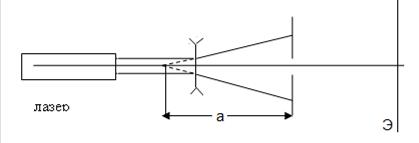
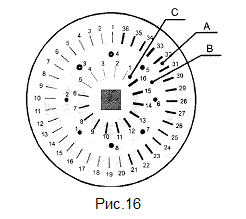 Для выполнения этого задания используйте He-Ne–лазер (λ=0.63мкм) и тест-объект МОЛ-01. Учебный демонстрационный тест-объект МОЛ-01 (Рис.16) представляет собой стеклянную подложку с зеркальным непрозрачным покрытием и с выполненными по специальной фотолитографической технологии прозрачными структурами (одиночные и двойные штрихи, круглые отверстия, кольца и т. д.). Они расположены в трех рядах А, В и С через равные угловые промежутки. Ряд А – двойные щели с переменным расстоянием между щелями d и шириной щели a. Ряд С – одинарные щели, ряд В- круглые отверстия, отверстия с центральным непрозрачным диском и зонная пластинка с диаметром первой открытой зоны 200мкм и общим числом зон 21. В центре квадратная сетка из прозрачных штрихов шириной 6 мкм и периодами 50 мкм по обеим координатам. Общее число штрихов по каждой координате – 100. Длина каждого штриха -5мм.
Для выполнения этого задания используйте He-Ne–лазер (λ=0.63мкм) и тест-объект МОЛ-01. Учебный демонстрационный тест-объект МОЛ-01 (Рис.16) представляет собой стеклянную подложку с зеркальным непрозрачным покрытием и с выполненными по специальной фотолитографической технологии прозрачными структурами (одиночные и двойные штрихи, круглые отверстия, кольца и т. д.). Они расположены в трех рядах А, В и С через равные угловые промежутки. Ряд А – двойные щели с переменным расстоянием между щелями d и шириной щели a. Ряд С – одинарные щели, ряд В- круглые отверстия, отверстия с центральным непрозрачным диском и зонная пластинка с диаметром первой открытой зоны 200мкм и общим числом зон 21. В центре квадратная сетка из прозрачных штрихов шириной 6 мкм и периодами 50 мкм по обеим координатам. Общее число штрихов по каждой координате – 100. Длина каждого штриха -5мм. , xk – координата k-ого дифракционного минимума, отсчитанная от центра дифракционной картины. Выполните измерения для щелей С1 и С15. Луч лазера непосредственно направьте на измеряемую щель. В случае измерения щели С1 установите расстояние r от тест-объекта до экрана равным (30 – 40) см, для щели С15 – (80 – 90) см. Обратите внимание, как ширина щели влияет на вид дифракционной картины. Оцените погрешность измерений.
, xk – координата k-ого дифракционного минимума, отсчитанная от центра дифракционной картины. Выполните измерения для щелей С1 и С15. Луч лазера непосредственно направьте на измеряемую щель. В случае измерения щели С1 установите расстояние r от тест-объекта до экрана равным (30 – 40) см, для щели С15 – (80 – 90) см. Обратите внимание, как ширина щели влияет на вид дифракционной картины. Оцените погрешность измерений.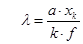 , (13)
, (13)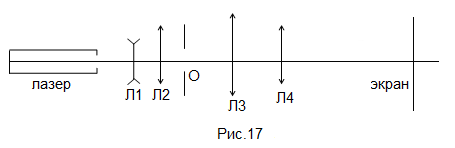


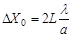 ,
,
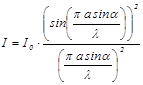 (14),
(14),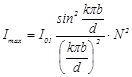 (15)
(15)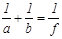 , (2)
, (2) 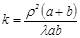 , (3)
, (3) 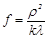 , (4)
, (4) 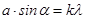 , (5)
, (5) 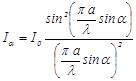 , (6)
, (6) 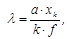 (7)
(7) 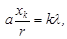
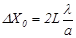 , (9)
, (9) 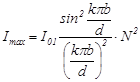 .
.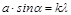 (4),
(4), 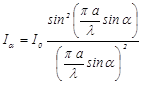 (5),
(5), 


