Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сведения из классической теории дисперсии веществаСодержание книги
Поиск на нашем сайте
ДИСПЕРСИЯ СВЕТА Цель работы: Научиться работать на гониометре, измерять с помощью гониометра показатель преломления вещества методом отклонения луча в призме, определять дисперсию вещества. Уметь демонстрировать призматические спектры большой аудитории.
Вопросы, знание которых необходимо для выполнения работы: § Нормальная и аномальная дисперсия. § Классическая электронная теория дисперсии света. § Ход лучей в призме, угол наименьшего отклонения. § Вывод рабочей формулы для определения показателя преломления. § Устройство и юстировка гониометра. § Методы измерения на гониометре преломляющего угла призмы. § Метод измерения наименьшего угла отклонения лучей призмой. § Дисперсия вещества, угловая дисперсия призмы, их определение. § Определение собственной частоты колебаний электронов.
Литература 1. Д.В. Сивухин. Общий курс физики. Оптика, т.3, §§84, 94, 2005. 2. Е.И. Бутиков. Оптика, §§ 2.3-2.5, 2003. 3. Настоящее руководство. Дополнительная литература
Угловая дисперсия призмы Угловая дисперсия призмы в окрестности длины волны λ измеряется величиной
где αmin – угол наименьшего отклонения лучей призмой. Так как угол отклонения α непосредственно зависит от показателя преломления стекла призмы n, а n, в свою очередь, зависит от λ, то угловую дисперсию можно представить в виде:
Используя выражения (15,16), найдем:
Как видно из формулы (18), угловая дисперсия призмы не зависит от ее размеров, а зависит лишь от преломляющего угла и материала, из которого сделана призма, т.е. от показателя преломления n вещества призмы. Как было отмечено выше, величина dn/dλ называется дисперсией вещества призмы. Эту величину можно найти графически, когда известны показатели преломления для ряда длин волн и построен график n=f(λ).
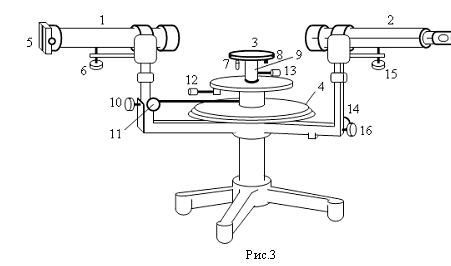
Описание гониометра Из предыдущих параграфов видно, что для определения n и dn/dλ нужно измерить преломляющий угол призмы и углы наименьшего отклонения лучей для разных длин волн. Прибор для точного измерения углов называется гониометром (рис. 3). Он состоит из следующих основных частей: 1 – коллиматора, 2 – зрительной трубы, 3 - столика с тремя установочными винтами. 4 – лимба с делениями и двумя нониусами, расположенными друг от друга под углом 180 градусов. Все основные узлы прибора смонтированы на треножном основании. Колонка коллиматора укреплена неподвижно, а зрительная труба вращается вокруг оси вместе с нониусами, которые скользят вдоль лимба. Коллиматор служит для получения параллельного пучка света.
На одном конце трубы коллиматора имеется объектив, с другой стороны вставлен патрубок с вертикальной щелью 5. Патрубок перемещается вдоль оси коллиматора. Ширина щели регулируется винтом. Внизу трубки коллиматора имеется винт 6, служащий для установки оси коллиматора в горизонтальной плоскости. Столик имеет два диска, три установочных винта 7, 8, 9, что дает возможность наклонять верхний диск относительно вертикальной оси. Винт 10, находящийся внизу колонки коллиматора, закрепляет столик. При закрепленном винте 10 столик может смешаться в небольших пределах с помощью микрометрического винта 11, расположенного сбоку колонки коллиматора рядом с винтом 10. Винт 12 скрепляет столик гониометра с лимбом для их совместного вращения. При освобождении винта 12 столик может вращаться без скрепления с лимбом. Столик можно поднимать или опускать и закреплять в желаемом положении. Зрительная труба 2 снабжена винтом 15, расположенным снизу трубы для установки ее оси в горизонтальной плоскости. Для закрепления трубы имеется винт 16, находящийся внизу колонки трубы. При закрепленном винте 16 трубу можно перемешать в небольших пределах микрометрическим винтом 14, находящимся сбоку колонки трубы. Зрительная труба снабжена автоколлимационным окуляром Гаусса с отверстием сбоку, назначение и устройство которого описывается ниже. Отсчет углов производится по обоим нониусам для исключения ошибки на эксцентриситет.
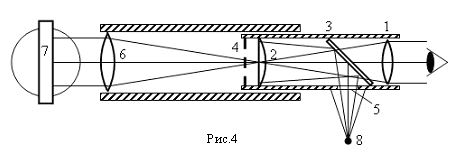
Установка гониометра. Гониометр требует тщательной установки: зрительная труба должна быть сфокусирована на бесконечность, щель коллиматора находиться в фокальной плоскости объектива коллиматора, оптические оси коллиматора и зрительной трубы должны быть перпендикулярны вертикальной оси вращения столика гониометра и находиться с ней в одной плоскости. Установка зрительной трубы гониометра на бесконечность. Грубо установку зрительной трубы на бесконечность можно осуществить, фокусируя ее на удаленный предмет. Точно эта операция выполняется автоколлимационным методом с помощью окуляра Гаусса, оптическая схема которого представлена на рис. 4. Окуляр Гаусса состоит из двух линз, полевой и глазной. Вблизи полевой линзы 2 в плоскости, которая должна быть совмещена с задней фокальной плоскостью объектива зрительной трубы, помещены две нити, натянутые в виде креста 4. Между линзами окуляра под углом 45° к оси трубы расположена стеклянная пластинка 3. Свет от источника 8. пройдя через боковое отверстие 5, отражается от пластинки 3 и освещает крест 4.
Предварительно перемещением глазной линзы 1 добиваются четкого изображения креста 4. Затем на столик гониометра устанавливают стойку с плоскопараллельной пластинкой. Лучи света, выходящие из зрительной трубы, отразятся от передней грани плоскопараллельной пластинки. Поворотом и изменением наклона трубы (или столика) добиваются попадания отраженных лучей обратно в зрительную трубу. В поле зрения зрительной трубы появится светлое расплывчатое пятно. Перемещением окуляра добиваются четкого изображения отражения креста от плоскопараллельной пластинки. При этом плоскости, в которых расположены крест и его изображение, совместятся и совпадут с задней фокальной плоскостью объектива. Таким образом, зрительная труба будет установлена на бесконечность. Установка оси трубы перпендикулярно оси вращения прибора. Установка оси зрительной трубы перпендикулярно оси вращения прибора осуществляется путем совмещения изображения креста с самим крестом. Для этого получают в зрительной трубе два изображения креста: вначале от одной грани, а затем, повернув столик на 180° и при необходимости изменяя наклон зрительной трубы, от другой грани плоскопараллельной пластинки. Если оба изображения окажутся смещенными в одну сторону (вверх или вниз) относительно креста, то совмещения можно добиться изменением наклона трубы. Если изображения находятся по разные стороны креста, это означает, что плоскость столика не горизонтальна. В этом случае изменяют наклон столика настолько, чтобы изображение горизонтальной нити приблизилось к самой нити на половину первоначального расстояния. После этого поворачивают столик на 180° и повторяют предыдущую процедуру. Эту операцию повторяют до тех пор, пока несовпадение креста и его изображения по вертикали не станет менее 1 мм. После этого пластинку снимают со столика. Установка коллиматора. Щель коллиматора должна находиться в фокальной плоскости объектива коллиматора. Чтобы произвести правильную установку щели, поступают следующим образом. Освещая щель, ловят изображение щели зрительной трубой и, не нарушая установку трубы, добиваются резкого изображения щели, регулируя на коллиматоре положение патрубка со щелью. Для установки оси коллиматора перпендикулярно оси вращения гониометра винтом 15 наклоняют коллиматор так, чтобы в середине изображения (по вертикали) ярко освещенной щели находилась точка пересечения нитей креста окуляра.
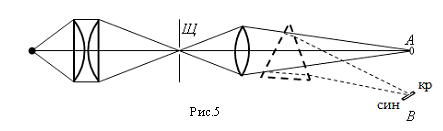
Задания и указания к их выполнению. Задание 1. В порядке предварительного упражнения соберите из отдельных деталей оптическую установку для проектирования сплошного спектра на большой экран. Для этой цели используйте школьную оптическую скамью. Схема установки представлена на (Рис.5).
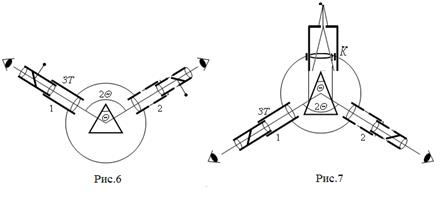
Сначала линзой сфокусируйте на экран "белое" изображение щели Щ, а затем, поставив на пути лучей призму в положение наименьшего отклонения, получите спектр В. Рис.5 Задание 2. Произведите установку гониометра, руководствуясь настоящим описанием. Задание 3. Определите преломляющий угол призмы. С помощью гониометра преломляющий угол призмы можно определить двумя способами, суть которых ясна из рисунков 6 и 7.
Задание 4. Определите показатель преломления материала призмы для различных длин волн линий излучения ртути. Для выполнения этого задания необходимо определить угол наименьшего отклонения для нескольких линий излучения ртути и, пользуясь формулой (16), вычислить показатель преломления для различных длин волн. Ртутная лампа расположена перед щелью коллиматора. Включите тумблер для зажигания ртутной лампы. Регулируя на коллиматоре положение патрубка со щелью, добейтесь четкого изображения щели коллиматора в зрительной трубе. Столик с призмой поверните так, чтобы направление пучка света из коллиматора составляло острый угол с гранью, обращенной к коллиматору. Далее найдите спектр невооруженным глазом, направляя глаз приблизительно по направлению выходящего из призмы пучка света и поворачивая столик с призмой на малые углы. Закрепив столик с призмой, наведите нити окуляра зрительной трубы на желтую линию и закрепите зрительную трубу. Освободите столик, поворачивая его вместе с призмой в ту или другую сторону, наблюдайте, куда движется спектральная линия. Столик с призмой следует вращать так, чтобы спектральная линия приближалась к направлению не отклоненного луча, при этом линия может выйти из поля зрения трубы. В этом случае открепляют зажимной винт трубы и, продолжая вращать столик с призмой, в том же направлении ведут трубу вслед за линией. Пройдя некоторое расстояние, линия остановится, а затем начнет двигаться в обратном направлении. В этот момент призма установлена в положение, соответствующее углу наименьшего отклонения для желтой линии ртути. Столик с призмой закрепляют и, вращая трубу, совмещают крест нити в окуляре с наблюдаемой линией. После этого, закрепив трубу, слегка поворачивайте столик с призмой, чтобы убедиться, соответствует ли установка призмы углу наименьшего отклонения. Если окажется, что линия при вращении немного сошла с нитей в сторону уменьшения отклонения, то исправьте установку на наименьшее отклонение и, закрепив столик с призмой, вновь наведите линию на крест нитей окуляра трубы. Закрепив окончательно столик и зрительную трубу, произведите отсчет по лимбу и двум нониусам. Аналогичные измерения произведите для всех остальных линий излучения ртути. Затем снимите призму со столика и поверните зрительную трубу так, чтобы непосредственно видеть щель коллиматора. Наведите изображение щели на крест нитей в окуляре трубы. Закрепите зрительную трубу, и вновь сделайте отсчет по лимбу и двум нониусам. Из полученных результатов измерений найдите для наблюдаемых спектральных линий значение угла наименьшего отклонения и определите показатель преломления стекла призмы для соответствующих длин волн. Задание 5. Определив длины волн линий излучения ртути по справочнику и используя данные, полученные в предыдущем задании, постройте график зависимости показателя преломления от длины волны. Из графика найдите дисперсию стекла призмы dn/dλ и по формуле (18) угловую дисперсию призмы для точек, соответствующих линиям излучения ртути. Полученные результаты занесите в таблицу:
Задание 6. Определить основной микроскопический параметр (собственную частоту колебаний электронов) ω0 для материала призмы. Для этого из таблицы, составленной по данным предыдущего задания, в формулу (13) поочередно подставьте два близких значения n и соответствующие им значения ω, а затем решите полученную систему уравнений относительно ω0. Для получения зачета необходимо: 1. Уметь демонстрировать призматический спектр на большом экране, проверять юстировку гониометра, выполнять на нем измерения преломляющего угла призмы и угла наименьшего отклонения спектральных линий в призматическом спектре. 2. Представить отчёт по выполненной работе. 3. Уметь отвечать на вопросы типа: · Какой физический смысл имеет показатель преломления вещества? · Что понимают под дисперсией вещества? · Ход лучей в трехгранной призме. · Нормальная и аномальная дисперсия. · Какие представления лежат в основе классической теории дисперсии света? · Почему оконное стекло не пропускает ультрафиолетовые лучи? Как в настоящей работе (1) зрительная труба устанавливается на бесконечность, (2) настраивается коллиматор, (3) поверхность столика гониометра устанавливается в горизонтальной плоскости, (4) оси коллиматора и зрительной трубы устанавливаются перпендикулярно оси вращения гониометра, (5) добиваются яркости и резкости изображения призматического спектра? Выберите правильный ответ:
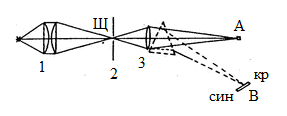
Для демонстрации призматического спектра на экране в настоящей работе предлагается собрать установку по следующей схеме:
Каково назначение элементов схемы (6) 1, (7) 2, (8) 3? Выберите правильный ответ: 1. Для получения параллельного пучка света. 2. Используется в качестве конденсора. 3. Для получения изображения призматического спектра в виде цветного изображения щели. 4. Для получения четкого изображения щели. 5. Правильного ответа нет.
Тест 3 (1). Какие задания необходимо выполнить в настоящей работе? (2). Что называют дисперсией вещества? (3). Что называют угловой дисперсией призмы? (4). Как можно из эксперимента найти дисперсию вещества? (5). Как в настоящей работе определяется показатель преломления стекла призмы? (6). От чего зависит угол отклонения луча призмой? (7). От чего зависит показатель преломления стекла призмы? (8). От чего зависит угловая дисперсия призмы? (9). При каком условии справедлива формула (1)?
(10). Что в формуле (1) обозначено как w0? Выберите правильный ответ:
РАБОТА 8 ПОЛЯРИЗАЦИЯ СВЕТА
Цель работы: Научиться демонстрировать и объяснять опыты с поляризованным светом, проводить анализ поляризованного света; выполнять экспериментальную проверку закона Малюса, закона Брюстера; познакомиться с принципом действия поляриметра, измерять в водном растворе концентрацию сахара. Вопросы, знание которых необходимо для выполнения работы:
· Поляризованный свет. Виды поляризации. · Поляризация света при отражении и преломлении. Формулы Френеля.
Рекомендуемая литература 1. Е.И. Бутиков. Оптика. §§ 4.1–4.5, 2003. 2. Сивухин Д.В. Общий курс физики. Оптика. §§ 62, 65, 75-79, 90-95, 2005. 3. Настоящее руководство Дополнительная литература 1. Ландсберг Г.С. Оптика. §§ 6, 101-112, 135, 136, 142- 148, 150-153, 163-164, 167-169, 1976. 2. Савельев И.В. Кypс общей физики. Т.З. §§ 28-34, 1971. 3. Фриш С.Е., Тиморева А.В. Курс общей физики. Т.З. §§ 258, 276, 277, 285-291, 291-296, 1957.
Краткие сведения из теории. Термин "поляризация света" был введен в науку Ньютоном для характеристики "полярности" светового луча, т.е. направлений преимущественного действия светового луча в плоскости, перпендикулярной направлению его распространения. С точки зрения электромагнитной теории поляризация света обусловлена поперечностью электромагнитных волн и отражает наличие у световых волн поперечной анизотропии, т. е. неэквивалентности направлений, в которых происходят колебания электрического (E) и магнитного (B) полей. Обычный, естественный свет представляет собой совокупность большого множества цугов волн, испускаемых возбужденными атомами макроскопического источника. Так как колебания поля в разных цугах естественного света абсолютно не согласованы, в естественном свете равноправны любые направления колебаний. Поэтому естественный свет абсолютно не поляризован, у него полностью отсутствует поперечная анизотропия. "Полярность действия", света проявляется, когда колебания электрического поля, Е (а значит и магнитного поля, H) каким-либо образом упорядочены. Свет, в котором колебания электрического поля (Е) происходят в одном направлении, называется линейно или плоско поляризованным (Рис.1).
Для удобства анализа взаимодействия света с веществом луч света обычно представляют как совокупность двух линейно поляризованных компонент с взаимно перпендикулярными колебаниями. На рис.2 приведены примеры различных поляризационных состояний светового луча при различных разностях фаз между взаимно перпендикулярными компонентами. Сдвиг по фазе между этими компонентами для естественного света непрерывно меняется, т. е. относительно друг друга они абсолютно не когерентны (Рис.2а). Если сдвиг по фазе δφ между взаимно перпендикулярными компонентами
Если сдвиг по фазе изменяется, но обнаруживает некоторые преимущественные значения, свет будет частично поляризован (Рис.2ж). Закон Малюса Если естественный свет пропустить через поляроид, то он станет линейно поляризованным. Вращение поляроида вокруг нормально падающего на него луча не будет влиять на интенсивность прошедшего света. Этот результат подтверждает абсолютную неполяризованность естественного света, который можно представить как любую совокупность двух равных по интенсивности линейно поляризованных некогерентных волн (с произвольной ориентацией в пространстве взаимно перпендикулярных компонент колебаний). При любой ориентации поляроида интенсивность прошедшего света будет составлять 0,5I0, где I0 - интенсивность естественного света, падающего на поляроид. Здесь предполагается, что вторая компонента с колебаниями, параллельными оси поляроида, полностью проходит. Если за первым поляроидом поставить второй поляроид и поворачивать его относительно первого поляроида, то интенсивность света, прошедшего через второй поляроид, будет зависеть от угла α между осями поляроидов.
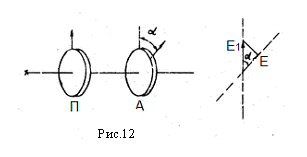
При скрещенных поляроидах (α=p/2) свет через второй поляроид не проходит. Рассматриваемый эффект легко объяснить, если представить линейно поляризованный свет как совокупность двух компонент с колебаниями параллельными и перпендикулярными оси второго поляроида (Рис.12). Второй поляроид пропустит только параллельную компоненту, для которой Е= E1Cos α. Так как интенсивность света пропорциональна квадрату амплитуды колебаний в волне, то интенсивность света I2, прошедшего через второй поляроид, будет зависеть от угла между осями поляроидов по закону (2): I 2 = I 1 cos 2 α здесь I1 - интенсивность линейно поляризованного света, вышедшего из первого поляроида. Формула (2) носит название закона Малюса.
Задания и указания к выполнению Задания, обозначенные *, выносятся на экзамен. Номера заданий, которые следует выполнять, называет преподаватель.
Задание 1*. Пронаблюдайте субъективным методом эффект скрещивания поляроидов (Рис.19). Продемонстрируйте этот же эффект на экране с помощью проекционной системы, установив в плоскостях I и 2 (Рис.20) поляроиды во вращающихся держателях. Чтобы не повредить поляроид, за конденсором обязательно установите тепловой фильтр. Задание2. Пронаблюдайте субъективно и продемонстрируйте на экране действие стопы, заменив в предыдущих установках один из поляроидов стопой. Задание 3*. Пронаблюдайте двойное лучепреломление, рассматривая какой-либо текст через положенный на него кристалл исландского шпата. Для демонстрации двойного лучепреломления на экране установите в плоскости I (Рис.20) точечную диафрагму и сразу за ней кристалл исландского шпата. На экране должно получиться два изображения диафрагмы. При повороте кристалла одно из изображений диафрагмы должно вращаться вокруг второго, неподвижного изображения. Установите в плоскости 2 вращающийся поляроид и покажите, что обыкновенный и необыкновенный лучи поляризованы во взаимно-перпендикулярных плоскостях. Задание 4*. Продемонстрируйте интерференцию поляризованных лучей. Для этого установите после конденсора и теплового фильтра поляроид, за ним анизотропный образец (целлофановую пленку) и перемещением объектива 0 (Рис.20) сфокусируйте поверхность образца на экран. Затем в плоскости 2 установите второй поляроид. Покажите, что при полном повороте поляроида происходит смена цветов на дополнительные и несколько раз интерференционная картина исчезает. Задание 5. Замените целлофан моделью из плексигласа двутавровой балки, создайте в ней напряжение и спроектируйте интерференционную картину на экран. Обратите внимание, что при изменении механического напряжения изменится вид и окраска интерференционной картины. Почему это происходит?
Задание 8. Продемонстрируйте поляризацию лазерного излучения. Используя закон Брюстера, определите ориентацию плоскости поляризации лазерного излучения и оцените показатель преломления стеклянной пластинки. Для этого на оптическую скамью установите гелий-неоновый лазер и вращающийся столик с круговой шкалой, снабженной нониусом. На столик поместите плоскопараллельную стеклянную пластинку (Рис.22). Направьте луч лазера на стеклянную пластинку и наблюдайте за изменением интенсивности отраженного луча при повороте пластинки. Путем последовательных поворотов пластинки и лазера вокруг своей оси Вы можете добиться полного гашения светового пятна на экране (Рис.22). На основании этого опыта можно определить ориентацию плоскости поляризации лазерного луча и, используя закон Брюстера, найти показатель преломления стеклянной пластинки. Задание 9. Произвести количественную проверку закона Малюса, используя два поляроида и фотоэлемент с подсоединенным к нему гальванометром. Можно считать, что интенсивность света, падающего на фотоэлемент, пропорциональна силе тока гальванометра. Для проверки закона Малюса, а также для выполнения заданий 10 и 11 используется цилиндрическая приставка, внутри которой на входе неподвижно закреплен поляризатор. За поляризатором помещена фазовая слюдяная пластинка в четверть длины волны, за фазовой пластинкой на выходе находится анализатор. В качестве источника излучения используется гелий-неоновый лазер. Свет, вышедший из анализатора, попадает на фотоэлемент, соединенный с гальванометром. Поляризатор ориентирован так, что скрещенному положению поляризатора и анализатора на шкале анализатора соответствует отсчет 90°. Анализатор можно поворачивать на 360°, фазовую пластинку - на 180°. Чтобы посторонний свет не попадал на фотоэлемент его надо располагать вплотную к анализатору. Выполняйте задание в следующем порядке: совместите указатель круговой шкалы анализатора со значением угла 90° и поворотом фазовой пластики добейтесь, чтобы показания гальванометра i0 были минимальны (как в этом случае должна быть ориентирована оптическая ось фазовой пластинки относительно оси поляризатора?). Затем поворотом анализатора в нулевое положение по угловой шкале установите поляризатор и анализатор параллельно друг другу и начинайте проверку закона Малюса. При параллельных поляроидах (α=0) интенсивность света и, соответственно, показания гальванометра наибольшие. Записав imax, поверните анализатор на 360°, записывая в таблицу показания гальванометра через каждые 15°. В окрестности минимумов и максимумов измерение выполняйте особенно тщательно, повторив их несколько раз. Закончив измерения, наденьте на фотоэлемент светозащитную крышку. Результаты измерений представьте в виде графика, по оси X которого отложен угол α, по оси У – отношение i0 - поправка на "темновой ток" фотоэлемента. На этом же графике по оси У отложите cos2α и сравните экспериментальную и теоретическую кривые. На миллиметровой бумаге в полярных координатах постройте график зависимости i=f(α). Радиус-векторы проводите длиной ~50 мм через каждые 15°. Должна получиться полярная диаграмма, характерная для линейно поляризованного света. Задание 10. Получите циркулярно поляризованный свет и исследуйте его полярную диаграмму. Для этого поверните фазовую пластинку на 450. Если оптическая ось фазовой пластинки параллельна или перпендикулярна оси поляризатора, то в этом случае в фазовой пластинке возбуждается только одна волна, необыкновенная или обыкновенная, соответственно. При выходе из фазовой пластинки свет остается линейно-поляризованным и его можно погасить анализатором. Следовательно, если скрестить анализатор с поляризатором (установить на лимбе отсчет 90°), затем поворотом фазовой пластинки добиться гашения света, то оптическая ось будет ориентирована, либо параллельно, либо перпендикулярно оси поляризатора. Если теперь повернуть пластинку на 45°относительно этого положения, ее ось составит 45° с осью поляризатора, и из фазовой пластинки должен выйти циркулярно-поляризованный свет. Поворачивая анализатор, измерьте фототок через каждые 15° на протяжении полного оборота от 0 до 360°. Постройте и исследуйте полярную диаграмму зависимости показаний гальванометра от угла поворота анализатора. Задание 11. Получите эллиптически поляризованный свет и исследуйте его полярную диаграмму. Используя описанную выше установку для преобразования линейно поляризованного света в циркулярно поляризованный, легко получить эллиптически поляризованный свет. Для этого достаточно нарушить соотношение амплитуд, изменив угол между оптической осью фазовой пластинки и осью поляризатора, так чтобы он имел промежуточное значение, не равное Задание 12. С помощью полутеневого поляриметра определите удельное вращение раствора сахара. Для этого вначале установите зрительную трубу поляриметра без трубки с оптически активным раствором на резкое изображение линии раздела полей. Вращением ручки анализатора, расположенной справа от окуляра, добейтесь равенства яркостей полей сравнения в чувствительном положении (вблизи полного затемнения поля зрения). Снимите по любой шкале лимба с нониусом отсчет Y0. Если необходимо, сделайте поправку на положение нуля. Поместите между поляризатором и анализатором поляриметра трубку с раствором сахара известной концентрации. Поворотом анализатора снова добейтесь одинакового затемнения всего поля зрения. Снимите отсчет по угловой шкале. Полученную разность отсчетов используйте для вычисления удельного вращения [α]. Затем, используя полученное значение удельного вращения, определите с помощью поляриметра концентрацию сахара в неизвестном растворе:
Для получения зачета необходимо: 1. Уметь: демонстрировать закон Малюса, закон Брюстера, двойное лучепреломление, интерференцию поляризованных лучей, оптическую активность водного раствора сахара. 2. Представить отчёт по выполненной работе. 3. Уметь отвечать на вопросы:
РАБОТА 9 ИНТЕРФЕРЕНЦИЯ СВЕТА
Цель работы: Приобретение умений, необходимых для демонстрации явления интерференции света; использовать интерференционную картину для выполнения измерений длины волны, расстояния между щелями в опыте Юнга, радиуса кривизны сферической поверхности. Вопросы, знание которых обязательно для допуска к выполнению работы
Литература
Дополнительная литература
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.111 (0.012 с.) |

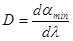 (17),
(17),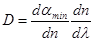 (17а)
(17а)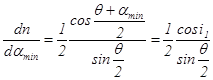 , или
, или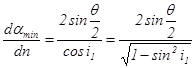
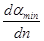 в формулу (17а), можно представить угловую дисперсию призмы вблизи положения наименьшего отклонения в виде (18):
в формулу (17а), можно представить угловую дисперсию призмы вблизи положения наименьшего отклонения в виде (18):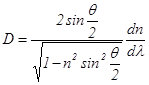 (18)
(18)
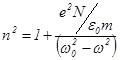 L (1)
L (1)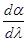 , характеризующий степень растянутости спектра.
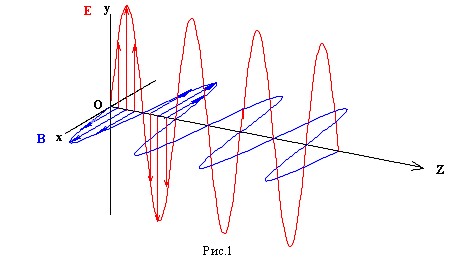
, характеризующий степень растянутости спектра.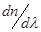 .
.
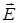 остается постоянным во времени, свет будет полностью поляризован, в общем случае эллиптически: проекция траектории конца вектора
остается постоянным во времени, свет будет полностью поляризован, в общем случае эллиптически: проекция траектории конца вектора 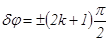 и равных амплитудах взаимно перпендикулярных компонент световая волна - циркулярно поляризована (Рис.2г).
и равных амплитудах взаимно перпендикулярных компонент световая волна - циркулярно поляризована (Рис.2г).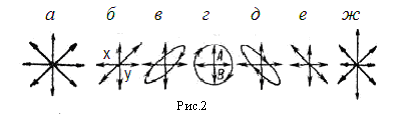
 (2),
(2),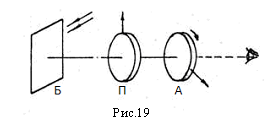 Поляризацию света можно наблюдать, рассматривая источник света через поляризационные приборы. При этом источник света не должен быть ярким. Это может быть освещенная бумага, свет из окна и т.п. На рис.19 показано расположение освещенной бумаги, поляроидов П, А и глаза для наблюдения исчезновения света при скрещивании поляроидов. Для демонстрации поляризации света большой аудитории необходимо использовать проекционную систему, состоящую из яркого источника света в кожухе, конденсора и объектива (Рис.20). Прежде всего, следует отцентрировать эту систему на оптической скамье. Расстояние КО должно быть немного больше фокусного расстояния объектива. Расстояние ЛК должно быть таким, чтобы изображение источника света получалось в месте расположения объектива. При таком расположении на экране получается яркое изображение.
Поляризацию света можно наблюдать, рассматривая источник света через поляризационные приборы. При этом источник света не должен быть ярким. Это может быть освещенная бумага, свет из окна и т.п. На рис.19 показано расположение освещенной бумаги, поляроидов П, А и глаза для наблюдения исчезновения света при скрещивании поляроидов. Для демонстрации поляризации света большой аудитории необходимо использовать проекционную систему, состоящую из яркого источника света в кожухе, конденсора и объектива (Рис.20). Прежде всего, следует отцентрировать эту систему на оптической скамье. Расстояние КО должно быть немного больше фокусного расстояния объектива. Расстояние ЛК должно быть таким, чтобы изображение источника света получалось в месте расположения объектива. При таком расположении на экране получается яркое изображение.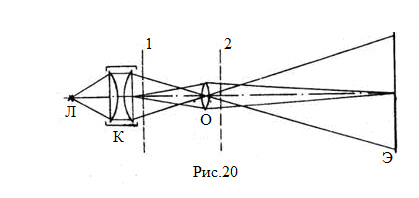
 Задание 6. Продемонстрируйте оптическую активность водного раствора сахара. Для этого между первым поляроидом (плоскость I) и объективом 0 (Рис.20) поместите кювету с водным раствором сахара. За объективом установите второй поляроид и экран.
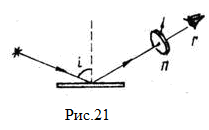
Задание 6. Продемонстрируйте оптическую активность водного раствора сахара. Для этого между первым поляроидом (плоскость I) и объективом 0 (Рис.20) поместите кювету с водным раствором сахара. За объективом установите второй поляроид и экран.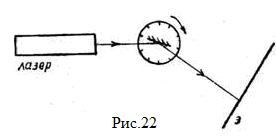 Задание 7. Пронаблюдайте поляризацию при отражении света под углами, близкими к углу Брюстера. Для субъективного наблюдения положите на стол стеклянную пластинку и через поляроид наблюдайте отражение в стекле неяркой лампочки (Рис.21). Вращая поляроид, исследуйте, является ли отраженный свет линейно поляризованным. Подберите оптимальный угол зрения.
Задание 7. Пронаблюдайте поляризацию при отражении света под углами, близкими к углу Брюстера. Для субъективного наблюдения положите на стол стеклянную пластинку и через поляроид наблюдайте отражение в стекле неяркой лампочки (Рис.21). Вращая поляроид, исследуйте, является ли отраженный свет линейно поляризованным. Подберите оптимальный угол зрения.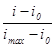 , равное отношению показаний гальванометра при данном угле α к максимальному значению тока.
, равное отношению показаний гальванометра при данном угле α к максимальному значению тока.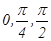 . Постройте и исследуйте полярную диаграмму зависимости показаний гальванометра от угла поворота анализатора.
. Постройте и исследуйте полярную диаграмму зависимости показаний гальванометра от угла поворота анализатора.