Поляризации света при, отражении и преломлении. Закон Брюстера .
 Естественный свет может стать линейно поляризованным в результате отражения от поверхности стекла или другого диэлектрика. Степень поляризации отраженного и преломленного лучей зависит от угла падения и описывается формулами Френеля. Из формул Френеля следует, что отраженный луч полностью поляризуется, если тангенс угла падения равен относительному показателю преломления диэлектрика, от поверхности которого происходит отражение: Естественный свет может стать линейно поляризованным в результате отражения от поверхности стекла или другого диэлектрика. Степень поляризации отраженного и преломленного лучей зависит от угла падения и описывается формулами Френеля. Из формул Френеля следует, что отраженный луч полностью поляризуется, если тангенс угла падения равен относительному показателю преломления диэлектрика, от поверхности которого происходит отражение:
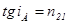 , (1) , (1)
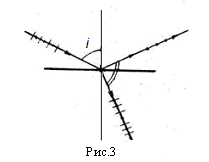
Формула (1) выражает закон Брюстера, где iБ - угол Брюстера. Легко показать, что при условии (1) угол между отраженным и преломленным лучами равен 90° (Рис.3). Колебания электрического поля в волне, отраженной под углом Брюстера, происходят перпендикулярно плоскости падения.
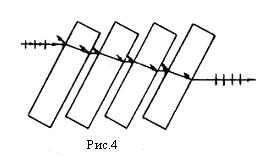 Для увеличения степени поляризации преломленных лучей используется стопа Столетова, которая состоит из 10-16 тонких стеклянных пластин, параллельных, друг другу и разделенных воздушным зазором (Рис.4). Свет направляется на стопу под углом Брюстера. Вследствие многократных отражений практически полностью отфильтровывается компонента с колебаниями, перпендикулярными плоскости падения, и прошедший через стопу свет оказывается линейно поляризован в плоскости падения. Для увеличения степени поляризации преломленных лучей используется стопа Столетова, которая состоит из 10-16 тонких стеклянных пластин, параллельных, друг другу и разделенных воздушным зазором (Рис.4). Свет направляется на стопу под углом Брюстера. Вследствие многократных отражений практически полностью отфильтровывается компонента с колебаниями, перпендикулярными плоскости падения, и прошедший через стопу свет оказывается линейно поляризован в плоскости падения.
Распространение света в анизотропной среде. Двойное лучепреломление. Дихроизм.
В анизотропной среде физические свойства зависят от направления. При этом оптические свойства анизотропных кристаллов зависят от ориентации направления колебаний светового вектора 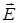 по отношению к оптической оси кристалла. Оптическая ось - направления, относительно которых кристалл обладает симметрией вращения. В природе существуют одноосные и двуосные оптические кристаллы. Наибольшее практическое применение имеют одноосные кристаллы, например, кварц, исландский шпат и др. по отношению к оптической оси кристалла. Оптическая ось - направления, относительно которых кристалл обладает симметрией вращения. В природе существуют одноосные и двуосные оптические кристаллы. Наибольшее практическое применение имеют одноосные кристаллы, например, кварц, исландский шпат и др.
С точки зрения классической теории Лоренца взаимодействие электромагнитной волны с веществом заключается в том, что электроны начинают осциллировать с частотой поля. Амплитуда вынужденных колебаний электронов зависит от соотношения частоты света и собственной частоты колебаний электронов. Так как в анизотропной среде силы связей электронов с атомами зависят от направления, то от направления колебаний, т.е. от ориентации светового вектора 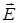 , будет зависеть разность между частотой собственных колебаний электронов w0 и частотой вынужденных колебаний w. Следовательно, от ориентации светового вектора , будет зависеть разность между частотой собственных колебаний электронов w0 и частотой вынужденных колебаний w. Следовательно, от ориентации светового вектора 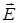 будет зависеть амплитуда вынужденных колебаний электронов. будет зависеть амплитуда вынужденных колебаний электронов.
Смещение электронов, колеблющихся под действием поля световой волны, приводит к поляризации среды, одной из макроскопических характеристик которой является диэлектрическая проницаемость ε. Таким образом, от ориентации светового вектора 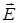 будет зависеть поляризуемость среды ε, а, следовательно, показатель преломления будет зависеть поляризуемость среды ε, а, следовательно, показатель преломления 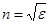 и скорость распространения света и скорость распространения света 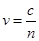 . .
 В случае одноосных оптических кристаллов диэлектрическая проницаемость ε является тензором второго ранга, содержащим две компоненты: e^ и В случае одноосных оптических кристаллов диэлектрическая проницаемость ε является тензором второго ранга, содержащим две компоненты: e^ и 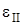 . Компонента e^ характеризует распространение света с колебаниями . Компонента e^ характеризует распространение света с колебаниями 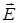 , перпендикулярными оптической оси кристалла, , перпендикулярными оптической оси кристалла, 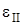 - определяет скорость распространения света с колебаниями - определяет скорость распространения света с колебаниями 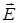 , параллельными оптической оси. , параллельными оптической оси.
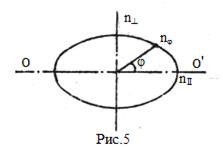
Зависимость показателя преломления от угла j между направлением колебаний 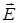 в электромагнитной волне и оптической осью кристалла изображается с помощью оптической индикатриссы (Рис.5). Длина радиус-векторов, проведенных из центра индикатриссы до пересечения с ее поверхностью, пропорциональна показателю преломления n j: n ^ соответствует волне с колебаниями в электромагнитной волне и оптической осью кристалла изображается с помощью оптической индикатриссы (Рис.5). Длина радиус-векторов, проведенных из центра индикатриссы до пересечения с ее поверхностью, пропорциональна показателю преломления n j: n ^ соответствует волне с колебаниями 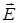 , перпендикулярными оптической оси, , перпендикулярными оптической оси, 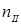 - колебаниям вектора - колебаниям вектора 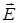 , параллельным оптической оси. В одноосных кристаллах индикатрисса имеет вид эллипсоида вращения, в котором оптическая ось совпадает с осью эллипсоида вращения кристалла. , параллельным оптической оси. В одноосных кристаллах индикатрисса имеет вид эллипсоида вращения, в котором оптическая ось совпадает с осью эллипсоида вращения кристалла.
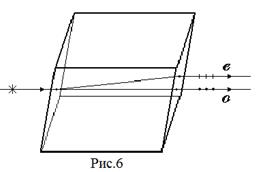 При прохождении света через оптический кристалл, при определенной ориентации кристалла, вследствие зависимости скорости света от направления колебаний вектора При прохождении света через оптический кристалл, при определенной ориентации кристалла, вследствие зависимости скорости света от направления колебаний вектора 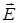 , наблюдается двойное лучепреломление: происходит раздвоение исходного луча на обыкновенный и необыкновенный (Рис.6). Обыкновенный и необыкновенный лучи линейно поляризованы во взаимно перпендикулярных плоскостях. Колебания светового вектора , наблюдается двойное лучепреломление: происходит раздвоение исходного луча на обыкновенный и необыкновенный (Рис.6). Обыкновенный и необыкновенный лучи линейно поляризованы во взаимно перпендикулярных плоскостях. Колебания светового вектора 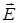 в обыкновенной волне перпендикулярны плоскости главного сечения кристалла, в необыкновенной волне - происходят в плоскости главного сечения. Под плоскостью главного сечения кристалла понимают плоскость, в которой лежит оптическая ось и нормаль к фронту волны. Поскольку колебания в обыкновенной волне перпендикулярны плоскости главного сечения кристалла, в необыкновенной волне - происходят в плоскости главного сечения. Под плоскостью главного сечения кристалла понимают плоскость, в которой лежит оптическая ось и нормаль к фронту волны. Поскольку колебания 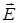 в необыкновенной волне происходят в плоскости главного сечения кристалла, то ее скорость будет зависеть от направления распространения, так как с изменением направления необыкновенной волны будет изменяться угол между вектором в необыкновенной волне происходят в плоскости главного сечения кристалла, то ее скорость будет зависеть от направления распространения, так как с изменением направления необыкновенной волны будет изменяться угол между вектором 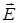 и оптической осью. По этой причине данная волна не подчиняется закону преломления, и получила название необыкновенной волны: для нее показатель преломления зависит от угла падения. и оптической осью. По этой причине данная волна не подчиняется закону преломления, и получила название необыкновенной волны: для нее показатель преломления зависит от угла падения.
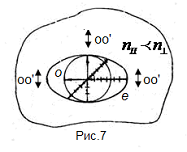 Мысленно поместим в анизотропную среду точечный источник естественного света. Колебаниями Мысленно поместим в анизотропную среду точечный источник естественного света. Колебаниями 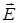 , перпендикулярные плоскости главного сечения кристалла, во всех направлениях будут распространяться с одной и той же скоростью: для всех направлений обыкновенной волны угол между оптической осью и направлением светового вектора , перпендикулярные плоскости главного сечения кристалла, во всех направлениях будут распространяться с одной и той же скоростью: для всех направлений обыкновенной волны угол между оптической осью и направлением светового вектора 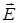 равен равен 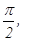 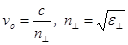 . Таким образом, фронт элементарной обыкновенной волны в одноосном кристалле является сферическим (рис.7). Фронт элементарной необыкновенной волны представляет собой эллипсоид вращения, ось вращения которого совпадает с оптической осью. В направлении оптической оси необыкновенная волна распространяется со скоростью . Таким образом, фронт элементарной обыкновенной волны в одноосном кристалле является сферическим (рис.7). Фронт элементарной необыкновенной волны представляет собой эллипсоид вращения, ось вращения которого совпадает с оптической осью. В направлении оптической оси необыкновенная волна распространяется со скоростью 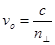 , т.к. колебания ее светового вектора для этого направления перпендикулярны оптической оси 00. В направлениях, перпендикулярных оптической оси, скорость распространения необыкновенной волны будет равной , т.к. колебания ее светового вектора для этого направления перпендикулярны оптической оси 00. В направлениях, перпендикулярных оптической оси, скорость распространения необыкновенной волны будет равной 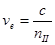 , где , где 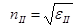 , так как для этих направлений распространения колебания светового вектора , так как для этих направлений распространения колебания светового вектора 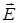 в необыкновенной волне параллельны оптической оси (Рис.7). В остальных направлениях скорость необыкновенной волны будет промежуточной между скоростями ve и vo. Таким образом, в направлении оптической оси обе волны, обыкновенная и необыкновенная, распространяются с одной и той же скоростью в необыкновенной волне параллельны оптической оси (Рис.7). В остальных направлениях скорость необыкновенной волны будет промежуточной между скоростями ve и vo. Таким образом, в направлении оптической оси обе волны, обыкновенная и необыкновенная, распространяются с одной и той же скоростью 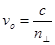 , и в этом направлении фронты обыкновенной и необыкновенной волн соприкасаются (Рис.7). В природе встречаются два случая: , и в этом направлении фронты обыкновенной и необыкновенной волн соприкасаются (Рис.7). В природе встречаются два случая: 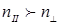 - положительные кристаллы; - положительные кристаллы; 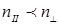 - отрицательные кристаллы. Для положительных кристаллов - отрицательные кристаллы. Для положительных кристаллов 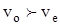 , для отрицательных , для отрицательных 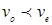 . .
Для построения фронта обыкновенной и необыкновенной волн в кристалле и хода обыкновенного и необыкновенного лучей можно воспользоваться принципом Гюйгенса.
 Согласно принципу Гюйгенса каждая точка исходного фронта волны является источником элементарных вторичных волн, огибающая фронтов элементарных вторичных волн представляет собой новый фронт волны. Согласно принципу Гюйгенса каждая точка исходного фронта волны является источником элементарных вторичных волн, огибающая фронтов элементарных вторичных волн представляет собой новый фронт волны.
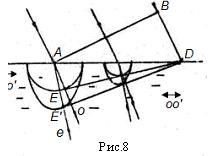
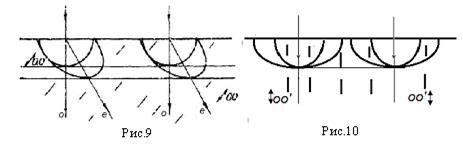
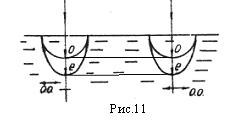
Пусть образец вырезан так, что оптическая ось лежит в плоскости падения и параллельна его поверхности, на которую под углом падает плоская монохроматическая волна (Рис.8). Фронт волны АВ достигает точки А раньше, чем точки D. Пока свет дойдет от точки В к точке D, из точки А во второй среде возникнут и распространятся на определенные расстояния вторичные обыкновенная и необыкновенная волны. Фронт элементарной обыкновенной волны - сферический, необыкновенной - эллипсоидальный. В направлении оптической оси обе вторичные волны распространяются с одной и той же скоростью, и в этом направлении их фронты соприкасаются. Если кристалл отрицателен (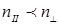 , , 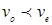 ) эллипсоидальный фронт необыкновенной волны будет вытянут в направлении, перпендикулярном оптической оси (Рис.8). Огибающая этих эллипсоидальных волн E'D представляет фронт необыкновенной волны в кристалле, который не совпадает с фронтом обыкновенной волны ED. Обыкновенный АЕ и необыкновенный АЕ' лучи в этом случае также не совпадают. Они проводятся через точку падения луча и точку касания огибающей с соответствующим фронтом вторичной волны. На рис. 9 и 10 выполнено аналогичное построение для случая нормального падения лучей, когда оптическая ось ориентирована наклонно к границе раздела (Рис.9) и когда волна распространяется вдоль оптической оси (Рис.10). В последнем случае, как видно из построения, двойного лучепреломления не происходит. Таким образом, оптическую ось можно выделить физически как систему направлений, вдоль которых не происходит двойного лучепреломления. ) эллипсоидальный фронт необыкновенной волны будет вытянут в направлении, перпендикулярном оптической оси (Рис.8). Огибающая этих эллипсоидальных волн E'D представляет фронт необыкновенной волны в кристалле, который не совпадает с фронтом обыкновенной волны ED. Обыкновенный АЕ и необыкновенный АЕ' лучи в этом случае также не совпадают. Они проводятся через точку падения луча и точку касания огибающей с соответствующим фронтом вторичной волны. На рис. 9 и 10 выполнено аналогичное построение для случая нормального падения лучей, когда оптическая ось ориентирована наклонно к границе раздела (Рис.9) и когда волна распространяется вдоль оптической оси (Рис.10). В последнем случае, как видно из построения, двойного лучепреломления не происходит. Таким образом, оптическую ось можно выделить физически как систему направлений, вдоль которых не происходит двойного лучепреломления.
 В случае, представленном на рис.11, оптическая ось параллельна поверхности кристалла, лучи распространяются перпендикулярно к оптической оси. Здесь также не происходит пространственного разделения луча на лучи обыкновенный и необыкновенный, хотя скорости распространения лучей разные. При выходе из кристалла между этими лучами возникает оптическая разность хода Δ=d(n0 – ne), где d - толщина кристалла, В случае, представленном на рис.11, оптическая ось параллельна поверхности кристалла, лучи распространяются перпендикулярно к оптической оси. Здесь также не происходит пространственного разделения луча на лучи обыкновенный и необыкновенный, хотя скорости распространения лучей разные. При выходе из кристалла между этими лучами возникает оптическая разность хода Δ=d(n0 – ne), где d - толщина кристалла, 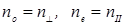 . .
Некоторые оптические кристаллы наряду с двойным лучепреломлением обладают дихроизмом - способностью поглощать свет с определенным направлением колебаний светового вектора 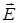 . Так, например, пластинка турмалина, вырезанная параллельно оптической оси, толщиной в 1 мм практически полностью поглощает обыкновенный луч и может быть использована для получения линейно поляризованного света. Аналогичным свойством обладают поляроиды, которые представляют собой совокупность одинаково ориентированных мелких кристалликов герапатита (сульфата йодистого хинина), впрессованных в целлулоидную пленку, заклеенную для защиты от механических повреждений и действия влаги между двумя прозрачными пластинками. Часто для изготовления поляроидов используют молекулярные поливиниленовые пленки, молекулы которых также обладают дихроизмом. Поляроиды дешевы и удобны в обращении. . Так, например, пластинка турмалина, вырезанная параллельно оптической оси, толщиной в 1 мм практически полностью поглощает обыкновенный луч и может быть использована для получения линейно поляризованного света. Аналогичным свойством обладают поляроиды, которые представляют собой совокупность одинаково ориентированных мелких кристалликов герапатита (сульфата йодистого хинина), впрессованных в целлулоидную пленку, заклеенную для защиты от механических повреждений и действия влаги между двумя прозрачными пластинками. Часто для изготовления поляроидов используют молекулярные поливиниленовые пленки, молекулы которых также обладают дихроизмом. Поляроиды дешевы и удобны в обращении.
Закон Малюса
Если естественный свет пропустить через поляроид, то он станет линейно поляризованным. Вращение поляроида вокруг нормально падающего на него луча не будет влиять на интенсивность прошедшего света. Этот результат подтверждает абсолютную неполяризованность естественного света, который можно представить как любую совокупность двух равных по интенсивности линейно поляризованных некогерентных волн (с произвольной ориентацией в пространстве взаимно перпендикулярных компонент колебаний). При любой ориентации поляроида интенсивность прошедшего света будет составлять 0,5I0, где I0 - интенсивность естественного света, падающего на поляроид. Здесь предполагается, что вторая компонента с колебаниями, параллельными оси поляроида, полностью проходит.
Если за первым поляроидом поставить второй поляроид и поворачивать его относительно первого поляроида, то интенсивность света, прошедшего через второй поляроид, будет зависеть от угла α между осями поляроидов.
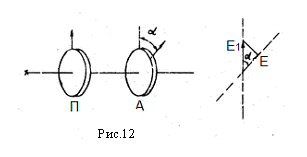
При скрещенных поляроидах (α=p/2) свет через второй поляроид не проходит. Рассматриваемый эффект легко объяснить, если представить линейно поляризованный свет как совокупность двух компонент с колебаниями параллельными и перпендикулярными оси второго поляроида (Рис.12).
Второй поляроид пропустит только параллельную компоненту, для которой Е= E1Cos α. Так как интенсивность света пропорциональна квадрату амплитуды колебаний в волне, то интенсивность света I2, прошедшего через второй поляроид, будет зависеть от угла между осями поляроидов по закону (2):
I 2 = I 1 cos 2 α  (2), (2),
здесь I1 - интенсивность линейно поляризованного света, вышедшего из первого поляроида. Формула (2) носит название закона Малюса.
|



 Естественный свет может стать линейно поляризованным в результате отражения от поверхности стекла или другого диэлектрика. Степень поляризации отраженного и преломленного лучей зависит от угла падения и описывается формулами Френеля. Из формул Френеля следует, что отраженный луч полностью поляризуется, если тангенс угла падения равен относительному показателю преломления диэлектрика, от поверхности которого происходит отражение:
Естественный свет может стать линейно поляризованным в результате отражения от поверхности стекла или другого диэлектрика. Степень поляризации отраженного и преломленного лучей зависит от угла падения и описывается формулами Френеля. Из формул Френеля следует, что отраженный луч полностью поляризуется, если тангенс угла падения равен относительному показателю преломления диэлектрика, от поверхности которого происходит отражение: 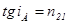 , (1)
, (1) Для увеличения степени поляризации преломленных лучей используется стопа Столетова, которая состоит из 10-16 тонких стеклянных пластин, параллельных, друг другу и разделенных воздушным зазором (Рис.4). Свет направляется на стопу под углом Брюстера. Вследствие многократных отражений практически полностью отфильтровывается компонента с колебаниями, перпендикулярными плоскости падения, и прошедший через стопу свет оказывается линейно поляризован в плоскости падения.
Для увеличения степени поляризации преломленных лучей используется стопа Столетова, которая состоит из 10-16 тонких стеклянных пластин, параллельных, друг другу и разделенных воздушным зазором (Рис.4). Свет направляется на стопу под углом Брюстера. Вследствие многократных отражений практически полностью отфильтровывается компонента с колебаниями, перпендикулярными плоскости падения, и прошедший через стопу свет оказывается линейно поляризован в плоскости падения.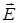 по отношению к оптической оси кристалла. Оптическая ось - направления, относительно которых кристалл обладает симметрией вращения. В природе существуют одноосные и двуосные оптические кристаллы. Наибольшее практическое применение имеют одноосные кристаллы, например, кварц, исландский шпат и др.
по отношению к оптической оси кристалла. Оптическая ось - направления, относительно которых кристалл обладает симметрией вращения. В природе существуют одноосные и двуосные оптические кристаллы. Наибольшее практическое применение имеют одноосные кристаллы, например, кварц, исландский шпат и др.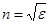 и скорость распространения света
и скорость распространения света 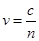 .
. В случае одноосных оптических кристаллов диэлектрическая проницаемость ε является тензором второго ранга, содержащим две компоненты: e^ и
В случае одноосных оптических кристаллов диэлектрическая проницаемость ε является тензором второго ранга, содержащим две компоненты: e^ и 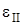 . Компонента e^ характеризует распространение света с колебаниями
. Компонента e^ характеризует распространение света с колебаниями 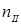 - колебаниям вектора
- колебаниям вектора  При прохождении света через оптический кристалл, при определенной ориентации кристалла, вследствие зависимости скорости света от направления колебаний вектора
При прохождении света через оптический кристалл, при определенной ориентации кристалла, вследствие зависимости скорости света от направления колебаний вектора  Мысленно поместим в анизотропную среду точечный источник естественного света. Колебаниями
Мысленно поместим в анизотропную среду точечный источник естественного света. Колебаниями 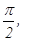
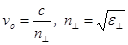 . Таким образом, фронт элементарной обыкновенной волны в одноосном кристалле является сферическим (рис.7). Фронт элементарной необыкновенной волны представляет собой эллипсоид вращения, ось вращения которого совпадает с оптической осью. В направлении оптической оси необыкновенная волна распространяется со скоростью
. Таким образом, фронт элементарной обыкновенной волны в одноосном кристалле является сферическим (рис.7). Фронт элементарной необыкновенной волны представляет собой эллипсоид вращения, ось вращения которого совпадает с оптической осью. В направлении оптической оси необыкновенная волна распространяется со скоростью 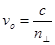 , т.к. колебания ее светового вектора для этого направления перпендикулярны оптической оси 00. В направлениях, перпендикулярных оптической оси, скорость распространения необыкновенной волны будет равной
, т.к. колебания ее светового вектора для этого направления перпендикулярны оптической оси 00. В направлениях, перпендикулярных оптической оси, скорость распространения необыкновенной волны будет равной 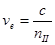 , где
, где 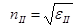 , так как для этих направлений распространения колебания светового вектора
, так как для этих направлений распространения колебания светового вектора 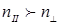 - положительные кристаллы;
- положительные кристаллы; 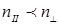 - отрицательные кристаллы. Для положительных кристаллов
- отрицательные кристаллы. Для положительных кристаллов 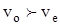 , для отрицательных
, для отрицательных 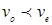 .
. Согласно принципу Гюйгенса каждая точка исходного фронта волны является источником элементарных вторичных волн, огибающая фронтов элементарных вторичных волн представляет собой новый фронт волны.
Согласно принципу Гюйгенса каждая точка исходного фронта волны является источником элементарных вторичных волн, огибающая фронтов элементарных вторичных волн представляет собой новый фронт волны.
 В случае, представленном на рис.11, оптическая ось параллельна поверхности кристалла, лучи распространяются перпендикулярно к оптической оси. Здесь также не происходит пространственного разделения луча на лучи обыкновенный и необыкновенный, хотя скорости распространения лучей разные. При выходе из кристалла между этими лучами возникает оптическая разность хода Δ=d(n0 – ne), где d - толщина кристалла,
В случае, представленном на рис.11, оптическая ось параллельна поверхности кристалла, лучи распространяются перпендикулярно к оптической оси. Здесь также не происходит пространственного разделения луча на лучи обыкновенный и необыкновенный, хотя скорости распространения лучей разные. При выходе из кристалла между этими лучами возникает оптическая разность хода Δ=d(n0 – ne), где d - толщина кристалла, 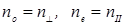 .
.
 (2),
(2),


