Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы получения интерференционной картины. Опыт Юнга.Содержание книги
Поиск на нашем сайте
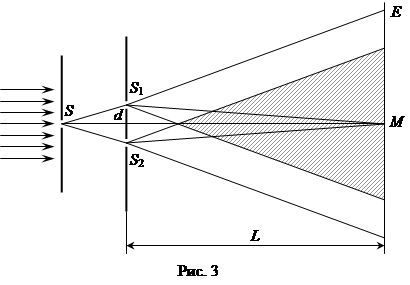
Один из методов получения интерференционной картины был предложен Юнгом в 1802 г. (Рис. 3). Источником света в этом опыте служит узкая ярко освещенная щель S. Прошедший через щель S свет вследствие дифракции образует расходящийся пучок, который падает на второй экран с двумя близко расположенными щелями S1 и S2. Таким образом, щели S1 и S2 освещаются различными участками фронта одной и той же световой волны. На основании принципа Гюйгенса – Френеля две щели можно рассматривать как когерентные источники. Увеличение ширины первой щели S неизбежно приводит к уменьшению пространственной когерентности излучения и, соответственно, к уменьшению контрастности (видности) интерференционных полос. В современной демонстрационной модификации опыта Юнга в качестве источника света используют лазер. При этом для когерентного возбуждения вторичных источников S1 и S2 необходимость во вспомогательном отверстии S отпадает, так как в лазерном излучении световые колебания когерентны по всему поперечному сечению пучка, и две щели вводят непосредственно в пучок лазерного излучения.
Измеряя ширину интерференционных полос, Юнг в 1802 г. впервые определил длину световых волн разного цвета. Для определения из интерференционной картины длины световой волны рассмотрим когерентные лучи S1M и S2M (Рис. 1), встречающиеся в точке М экрана, параллельного щелям. Если S1M = S1'M, то S2S1'= Δ – разность хода этих лучей. Из подобия треугольников S1S2S1' и NMO следует, что
где d - расстояние между центрами щелей. Так как d<< L, угол S2S1S1' очень ма и NM» L. Пусть в точке М наблюдается минимум k-ого порядка. Тогда
Отсюда получаем формулу для измерения длины:
здесь Бипризма Френеля
При демонстрации интерференции света с помощью бипризмы Френеля в данной работе используется школьная оптическая скамья, снабженная проекционным фонарем. Перед началом демонстрации необходимо поставить экран перпендикулярно световому пучку недалеко от бипризмы. Затем поворотом щели (или бипризмы) установить щель параллельно вертикальному ребру бипризмы. О правильности установки можно судить по виду светлой полосы на экране. Изменением ширины щели можно добиться наилучшей видимости интерференционных полос. Для получения более широких интерференционных полос следует поставить экран под углом к падающим на него лучам. Расстояние экрана от бипризмы влияет на ширину интерференционной полосы: чем больше это расстояние, тем шире, но зато слабее получаются полосы. Обратите внимание, как ширина щели влияет на качество интерференционной картины.
Для определения длины волны с помощью бипризмы Френеля в данной работе используется формула (15), где d - расстояние между мнимыми источниками S1 и S2, L - расстояние от плоскости, содержащей источники S1 и S2, до плоскости окулярного микрометра.
Кольца Ньютона Кольца Ньютона представляют собой один из видов интерференционных полос равной толщины. Они образуются при освещении сферической линзы, выпуклой поверхностью прижатой к плоскопараллельной стеклянной пластинке. Вблизи места соприкосновения поверхностей получается слой воздуха, толщина которого сравнима с длиной световой волны. В результате наложения лучей, отраженных от границ этого слоя, происходит интерференция.
Когерентными являются лучи, исходящие из одной и той же точки источника. На рис. 6 когерентные лучи обозначены цифрами 1 и 2. Лучи 1 и 2 практически параллельны, поскольку источник расположен в фокальной плоскости линзы. Между отраженными лучами 1' и 2' образуется оптическая разность хода
В опытах с кольцами Ньютона для получения отчетливой интерференционной картины в белом свете толщина воздушного слоя должна быть порядка нескольких микрометров. При этих условиях с достаточной точностью можно принять
На практике кольца Ньютона наблюдают либо невооруженным глазом, помещая его на пути лучей 1’ и 2' (Рис.6), либо в окуляр микроскопа, сфокусированного на интерференционную картину. Темное пятно в центре колец Ньютона в отраженном свете объясняется тем, что геометрическая разность хода между интерферирующими лучами в области точки 0 практически равна нулю, но имеет место потеря полдлины волны при отражении от поверхности линзы. При величине разности хода Δ между лучами 1' и 2'
где k = 0, 1, 2..., возникают темные кольца. Когда
- светлые кольца. По мере увеличения k кольца сближаются. Толщину воздушного слоя d можно связать с радиусом кольца, которому соответствует эта толщина. Из треугольника O`CD (Рис.6) для k – го кольца имеем:
где R - радиус кривизны линзы. Так как d<<R, то величиной d2 по сравнению с 2Rd можно пренебречь, тогда
Используя выражение (16) и (17), получим формулу для радиусов темных колец Ньютона в отраженном свете:
Зная длину волны λ, радиус кольца и порядок минимума, из формулы (20) можно найти радиус кривизны поверхности линзы. Однако вследствие упругой деформации стекла невозможно добиться идеального соприкосновения линзы и пластинки в точке касания. Поэтому более точный результат получится, если вычислять R из разности диаметров двух колец Dk и Dm:
Откуда
где m, k - номера темных колец, Dk, Dm - их диаметры, λ –длина волны используемого излучения.
Поэтому можно в качестве S применить ртутную лампу без вспомогательного экрана с малым отверстием, что обеспечивает значительный световой поток. С помощью листочка слюды (толщиной 0,03-0,05 мм) можно получить на экране яркую интерференционную картину. Чем тоньше пластинка, тем крупнее масштаб интерференционной картины, т.е. больше расстояние между полосами.
Задания и указания к выполнению Задания, обозначенные (*), выносятся на экзамен. Номера заданий, которые следует выполнять, называет преподаватель. Задание 1*. Продемонстрировать на экране интерференцию света с помощью бипризмы Френеля. Для этого воспользоваться школьной оптической скамьей и деталями из школьного набора по волновой оптике. Показать получившуюся на экране картину преподавателю. Задание 2. На оптической скамье, снабженной окулярным микрометром, по интерференционной картине, полученной с помощью бипризмы Френеля, измерить длину волны зеленого света. Для этого необходимо собрать установку, оптическая схема которой изображена на рис. 5. § Осветить щель, спроектировав на неё нить осветительной лампочки. Посмотрев через бипризму, убедиться в том, что она даёт два мнимых изображения щели. § Установить щель параллельно ребру бипризмы. § Сделать щель достаточно широкой и отцентрировать систему так, чтобы светлая вертикальная полоса попадала в окулярный микрометр. Для этого проверить ход световых лучей при помощи листа белой бумаги. § Поместить лист белой бумаги перед окулярным микрометром. Постепенно уменьшая ширину щели и слегка поворачивая ее вокруг горизонтальной оси, получить на бумаге интерференционную картину. § Наблюдая интерференционную картину через окулярный микрометр, посредством небольшого уменьшения щели добиться максимальной резкости интерференционных полос. § Установить перед окулярным микрометром интерференционный светофильтр. Пронаблюдать изменения в интерференционной картине. Закрепить все рейтеры на скамье и показать полученную интерференционную картину преподавателю или лаборанту. § Считая, что мнимые изображения щелей находятся в той же плоскости, что и сама щель, измерить расстояние L от щели до окулярного микрометра. § Для определения расстояния d между мнимыми изображениями щелей воспользоваться линзой с известным фокусным расстоянием f. Установить линзу между бипризмой и окулярным микрометром. Спроектировать с помощью линзы изображения
источников S1 и S2 на плоскость окулярного микрометра и измерить расстояние d` между изображениями S1' и S2' (Рис.8). § Настроить нить окуляра на одну из полос и снять показания окулярного микрометра. Сместить поле зрения на (k-m)=5 зеленых полос и опять снять показания микрометра. Найти z - разность этих показаний § По формуле (23) найти расстояние d между источниками:
здесь x1 - расстояние между линзой и плоскостью изображения источников. Подставляя это выражение в формулу (24), можно найти длину волны:
Оцените погрешность измерений.
Задание 4. Получите интерференционную картину от двух щелей с наименьшим расстоянием d (ряд А, № 1) и с наибольшим d (ряд А, № 36). Измерьте в обеих картинах ширину интерференционной полосы b. По формуле (25) найдите d расстояние между щелями: Оцените погрешность измерений. Задание 5. Продемонстрировать аудитории интерференционный опыт Поля с пластинкой слюды. В качестве источника света использовать ртутную лампу. Задание 6. Продемонстрировать большую временную когерентность лазерного излучения на примере интерференции лучей сферической волны, отраженных от толстой плоскопараллельной пластинки. Для преобразования лазерного излучения в сферическую волну используйте микро-объектив от микроскопа, в качестве экрана лист белой бумаги с отверстием, надетой на микро-объектив.
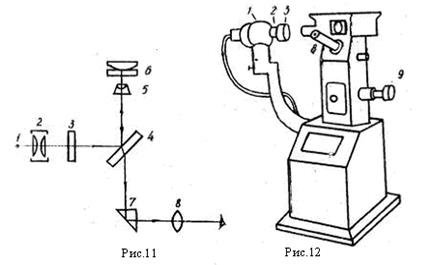
Задание 8. Определить по кольцам Ньютона радиус кривизны линзы. Для измерения диаметров интерференционных колец в настоящем задании используется вертикальный металлографический микроскоп МИМ-6. Упрощенная схема хода лучей и внешний вид микроскопа представлены на рисунках 11, 12. Цифры на этих рисунках соответствуют друг другу. Источник света 1 представляет собой металлическую трубку с вмонтированным гнездом для светодиода с одной стороны и гнездом для подключения источника постоянного тока с другой стороны. Напряжение, соответствующее нормальной работе осветителя, составляет 3В. При необходимости изменить цвет освещения достаточно сменить светодиод. В данном задании используется светодиод (λкр = 0,615 мкм), свет от которого
преобразуется в параллельный пучок конденсором 2. Попадая далее на полупрозрачную пластинку 4, свет отражается вверх, через объектив 5 освещает объект 6 (в данном случае пластинку и прижатую к ней линзу). Отраженный свет через объектив 5, поворотную призму 7 и окуляр 8 попадает на матрицу Веб - камеры, подключенной к компьютеру. На экране компьютера получается увеличенное изображение объекта. Для фокусировки, изменения расстояния от объектива до объекта, служит винт 9. Веб - камера крепится на микроскоп посредством резинового жгута, зажатого металлическим кольцом, закрепленным на трубке, предназначенной для окуляра. Такое крепление позволяет поворачивать плоскость наблюдения относительно оптической оси, не меняя положения самого объекта, а изменяя расположения камеры. Важным условием наблюдений является такое положение камеры, при котором видна наиболее освещенная часть объекта. При этом оптическая ось камеры совпадает с осью трубки, на которой крепится Веб - камера. В противном случае в объектив камеры попадает лишь часть исследуемого изображения. Выполнение задания можно разделить на четыре части:
Первые два пункта с целью определения соотношения между пикселями и микрометрами следует выполнить поочередно сначала для колец Ньютона, затем для объект - микрометра. Получение изображения интерференционной картины: § Включить компьютер. § Запустить программу работы с Веб камерой (Camera Plus). § В окне программы выбрать иконку Video Recorder. § Подключить питание к источнику света (светодиоду). § Установить на предметном столике исследуемый объект и убедиться, что свет от светодиода освещает нужную область объекта. § Вращением винта 9 добиться появления на экране четкой картины колец Ньютона. Сохранение изображения: § Сфотографировать полученное изображение. § Сохранить фотографию в папке «Студенты, 2курс». Градуировка изображения: § Открыть изображение колец Ньютона в программе Paint (нажать внизу слева Paint) и провести измерения диаметров соответствующих темных колец Ньютона в пикселях (например, диаметры 1-ого и 6–ого кольца). Для этого выбрать “линию”, нажать Shift и с помощью правой копки мыши соединить диаметрально противоположные точки белой линией, записать координаты этих точек. § В программе Paint открыть изображение шкалы микрообъекта, определить, сколько пикселей содержится в 1мкм, и выразить диаметр колец Ньютона в миллиметрах.
|
||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 535; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.46.174 (0.009 с.) |

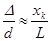 , (14)
, (14)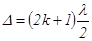 . Используя формулу (14), получим
. Используя формулу (14), получим 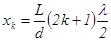 . Аналогично расстояние между нулевым максимумом и минимумом порядка m будет равно
. Аналогично расстояние между нулевым максимумом и минимумом порядка m будет равно 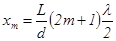 . Откуда расстояние между k-ой и m-ой темными полосами равно
. Откуда расстояние между k-ой и m-ой темными полосами равно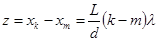
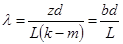 , (15)
, (15)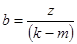 – ширина интерференционной полосы.
– ширина интерференционной полосы.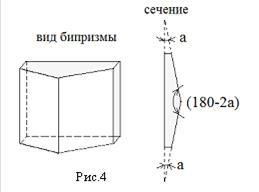 Опыт с бипризмой является одним из наиболее простых в практическом осуществлении опытов по наблюдению интерференции света. Бипризмой называется призма, имеющая два одинаковых острых весьма малых (менее 10) угла a и тупой угол (180о - 2a). Вид бипризмы и ее сечение показаны на рисунке 4. Схема опыта включает в себя источник света, щель, бипризму. Щель освещается источником света и устанавливается строго параллельно ребру тупого угла бипризмы. Световые лучи, проходящие сквозь верхнюю половину бипризмы (за счет преломления на границе "воздух - материал бипризмы"), отклоняются вниз, а лучи, проходящие сквозь нижнюю половину, - вверх. Таким образом, обеспечивается для получения интерференционной картины область перекрытия волн. Когерентными источниками являются мнимые изображения щели S1 и S2, лежащие на пересечении продолжений прошедших сквозь призму лучей (Рис.5).
Опыт с бипризмой является одним из наиболее простых в практическом осуществлении опытов по наблюдению интерференции света. Бипризмой называется призма, имеющая два одинаковых острых весьма малых (менее 10) угла a и тупой угол (180о - 2a). Вид бипризмы и ее сечение показаны на рисунке 4. Схема опыта включает в себя источник света, щель, бипризму. Щель освещается источником света и устанавливается строго параллельно ребру тупого угла бипризмы. Световые лучи, проходящие сквозь верхнюю половину бипризмы (за счет преломления на границе "воздух - материал бипризмы"), отклоняются вниз, а лучи, проходящие сквозь нижнюю половину, - вверх. Таким образом, обеспечивается для получения интерференционной картины область перекрытия волн. Когерентными источниками являются мнимые изображения щели S1 и S2, лежащие на пересечении продолжений прошедших сквозь призму лучей (Рис.5).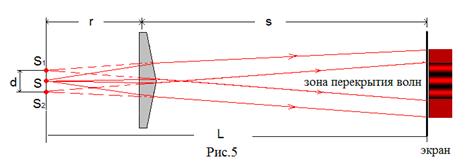
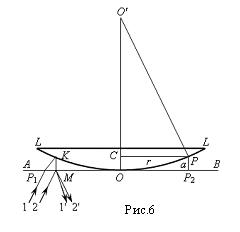 На рис. 6 изображена в вертикальном разрезе плосковыпуклая линза LL, сферической поверхностью соприкасающаяся с плоской поверхностью полированной стеклянной пластины АВ. Между сферической поверхностью линзы и плоской пластинкой имеется воздушный слой, толщина которого увеличивается от точки соприкосновения 0 к краям линзы. В точках P1 и Р2, равноотстоящих от точки 0, толщина слоя одинакова. На всей поверхности пластины равные толщины слоя располагаются по концентрическим окружностям с центром в точке 0. Если осветить систему плоская пластинка-линза параллельным пучком монохроматического света, то в отраженном свете наблюдается большое число чередующихся светлых и темных концентрических колец с темным пятном в области точки 0 (кольца Ньютона). Причем интерференционная картина будет локализована на (или вблизи) отражающей поверхности пластинки. Это связано с тем, что обычно используется небольшой, но протяженный источник света (например, нить накала лампы). Только вблизи поверхности пластинки интерференционные картины от всех точек источника совпадают и, соответственно, усиливают друг друга.
На рис. 6 изображена в вертикальном разрезе плосковыпуклая линза LL, сферической поверхностью соприкасающаяся с плоской поверхностью полированной стеклянной пластины АВ. Между сферической поверхностью линзы и плоской пластинкой имеется воздушный слой, толщина которого увеличивается от точки соприкосновения 0 к краям линзы. В точках P1 и Р2, равноотстоящих от точки 0, толщина слоя одинакова. На всей поверхности пластины равные толщины слоя располагаются по концентрическим окружностям с центром в точке 0. Если осветить систему плоская пластинка-линза параллельным пучком монохроматического света, то в отраженном свете наблюдается большое число чередующихся светлых и темных концентрических колец с темным пятном в области точки 0 (кольца Ньютона). Причем интерференционная картина будет локализована на (или вблизи) отражающей поверхности пластинки. Это связано с тем, что обычно используется небольшой, но протяженный источник света (например, нить накала лампы). Только вблизи поверхности пластинки интерференционные картины от всех точек источника совпадают и, соответственно, усиливают друг друга.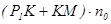 , для воздушного слоя n0=1. Кроме указанной разности хода появляется дополнительная разность хода в полволны (λ/2) вследствие отражения луча 1 в точке К от оптически более плотной среды (стекла линзы). Таким образом, полная оптическая разность хода будет равна:
, для воздушного слоя n0=1. Кроме указанной разности хода появляется дополнительная разность хода в полволны (λ/2) вследствие отражения луча 1 в точке К от оптически более плотной среды (стекла линзы). Таким образом, полная оптическая разность хода будет равна: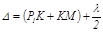
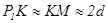 и, соответственно, оптическую разность хода между лучами 1 и 2 представить в виде:
и, соответственно, оптическую разность хода между лучами 1 и 2 представить в виде: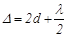 (16)
(16)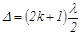 , (17)
, (17)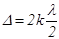 (18)
(18)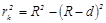 ,
,
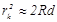 (19)
(19)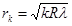 (20)
(20)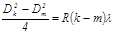 . (21)
. (21)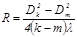 (22)
(22) Опыт Поля. Для демонстрации явления интерференции света большой аудитории наиболее пригоден опыт Поля, который характеризуется большой светосилой и позволяет получить яркую интерференционную картину на стене и потолке. Интерференционная картина образуется вследствие наложения лучей, отраженных от поверхностей тонкой плоскопараллельной пластинки. Роль когерентных источников играют мнимые изображения S1 и S2 источника S (Рис. 7). Этот опыт предъявляет менее жесткие требования к размерам источника S, чем рассмотренные выше опыты.
Опыт Поля. Для демонстрации явления интерференции света большой аудитории наиболее пригоден опыт Поля, который характеризуется большой светосилой и позволяет получить яркую интерференционную картину на стене и потолке. Интерференционная картина образуется вследствие наложения лучей, отраженных от поверхностей тонкой плоскопараллельной пластинки. Роль когерентных источников играют мнимые изображения S1 и S2 источника S (Рис. 7). Этот опыт предъявляет менее жесткие требования к размерам источника S, чем рассмотренные выше опыты.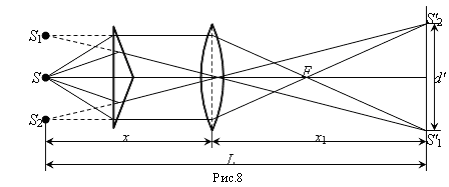
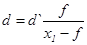 , (23)
, (23)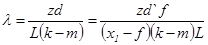 (24)
(24)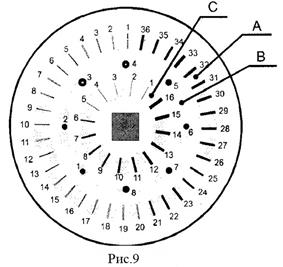 Задание 3. Используя He-Ne–лазер (λ=0.63мкм) и тест-объект МОЛ-01, продемонстрировать интерференцию света от двух щелей (опыт Юнга). Учебный демонстрационный тест-объект МОЛ-01 (Рис.9) представляет собой стеклянную подложку с зеркальным непрозрачным покрытием и с выполненными по специальной фотолитографической технологии прозрачными структурами (одиночные и двойные штрихи, круглые отверстия, кольца и т. д.). Они расположены в трех рядах через равные угловые промежутки. Ряд А – двойные щели с переменными расстоянием между щелями d и шириной щели b. Ряд С – одинарные щели, ряд В- круглые отверстия, отверстия с центральным непрозрачным диском и зонная пластинка с диаметром первой открытой зоны 200мкм и общим числом зон 21. В центре квадратная сетка из прозрачных штрихов шириной 6 мкм и периодами 50 мкм по обеим координатам. Общее число штрихов по каждой координате – 100. Длина каждого штриха -5мм.
Задание 3. Используя He-Ne–лазер (λ=0.63мкм) и тест-объект МОЛ-01, продемонстрировать интерференцию света от двух щелей (опыт Юнга). Учебный демонстрационный тест-объект МОЛ-01 (Рис.9) представляет собой стеклянную подложку с зеркальным непрозрачным покрытием и с выполненными по специальной фотолитографической технологии прозрачными структурами (одиночные и двойные штрихи, круглые отверстия, кольца и т. д.). Они расположены в трех рядах через равные угловые промежутки. Ряд А – двойные щели с переменными расстоянием между щелями d и шириной щели b. Ряд С – одинарные щели, ряд В- круглые отверстия, отверстия с центральным непрозрачным диском и зонная пластинка с диаметром первой открытой зоны 200мкм и общим числом зон 21. В центре квадратная сетка из прозрачных штрихов шириной 6 мкм и периодами 50 мкм по обеим координатам. Общее число штрихов по каждой координате – 100. Длина каждого штриха -5мм.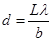 (25)
(25)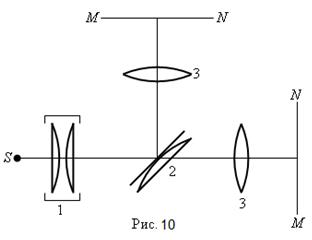 Задание 7. Используя комбинацию плоскопараллельной пластинки и линзы (из школьного набора), продемонстрировать на школьной оптической скамье кольца Ньютона в проходящем и отраженном свете. Оптическая схема установки дана на рис. 10, где S – источник света, I - конденсор, 2 - линза с пластинкой, 3 – объектив от школьной оптической скамьи, MN - экран. При демонстрации можно пользоваться светофильтром, помещая его за объективом. Светофильтр увеличивает временную когерентность излучения и, соответственно, увеличивается по сравнению с белым светом количество наблюдаемых полос интерференции.
Задание 7. Используя комбинацию плоскопараллельной пластинки и линзы (из школьного набора), продемонстрировать на школьной оптической скамье кольца Ньютона в проходящем и отраженном свете. Оптическая схема установки дана на рис. 10, где S – источник света, I - конденсор, 2 - линза с пластинкой, 3 – объектив от школьной оптической скамьи, MN - экран. При демонстрации можно пользоваться светофильтром, помещая его за объективом. Светофильтр увеличивает временную когерентность излучения и, соответственно, увеличивается по сравнению с белым светом количество наблюдаемых полос интерференции.