
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методичні вказівки до виконання лабораторних робіт з курсу фізики оптичного зв’язкуСодержание книги
Поиск на нашем сайте
МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ ЛАБОРАТОРНИХ РОБІТ З КУРСУ ФІЗИКИ ОПТИЧНОГО ЗВ’ЯЗКУ
Київ 2012 Затверджено на засіданні кафедри фізики Державного університету інформаційно-комунікаційних технологій як Методичні вказівки до виконання лабораторних робіт з курсу Фізики оптичного зв’язку (протокол № ___ від _______________р.) Завідувач кафедрою фізики___________Л.М. Гориня
Зміст
Лабораторне заняття №1. Обробка результатів вимірювань при виконанні лабораторних робіт …………....................4 Лабораторне заняття №2. Сферична аберація оптичних лінз …………..……….…………………………………...…...7 Лабораторне заняття №3. Вимірювання довжини хвилі джерела світла за допомогою дифракційної гратки ……….15 Лабораторне заняття №4. Вивчення фотоелектрорушійної сили …………………………………………………….......24 Лабораторне заняття №5. Вивчення фотопровідності речовини ………………………………………………...………28 Лабораторне заняття №6. Вивчення дифракційної ґратки………………………………………………………………..33 Лабораторне заняття №7 Вивчення закону Малюса ………………………………………………………..……………43 Лабораторне заняття №8 Вивчення лінійчатих спектрів випромінювання……………………………………………..53
Лабораторне заняття №1 (вступне) Обробка результатів вимірювань при виконанні лабораторних робіт з курсу «Фізика оптичного зв’язку» Вимірювання фізичних величин є метою кожної лабораторної роботи з фізики. Вимірювання – це процес порівняння фізичної величини з іншою, якає є однорідною з нею, і яка прийнята за одиницю вимірювання. При цьому розрізняють прямі та непрямі вимірювання. Прямими називаються вимірювання, при яких результати отримуються безпосередньо в процесі вимірювання. Непрямими називають вимірювання, в яких значення фізичних величин обчислюють за формулами, які включають в себе фізичні величини, що визначаються при прямих вимірюваннях. Процес вимірювання неможливо здійснити ідеально точно тому, що в результаті отримуються не дійсні (істинні) значення фізичної величини, а наближені (виміряні). Точність вимірювання – це ступінь наближення виміряного значення до істинного. Кількісною мірою такої точності є похибки вимірювання. Абсолютна похибка ( Відносна похибка обчислюється із співвідношення:
і виражається у відсотках. За походженням похибки бувають систематичні – як наслідок несправності приладу, помилковості методу вимірювання та ін., систематична похибка має один і той же знак при кожному вимірюванні і не зменшується при збільшенні кількості вимірювань; випадкові – мимоволі внесені експериментатором внаслідок недосконалості органів чуттів, через обмеженість точності приладу і т.д., випадкова похибка має один і той же знак і зменшується при збільшенні кількості вимірювань. В процесі вимірювання систематичні похибки враховуються або виключаються, випадкові оцінюються шляхом обчислень на основі теорії ймовірності.
Обчислення похибок при прямих вимірюваннях. При проведенні прямих вимірювань спочатку обчислюють середнє арифметичне значення виміряної фізичної величини:
де n – кількість дослідів. Потім обчислюють середню квадратичну похибку за формулою:
де n – кількість дослідів. Наступним кроком є обчислення абсолютної похибки за формулою:
де
Після цього відносна похибка обчислюється за формулою (1), а результат зручно записувати у вигляді:
де після дужок записується розмірність шуканої фізичної величини, а після "=" числове значення відносної похибки. Описаний вище метод обчислення похибок носить назву методу Стьюдента.
Сферична аберація оптичних лінз
Мета роботи. Вивчення основних характеристик і дефектів оптичних лінз.
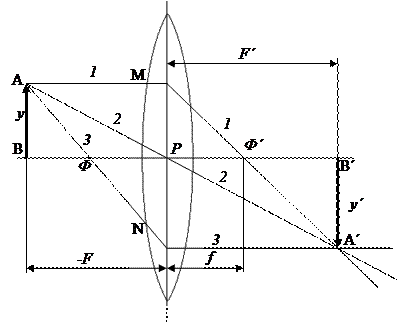
Теоретичні відомості. Лінзою називається прозоре тіло з певним показником заломлення n, обмежене однією або двома сферичними (іноді циліндричними) поверхнями. Лінія, що проходить через центри кривизни поверхонь, називається головною оптичною віссю лінзи. Методи геометричної оптики дозволяють встановити основні оптичні характеристики лінз по відношенню до джерел (предметів), які розташовані поблизу від оптичної осі. Будемо розглядати тонку лінзу, в якої відстань між обмежуючими поверхнями мала в порівнянні з діаметром лінзи. На рис. 1 зображена тонка опукло-вгнута лінза (меніск), у якої радіуси передньої
Рис. 1.
Рис. 2.
Рис. 3 Рис. 4
Промені, що виходять від джерела світла S, що лежить на головній оптичній осі, заломившись на передній поверхні лінзи перетнуться в деякій точці S*, яка розташована на відстані F* від оптичного центра. Величина F* може бути знайдена із співвідношення
Точка S* по відношенню до задньої поверхні лінзи є джерелом (дійсних або уявних) променів, що заломлюються на цій поверхні. Після заломлення ці промені знову перетнуться в деякій точці S, яка є кінцевим зображенням джерела S, яке дає лінза. Позначаючи відстань від до оптичного центру через одержуємо
Віднімаючи почленно рівняння (1) і (2) і виключаючи тим самим величину F*, яка характеризує положення проміжного зображення S*, отримуємо остаточно:
Це рівняння дозволяє знайти відстань до зображення Для лінзи, розташованої в однорідному середовищі (наприклад, у повітрі) n2 = n1 співвідношення (3) спрощується:
Вводячи відносний показник заломлення nвідн = n/n1, можна вивести формулу лінзи до остаточного вигляду:
Величина
називається оптичною силою лінзи, а зворотна їй величина Якщо вимірювати фокусну відстань При Пучок паралельних променів, нахилених до головної оптичної осі під малим кутом α, також збирається в одну точку, яка лежить у площині, що проходить через головний фокус Ф і перпендикулярна до головної оптичної осі (рис. 2). Ця площина називається фокальною площиною. Розглянуті властивості тонких лінз дозволяють геометрично будувати зображення предметів, що являють собою сукупність зображень окремих точок предмета. Якщо предмет лінійний, то при цьому досить побудувати зображення двох його крайніх точок. Для знаходження зображення кожної окремої точки необхідно геометрично побудувати перетинання променів, що виходять із цієї точки, після їхнього заломлення в лінзі. В принципі при цьому досить знайти перетинання будь-яких двох із цих променів. Практично ж, якщо відомі положення оптичного центру і головних фокусів, легко побудувати три промені та проконтролювати себе, перевіряючи, чи перетнуться всі вони в одній точці. Для прикладу на рис. 4 побудовано зображення лінійного предмета АВ, отримане за допомогою збірної лінзи. Із загального пучка променів, що виходять із точки А, виділимо три промені: 1, 2 і 3. Промінь 1 йде паралельно головній оптичній осі та після заломлення проходить через задній фокус Ф'. Промінь 2 проходить через передній головний фокус Ф і після заломлення піде паралельно головній оптичній осі. Нарешті промінь 3, що проходить через оптичний центр лінзи Предмет АВ на рис. 4 розміщений на відстані F, більшій за головну фокусну відстань При виводі основних співвідношень для лінзи передбачалося, що пучок променів, що виходять із кожної світної точки, після заломлення сходиться в певній точці зображення. Таке зображення називається стигматичним. З міркувань також слідує, що це припущення виконується приблизно для вузьких пучків променів, що йдуть поблизу головної оптичної осі (параксіальні промені). Для збільшення світлосили лінзи потрібно збільшувати вхідну зіницю і використовувати промені, що падають під більшими кутами до поверхні, що й приводить до появи спотворень, об'єднаних загальним терміном дефекти лінз. У цій роботі розглядається сферична аберація.
Сферична аберація.
На рис. 5 показаний хід променів від джерела
Рис. 5.
Наявність сферичної аберації робить дещо невизначеним поняття фокуса та фокальної площини лінзи. На екрані, перпендикулярному до оптичної осі, зображення буде не точковим, а матиме вигляд нерівномірно освітленого кола, діаметр якого буде мінімальним не в точці S', а трохи ближче до лінзи. Для зменшення сферичної аберації можна діафрагмувати пучок, обмежуючи його променями, близькими до параксіальних. Однак введення діафрагми знижує світлосилу лінзи. Іншим способом боротьби зі сферичною аберацією є комбінування збірної (
Домашнє завдання. Для виконання роботи необхідно вивчити зазначені нижче питання з курсу фізики: основні закони геометричної оптики; оптична лінза і її властивості; побудова зображень в оптичній лінзі; оптичні системи і їхні похибки.
Лабораторне завдання. 1. Зібрати схему, зазначену на рис. 6. Розмістити досліджувану лінзу на відстані 30 - 50 см від джерела випромінювання. 2. Переміщаючи екран вздовж оптичної лави домогтися максимально чіткого зображення джерела випромінювання на екрані. Виміряйте фокусну відстань. 3. Проведіть 7-10 вимірювань. Результати вимірювань занесіть у таблицю.
4. Визначите середнє значення фокусної відстані для проведеної групи вимірювань
5. Обчисліть середню квадратичну похибку проведених вимірювань за формулою:
6. Обчисліть оптичну силу лінзи за формулою:
Якщо 7. Помістити перед лінзою першу діафрагму, що закриває центральні промені. Домогтися максимального фокусування променів. Повторити вимірювання та обчислення описані в пп. 2-5. 8. Помістити перед лінзою другу діафрагму, що закриває периферійні промені. Повторити вимірювання та обчислення описані в пп. 2-5. 9. Визначити значення сферичної аберації лінзи (різниця середніх значень фокусних відстаней для обох діафрагм) і похибку її визначення (сума середньоквадратичних похибок, обчислених для першої та другої діафрагм). 10. У висновках до роботи вкажіть яке значення сферичної аберації виявлено в збірної оптичної лінзи, яка використовувалась в лабораторній роботі. Прилади та обладнання. У роботі використовуються: оптична лава, джерело світла, збірна лінза, набір діафрагм.
Література. 1. Савельев Н.В. Курс общей физики. М.:Наука. 1978.Т.2, 1979.Т.3. 2. Зисман Г.А., Тодес О.М. Курс общей физики. М.: ГИТТЛ. 1975. 3. Ландсберг Г.С. Оптика М.: ГИТТЛ. 1975. 4. Яворский Б.М., Детлаф А.А. Курс общей физики. М.: Вища школа, 1979. 5. Кортнев А.Б. Практикум по физике. М.: Вища школа. 1967.
Лабораторне заняття № 3
Мета роботи. Дослідити явище дифракції світла та визначити довжину хвилі джерела світла за допомогою дифракційної гратки.
Теоретичні відомості. Дифракція — фізичне явище, пов’язане з непрямолінійним розповсюдженням хвиль, огинанням ними перешкод і проникненням хвилі в область геометричної тіні Дифракцією називаються явища, зумовлені хвильовою природою світла, що спостерігаються при розповсюдженні світла в середовищі з різко вираженими неоднорідностями. Наприклад, у випадках, коли на шляху світла виникають отвори в непрозорих екранах, непрозорі тіла і т.д. Світло – це електромагнітні хвилі з частотами в діапазоні Від частоти світла залежить його колір. Так, наприклад, при Частотний (колірний) склад світла називають спектром, а розділення в просторі цих частот (кольорів, довжин хвиль) називають розкладання світла в спектр. Дифракційною граткою називається перешкода з багатьма щілинами. Одномірна дифракційна гратка являє собою систему, що складається з великого числа однакових по ширині і паралельних одна одній щілин, розділених однаковими по ширині непрозорими проміжками. В роботі використовуються гратка, яка являє собою періодичну послідовність (чергування) щілин шириною b, розділених непрозорими смугами шириною a (рис. 1), розташованих в одній площині. Періодом (постійною) гратки називається величина Загальна картина розповсюдження світла через гратку показана на рис. 2. Гратка опромінюється потоком паралельних променів, перпендикулярних площини гратки. Це відповідає падінню на гратку плоскої хвилі.
Рис. 1. Рис. 2.
За граткою, в ближній області I, розповсюдження світла приблизно відповідає законам геометричної оптики, а дифракція мало помітна. Тут проміння проходить крізь щілини по первинній прямій, за смугами появляються тіні. В проміжній області II дифракція проявляється сильніше, але зберігаються і риси прямолінійного руху падаючих променів. В дальній області III світло розходиться віялоподібно, створюючи неоднорідні потоки світла з чергуванням максимальної і мінімальної інтенсивності світла. Ці максимуми і мінімуми називаються дифракційними. В області III зовсім не зберігається первинний прямолінійний рух променів, що пройшли безперешкодно через щілини. Тут промені відхилились від первинної траєкторії і створили нові світлові потоки. Отже, закони геометричної оптики для розповсюдження світла для цієї області застосувати неможливо, в цій області розповсюдження світла зумовлене хвильовими законами – дифракцією. Кутом дифракції називають кут φ відхилення променя від первинного напрямку. Дифракційним максимумом називають світлові максимуми, викликані дифракцією. Розрахунки показують, що область III з яскраво вираженою дифракцією за перешкодою лежить на відстані В гратці з шириною щілини Якщо відоме місце знаходження фронту хвилі, швидкість хвилі υ в деякий момент часу t, то місце знаходження фронту в наступний момент часу Принцип Гюйгенса є чисто геометричним. Він не вказує способу розрахунку амплітуди хвилі, що огинає вторинні хвилі. Через це принцип Гюйгенса не підходить для розрахунку закономірностей розповсюдження світлових хвиль. Наближений метод вирішення цієї задачі, що є розвитком принципу Гюйгенса, на основі запропонованої Френелем ідеї про когерентність вторинних хвиль та їх інтерференції при накладанні, називається принципом Гюйгенса-Френеля. Цей принцип можна виразити у вигляді ряду положень: • при розрахунку амплітуди світлових коливань, збуджуючих джерелом • вторинні джерела • амплітуда dA коливань, збуджених в точці М вторинних джерел, пропорційна відношенню площі ds відповідної ділянки хвильової поверхні S до відстані r від нього до точки М і залежить від кута α між зовнішньою нормаллю до хвильової поверхні і напрямом від елемента ds до точки М:
де а — величина, пропорційна амплітуді первинної хвилі в точках елемента ds; ƒ(а) монотонно зменшується від 1 при а = 0, до 0 при • якщо частина поверхні S зайнята непрозорими екранами, то відповідні (закриті екранами) вторинні джерела не випромінюють, а інші випромінюють так само, як у відсутність екранів. Падаючу хвилю прийнято називати первинною, а хвилі, які випромінюються точками – вторинними. В точці випромінювання вторинні хвилі мають ту ж частоту і фазу, що і первинна хвиля. Через це вторинні хвилі у вакуумі представляють собою сферичні хвилі, які розходяться з точки випромінювання. Нагадаємо, що промінь представляє собою уявну лінію, вздовж якої розповсюджується хвиля. Промінь перпендикулярний хвильовій поверхні, тому плоска хвиля зображується набором паралельних променів, а сферична – променів, які радіально розходяться із центра сфери. В точці перетину променів відповідні їм хвилі інтерферують (додаються). Нехай в дифракційній гратці є N щілин. Для спрощення кожну щілину гратки представимо однією точкою в просторі. Саме ці і - ті точки будуть випромінювати вторинні хвилі під впливом падаючої хвилі. Зрозуміло, що непрозорі смуги вторинні хвилі не випромінюють. Запишемо напруженість електричного поля вторинної хвилі, що випромінюється і - тою щілиною
де За принципом Гюйгенса-Френеля поле Е в точці спостереження буде представляти собою суму електричного поля вторинної хвилі, випромінюваної і - тою щілиною
Дана сума представляє собою додавання коливань вздовж однієї прямої, через це результуюча хвиля матиме вигляд
Тут На практиці вимірюють і спостерігають не величину напруженості електричного поля хвилі Е(t), а інтенсивність хвилі, яка визначається із співвідношення:
де В загальному випадку аналітичний вираз для (5) з врахуванням (3) має достатньо складний вигляд. Набагато легше отримати вираз для (5), в дальній області, де перетинаються вторинні промені, майже паралельні один одному (на рис. 3 точка М).
Рис. 3. Рис. 4.
За граткою можна поставити збірну лінзу, в результаті чого падаючі на лінзу паралельні вторинні проміння перетнуться у фокальній площині за лінзою (рис. 4). Не вдаючись в математичні деталі, для дифракції в паралельних (вторинних) променях на дифракційних гратках можна отримати наступну залежність інтенсивності І світлової хвилі від кута дифракції φ.
де Кут дифракції φ відраховується від напряму падаючого променя. Цьому куту на відстані L відповідають координати вертикального відхилення Для залежності І(φ) характерним є чергування головних дифракційних максимумів (великих по амплітуді) і побічних дифракційних максимумів (малих по амплітуді). Аналіз виразу (6) дає наступну умову для головних максимумів
де
Рис. 5. Рис. 6.
Дослідження кутів, при яких І = 0, дає кут
Умова головних максимумів пояснюється синфазним додаванням в точці спостереження хвиль від усіх щілин. Дійсно, із рис. 4 видно, що різниця ходу паралельних променів із сусідніх щілин
При різниці фаз Якщо ж в точці спостереження хвилі двох сусідніх щілин протилежні по фазі Більш детальний аналіз виразу (6) показує існування інших максимумів і мінімумів, створюваних додаванням хвиль від великої кількості щілин. Детальніше ці питання викладенні в рекомендованих посібниках. Умова головних максимумів (7) дозволяє визначити довжину хвилі джерела світла
Для цього потрібно навести на дифракційну решітку потік нормально падаючих променів (рис. 4) і на екрані Е, площина якого паралельна площині гратки, отримаємо дифракційну картину. Виміривши відстань
Значення періоду гратки складає
де m – порядок головного максимуму для Якщо падаюче світло складається з набору хвиль різної довжини, то різні хвилі відхиляються на різні кути:
Через це в дифракційних максимумах з
Домашнє завдання. Для виконання роботи необхідно вивчити вказані нижче питання по курсу фізики: Явище дифракції світла. Принцип Гюйгенса – Френеля. Дифракція паралельних променів (дифракція Фраунгофера) на дифракційній гратці.
Прилади та обладнання. 1. Оптична лава. 2. Лазер типу ЛГ-28. 3. Екранна вимірювальна лінійка. 4. Дифракційна гратка.
Література. 1. Савельев И.В. Курс общей физики. Т.2. М.:Наука. 1979. 2. Ландсберг Г.С. Оптика. М.:Наука.. 1976. 3. Зисман ГА. Тодес О.М. Курс общей физики, М.: Наука. 1972. 4 Детлаф А. А. Яворский В. М. Курс физики М Высшая школа 1979
Лабораторне заняття № 4 Мета роботи. Вивчення вентильного фотоефекту в р-п переході.
Теоретичні відомості. Фотоелектрорушійна сила (фотоерс) являє собою різницю потенціалів, що виникає в р-n переході під дією опромінення електромагнітними хвилями. Так званий р-n перехід виникає в перехідній області напівпровідника з різними типами провідності. На рис. 1. зліва від межі поділу розміщено область напівпровідника р - типу, а праворуч показано напівпровідник n - типу.
Виникнення р-n переходу:
Рис. 1.
Різниця концентрації однотипних вільних носіїв електричного заряду в n - і р - областях напівпровідника призводить до дифузії дірок з р - області в n - область і дифузії електронів у протилежному напрямку. Внаслідок цього на межі р - і n - області виникає контактна різниця потенціалів: електрони, що вийшли з n - області, залишають в цій області нескомпенсований позитивний заряд, а дірки, що вийшли з р - області неврівноважений негативний заряд. Дифузія змінює концентрацію носіїв до тих пір, доки не встановиться динамічна рівновага: потік носіїв внаслідок дифузії врівноважується потоком носіїв у зворотному напрямку під дією різниці потенціалів, що виникла на межі р-n переходу. При опроміненні переходу в р - області виникають додаткові електронно-діркові пари. Вільні електрони з цих пар дифундують до р-n переходу і під дією контактного поля переводяться в n - область. Однак дірки подолати потенціальний бар’єр не в змозі і залишаються в р - області. Тому р- область заряд
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.41.109 (0.016 с.) |

 ) вимірювання виражається у тих же одиницях, що і фізична величина, для якої ця похибка обчислюється. Вона задає інтервал (
) вимірювання виражається у тих же одиницях, що і фізична величина, для якої ця похибка обчислюється. Вона задає інтервал ( ), в якому знаходиться істинне значення фізичної величини.
), в якому знаходиться істинне значення фізичної величини. (1)
(1) , (2)
, (2) , (3)
, (3) , (4)
, (4) - коефіцієнт Стьюдента, який береться з таблиці при відомій кількості дослідів n, та надійності p, яку при усіх вимірюваннях в даних лабораторних роботах потрібно брати 0,95:
- коефіцієнт Стьюдента, який береться з таблиці при відомій кількості дослідів n, та надійності p, яку при усіх вимірюваннях в даних лабораторних роботах потрібно брати 0,95: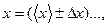 при
при 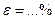 , (5)
, (5) та задньої
та задньої 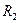 поверхонь позитивні. Розрахунок будемо вести в загальному виді, який застосовний для лінз будь-якої форми (двоопуклої, плоско-вгнутої і т.д.). Оскільки лінза тонка, то відлік відстаней до предмета
поверхонь позитивні. Розрахунок будемо вести в загальному виді, який застосовний для лінз будь-якої форми (двоопуклої, плоско-вгнутої і т.д.). Оскільки лінза тонка, то відлік відстаней до предмета 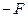 і до зображення
і до зображення  можна вести практично від однієї точки P – оптичного центра лінзи. Показники заломлення середовищ, розташованих попереду і позаду лінзи, позначимо відповідно через n1 і n2.
можна вести практично від однієї точки P – оптичного центра лінзи. Показники заломлення середовищ, розташованих попереду і позаду лінзи, позначимо відповідно через n1 і n2.


 (1)
(1) (2)
(2) (3)
(3) , якщо відома відстань до предмета
, якщо відома відстань до предмета  . (4)
. (4) . (5)
. (5)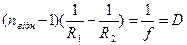 (6)
(6) - головною фокусною відстанню. Пучок паралельних променів, які йдуть від нескінченно віддаленого джерела
- головною фокусною відстанню. Пучок паралельних променів, які йдуть від нескінченно віддаленого джерела  , сходиться в так званому задньому фокусі на відстані F1 = f від її оптичного центра. Промені, що виходять із передньогофокусалінзи F = —
, сходиться в так званому задньому фокусі на відстані F1 = f від її оптичного центра. Промені, що виходять із передньогофокусалінзи F = —  .
. головна фокусна відстань
головна фокусна відстань 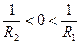 зображений на рис. 2. При
зображений на рис. 2. При  наведений на рис. 3.
наведений на рис. 3.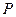 , проходить зовсім не заломлюючись. Перетин цих трьох променів дає точку
, проходить зовсім не заломлюючись. Перетин цих трьох променів дає точку  , яка є зображенням краю А предмета. Опускаючи з
, яка є зображенням краю А предмета. Опускаючи з  , яка є зображенням другого краю предмета В.
, яка є зображенням другого краю предмета В.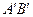 збільшене та перевернуте. Так як точки зображення є перетинами самих променів, а не їхнім продовженням, то таке зображення буде дійсним.
збільшене та перевернуте. Так як точки зображення є перетинами самих променів, а не їхнім продовженням, то таке зображення буде дійсним. , розташованого на оптичній осі, що заломлюються в збірній лінзі великої світлосили. Параксіальні промені перетинаються в точці, що перебуває на відстані
, розташованого на оптичній осі, що заломлюються в збірній лінзі великої світлосили. Параксіальні промені перетинаються в точці, що перебуває на відстані  від оптичного центра лінзи. Чим далі від оптичної осі поширюватиметься вихідний промінь, тим сильніше він буде відхилятися, перетинаючись у все більш близьких до оптичного центра лінзи точках. Самі крайні промені перетнуться в точці
від оптичного центра лінзи. Чим далі від оптичної осі поширюватиметься вихідний промінь, тим сильніше він буде відхилятися, перетинаючись у все більш близьких до оптичного центра лінзи точках. Самі крайні промені перетнуться в точці  , і зображенням світної точки
, і зображенням світної точки  є мірою сферичної аберації. Для збірної лінзи,
є мірою сферичної аберації. Для збірної лінзи, 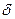 <0, а для розсівної
<0, а для розсівної 
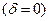 .
. (7)
(7) (8)
(8) (9)
(9) та
та  виміряються в метрах, то
виміряються в метрах, то  виміряється в діоптріях.
виміряється в діоптріях. . Оскільки у вакуумі швидкість світла
. Оскільки у вакуумі швидкість світла  однакова для всіх частот, то довжина хвилі у вакуумі лежить в діапазоні
однакова для всіх частот, то довжина хвилі у вакуумі лежить в діапазоні 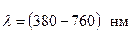 . Відзначимо, що
. Відзначимо, що 
 світлова хвиля, яка сприймається оком, здається червоного кольору. З іншої сторони хвиля з частотою
світлова хвиля, яка сприймається оком, здається червоного кольору. З іншої сторони хвиля з частотою  здається фіолетовою.
здається фіолетовою. , рівна відстані між центральними лініями О1 і О2 сусідніх щілин. Непрозорі щілини настільки вузькі, що неозброєним оком їх практично не видно.
, рівна відстані між центральними лініями О1 і О2 сусідніх щілин. Непрозорі щілини настільки вузькі, що неозброєним оком їх практично не видно.
 , де D – поперечний розмір перешкоди в світловому потоці.
, де D – поперечний розмір перешкоди в світловому потоці. м при довжині хвилі λ=500 нм дифракція від щілини очевидно помітна на відстанях, які більші за 0,2 м. Цей приклад показує, що для спостереження дифракції важливе співвідношення розміру перешкоди і довжини хвилі. Щоб спостерігати дифракцію світлових хвиль поблизу гратки, потрібно вибирати гратки з малим періодом d.
м при довжині хвилі λ=500 нм дифракція від щілини очевидно помітна на відстанях, які більші за 0,2 м. Цей приклад показує, що для спостереження дифракції важливе співвідношення розміру перешкоди і довжини хвилі. Щоб спостерігати дифракцію світлових хвиль поблизу гратки, потрібно вибирати гратки з малим періодом d. можна визначити на основі принципу Гюйгенса. Згідно цього принципу всі точки поверхні
можна визначити на основі принципу Гюйгенса. Згідно цього принципу всі точки поверхні  , через які проходить фронт хвилі у момент часу t, потрібно розглядати як джерела вторинних хвиль, а шукане положення
, через які проходить фронт хвилі у момент часу t, потрібно розглядати як джерела вторинних хвиль, а шукане положення  фронту в момент часу
фронту в момент часу  в довільній точці М, джерело
в довільній точці М, джерело  , (1)
, (1) . Вторинні джерела не випромінюють назад.
. Вторинні джерела не випромінюють назад. (2)
(2) - миттєве значення напруженості поля в точці спостереження М в момент часу t,
- миттєве значення напруженості поля в точці спостереження М в момент часу t,  - амплітуда напруженості поля в точці спостереження, ω – циклічна частота,
- амплітуда напруженості поля в точці спостереження, ω – циклічна частота,  - хвильове число, ri – відстань від і - ої щілини до точки спостереження, αі – початкова фаза коливань. Якщо первинна хвиля падає перпендикулярно до поверхні дифракційної гратки, то коливання хвильового фронту в щілинах синфазні,
- хвильове число, ri – відстань від і - ої щілини до точки спостереження, αі – початкова фаза коливань. Якщо первинна хвиля падає перпендикулярно до поверхні дифракційної гратки, то коливання хвильового фронту в щілинах синфазні,  .
. . (3)
. (3) . (4)
. (4) – амплітуда в точці спостереження,
– амплітуда в точці спостереження,  – відстань до центра гратки О,
– відстань до центра гратки О,  – початкова фаза коливань.
– початкова фаза коливань. (5)
(5) - магнітна постійна, а
- магнітна постійна, а  - електрична постійна.
- електрична постійна.
 , (6)
, (6) - значення інтенсивності світла при φ=0. Графік цієї залежності показаний на рис. 5.
- значення інтенсивності світла при φ=0. Графік цієї залежності показаний на рис. 5. . Картину дифракції можна спостерігати на екрані Е, площина якого паралельна площині гратки.
. Картину дифракції можна спостерігати на екрані Е, площина якого паралельна площині гратки.
 (7)
(7) - кут дифракції m – го максимуму, m – число, яке називається порядком головного максимуму.
- кут дифракції m – го максимуму, m – число, яке називається порядком головного максимуму.
 між сусідніми нулями І(φ). Ця величина
між сусідніми нулями І(φ). Ця величина  . (8)
. (8) . Це викликає різницю фаз в точці перетину променів
. Це викликає різницю фаз в точці перетину променів (9)
(9) коливання синфазні і при додаванні дають найбільшу амплітуду. Іншими словами це наступає при
коливання синфазні і при додаванні дають найбільшу амплітуду. Іншими словами це наступає при  . Після скорочення на 2π отримаємо умову головних максимумів (7).
. Після скорочення на 2π отримаємо умову головних максимумів (7). , то при додаванні такі хвилі гасять одна одну, створюючи нульову інтенсивність, тобто дифракційний мінімум.
, то при додаванні такі хвилі гасять одна одну, створюючи нульову інтенсивність, тобто дифракційний мінімум. (10)
(10) між центральним (m = 0) і m – тим головним максимумом і відстань L між екраном і граткою, отримаємо
між центральним (m = 0) і m – тим головним максимумом і відстань L між екраном і граткою, отримаємо

 (11)
(11) . За відомим значенням d і виміряним значенням L і
. За відомим значенням d і виміряним значенням L і  (12)
(12) .
. (13)
(13) падаюче світло розкладається в спектр.
падаюче світло розкладається в спектр.



