
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обчислення похибок при непрямих вимірюваннях.Содержание книги Поиск на нашем сайте
Досить часто при експериментальних дослідженнях шукають фізичну величину не прямим шляхом, а опосередковано – через вимірювання інших величин. При цьому шукана фізична величина є функцією останніх:
Знаючи явний вигляд рівняння (6) для конкретної лабораторної роботи, потрібно вивести формулу для відносної похибки непрямого вимірювання (у випадку добутку величин (
де Після цього обчислюється абсолютна похибка шуканої фізичної величини:
Кінцевий результат записують аналогічно до попереднього методу обчислення похибок у вигляді:
Лабораторне заняття № 2 Сферична аберація оптичних лінз
Мета роботи. Вивчення основних характеристик і дефектів оптичних лінз.
Теоретичні відомості. Лінзою називається прозоре тіло з певним показником заломлення n, обмежене однією або двома сферичними (іноді циліндричними) поверхнями. Лінія, що проходить через центри кривизни поверхонь, називається головною оптичною віссю лінзи. Методи геометричної оптики дозволяють встановити основні оптичні характеристики лінз по відношенню до джерел (предметів), які розташовані поблизу від оптичної осі. Будемо розглядати тонку лінзу, в якої відстань між обмежуючими поверхнями мала в порівнянні з діаметром лінзи. На рис. 1 зображена тонка опукло-вгнута лінза (меніск), у якої радіуси передньої
Рис. 1.
Рис. 2.
Рис. 3 Рис. 4
Промені, що виходять від джерела світла S, що лежить на головній оптичній осі, заломившись на передній поверхні лінзи перетнуться в деякій точці S*, яка розташована на відстані F* від оптичного центра. Величина F* може бути знайдена із співвідношення
Точка S* по відношенню до задньої поверхні лінзи є джерелом (дійсних або уявних) променів, що заломлюються на цій поверхні. Після заломлення ці промені знову перетнуться в деякій точці S, яка є кінцевим зображенням джерела S, яке дає лінза. Позначаючи відстань від до оптичного центру через одержуємо
Віднімаючи почленно рівняння (1) і (2) і виключаючи тим самим величину F*, яка характеризує положення проміжного зображення S*, отримуємо остаточно:
Це рівняння дозволяє знайти відстань до зображення Для лінзи, розташованої в однорідному середовищі (наприклад, у повітрі) n2 = n1 співвідношення (3) спрощується:
Вводячи відносний показник заломлення nвідн = n/n1, можна вивести формулу лінзи до остаточного вигляду:
Величина
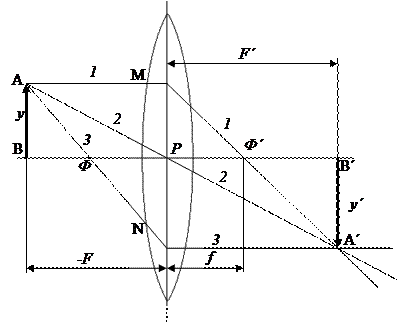
називається оптичною силою лінзи, а зворотна їй величина Якщо вимірювати фокусну відстань При Пучок паралельних променів, нахилених до головної оптичної осі під малим кутом α, також збирається в одну точку, яка лежить у площині, що проходить через головний фокус Ф і перпендикулярна до головної оптичної осі (рис. 2). Ця площина називається фокальною площиною. Розглянуті властивості тонких лінз дозволяють геометрично будувати зображення предметів, що являють собою сукупність зображень окремих точок предмета. Якщо предмет лінійний, то при цьому досить побудувати зображення двох його крайніх точок. Для знаходження зображення кожної окремої точки необхідно геометрично побудувати перетинання променів, що виходять із цієї точки, після їхнього заломлення в лінзі. В принципі при цьому досить знайти перетинання будь-яких двох із цих променів. Практично ж, якщо відомі положення оптичного центру і головних фокусів, легко побудувати три промені та проконтролювати себе, перевіряючи, чи перетнуться всі вони в одній точці. Для прикладу на рис. 4 побудовано зображення лінійного предмета АВ, отримане за допомогою збірної лінзи. Із загального пучка променів, що виходять із точки А, виділимо три промені: 1, 2 і 3. Промінь 1 йде паралельно головній оптичній осі та після заломлення проходить через задній фокус Ф'. Промінь 2 проходить через передній головний фокус Ф і після заломлення піде паралельно головній оптичній осі. Нарешті промінь 3, що проходить через оптичний центр лінзи Предмет АВ на рис. 4 розміщений на відстані F, більшій за головну фокусну відстань При виводі основних співвідношень для лінзи передбачалося, що пучок променів, що виходять із кожної світної точки, після заломлення сходиться в певній точці зображення. Таке зображення називається стигматичним. З міркувань також слідує, що це припущення виконується приблизно для вузьких пучків променів, що йдуть поблизу головної оптичної осі (параксіальні промені). Для збільшення світлосили лінзи потрібно збільшувати вхідну зіницю і використовувати промені, що падають під більшими кутами до поверхні, що й приводить до появи спотворень, об'єднаних загальним терміном дефекти лінз. У цій роботі розглядається сферична аберація.
Сферична аберація.
На рис. 5 показаний хід променів від джерела
Рис. 5.
Наявність сферичної аберації робить дещо невизначеним поняття фокуса та фокальної площини лінзи. На екрані, перпендикулярному до оптичної осі, зображення буде не точковим, а матиме вигляд нерівномірно освітленого кола, діаметр якого буде мінімальним не в точці S', а трохи ближче до лінзи. Для зменшення сферичної аберації можна діафрагмувати пучок, обмежуючи його променями, близькими до параксіальних. Однак введення діафрагми знижує світлосилу лінзи. Іншим способом боротьби зі сферичною аберацією є комбінування збірної (
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 264; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.160.29 (0.007 с.) |

 , (6)
, (6) ):
): , (7)
, (7) – абсолютні похибки вимірювання фізичних величин
– абсолютні похибки вимірювання фізичних величин 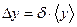 (8)
(8) при
при 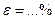 , (9)
, (9) та задньої
та задньої 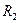 поверхонь позитивні. Розрахунок будемо вести в загальному виді, який застосовний для лінз будь-якої форми (двоопуклої, плоско-вгнутої і т.д.). Оскільки лінза тонка, то відлік відстаней до предмета
поверхонь позитивні. Розрахунок будемо вести в загальному виді, який застосовний для лінз будь-якої форми (двоопуклої, плоско-вгнутої і т.д.). Оскільки лінза тонка, то відлік відстаней до предмета 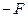 і до зображення
і до зображення  можна вести практично від однієї точки P – оптичного центра лінзи. Показники заломлення середовищ, розташованих попереду і позаду лінзи, позначимо відповідно через n1 і n2.
можна вести практично від однієї точки P – оптичного центра лінзи. Показники заломлення середовищ, розташованих попереду і позаду лінзи, позначимо відповідно через n1 і n2.


 (1)
(1) (2)
(2) (3)
(3) , якщо відома відстань до предмета
, якщо відома відстань до предмета  . (4)
. (4) . (5)
. (5)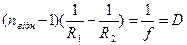 (6)
(6) - головною фокусною відстанню. Пучок паралельних променів, які йдуть від нескінченно віддаленого джерела
- головною фокусною відстанню. Пучок паралельних променів, які йдуть від нескінченно віддаленого джерела  , сходиться в так званому задньому фокусі на відстані F1 = f від її оптичного центра. Промені, що виходять із передньогофокусалінзи F = —
, сходиться в так званому задньому фокусі на відстані F1 = f від її оптичного центра. Промені, що виходять із передньогофокусалінзи F = —  .
. головна фокусна відстань
головна фокусна відстань 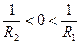 зображений на рис. 2. При
зображений на рис. 2. При  наведений на рис. 3.
наведений на рис. 3.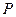 , проходить зовсім не заломлюючись. Перетин цих трьох променів дає точку
, проходить зовсім не заломлюючись. Перетин цих трьох променів дає точку  , яка є зображенням краю А предмета. Опускаючи з
, яка є зображенням краю А предмета. Опускаючи з  , яка є зображенням другого краю предмета В.
, яка є зображенням другого краю предмета В.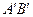 збільшене та перевернуте. Так як точки зображення є перетинами самих променів, а не їхнім продовженням, то таке зображення буде дійсним.
збільшене та перевернуте. Так як точки зображення є перетинами самих променів, а не їхнім продовженням, то таке зображення буде дійсним. , розташованого на оптичній осі, що заломлюються в збірній лінзі великої світлосили. Параксіальні промені перетинаються в точці, що перебуває на відстані
, розташованого на оптичній осі, що заломлюються в збірній лінзі великої світлосили. Параксіальні промені перетинаються в точці, що перебуває на відстані  від оптичного центра лінзи. Чим далі від оптичної осі поширюватиметься вихідний промінь, тим сильніше він буде відхилятися, перетинаючись у все більш близьких до оптичного центра лінзи точках. Самі крайні промені перетнуться в точці
від оптичного центра лінзи. Чим далі від оптичної осі поширюватиметься вихідний промінь, тим сильніше він буде відхилятися, перетинаючись у все більш близьких до оптичного центра лінзи точках. Самі крайні промені перетнуться в точці  , і зображенням світної точки
, і зображенням світної точки  є мірою сферичної аберації. Для збірної лінзи,
є мірою сферичної аберації. Для збірної лінзи, 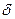 <0, а для розсівної
<0, а для розсівної 
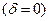 .
.


