Методы решения задач оптимизации в АСУ

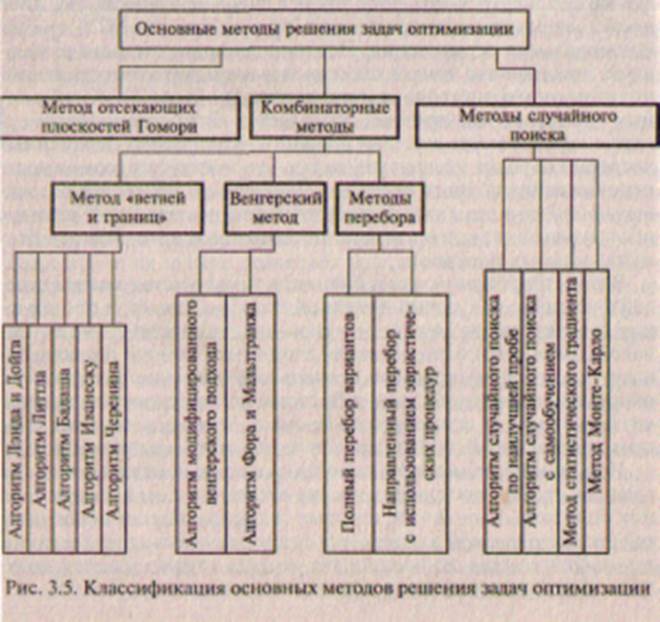
Математическое обеспечение позволяет использовать методы ав­томатизированного поиска оптимальных вариантов при проекти­ровании системы.

Часто при решении задач оптимизации одновременно использу­ются несколько критериев (многокритериальность). Оптимизация параметров за счет выделения одной из критериальных функций в ранг целевой не всегда приносит желаемые результаты. В этом слу­чае можно использовать либо процедурную декомпозицию, либо последовательно совершенствовать проектируемую АСУ, сменяя критериальные ограничения. Неоднородность и высокая размер­ность пространства поиска также вызывают необходимость декомпозиционного подхода к проектированию АСУ. К указан­ным факторам, как правило, добавляется дискретность перемен­ных и нелинейность целевой функции. Количество переменных достигает порядка нескольких тысяч, что исключает возможность использования полного перебора. Неприемлем также подход, зак­лючающийся в решении соответствующей непрерывной задачи с последующим округлением нецелоисчисленных компонент до бли­жайших целых значений.

В качестве решения может быть использован метод замены целе­вой функции с ее кусочно-линейной аппросимакцией и последую­щее решение задачи методом отсекающих плоскостей Гомори. Од­нако возможности использования алгоритмов Гомори ограничива­ются тем, что формирование правильного отсечения сопряжено с определенными трудностями и быстрым ростом размерности зада­чи за счет новых ограничений. Кроме того, полученное решение представляет собой лишь аппроксимацию оптимального решения.

Использование методов, основанных на идее метода «ветвей и границ», требует построения правил ветвления и вычисления оце­нок получаемых множеств, которые сильно зависят от особеннос­тей рассматриваемой задачи. Хотя эти методы весьма эффективны в вычислительном отношении, не во всех случаях удается полу­чить эффективные правила ветвления и вычисления оценок.

Наибольшее распространение при решении задач с большим числом переменных получили приближенные методы и, в первую очередь, методы направленного поиска с использованием деком­позиции и разнообразных эвристических приемов. Вместе с тем можно считать целесообразным поиск новых эвристических про­цедур, существенно сокращающих число возможных вариантов перебора и упрощающих процесс оценки получаемых вариантов. Очевидно, что такие процедуры должны основываться на физи­ческом смысле задачи и ее особенностях (рис. 3.5).

Большая размерность и высокая сложность задач, решаемых на этапе системного программирования, дискретность переменных, не разработанность соответствующих математических моделей и ме­тодов, а также сложность получения выражения целевой функции определяют необходимость разработки новых методов и алгорит­мов.

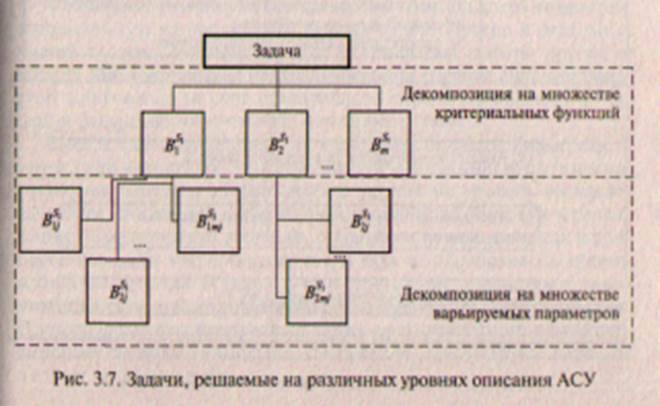
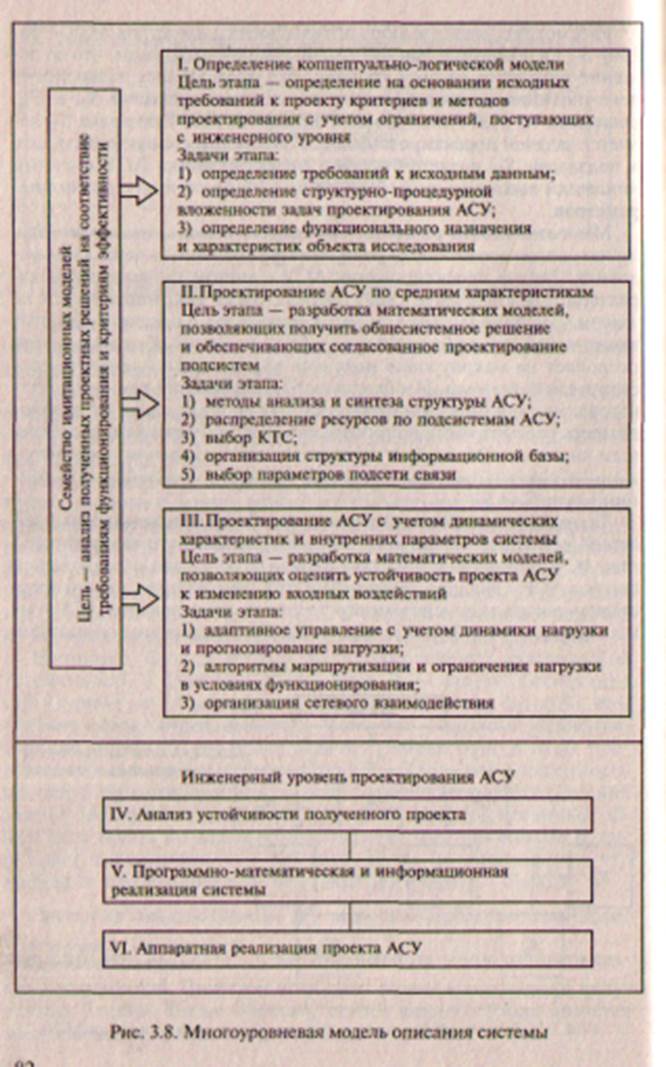
Анализ показывает, что единственно возможным в данном слу­чае является декомпозиционный подход к решению задач этапа системного проектирования. Основная идея декомпозиционного подхода состоит в последовательной оптимизации по одному из управляемых параметров при ограничениях на остальные управляемые параметры. Использование декомпозиционного подхода к проектированию АСУ позволяет существенно упростить задачу проектировщиков. При таком подходе задачи проектирования под­сети связи и полсети вычислительных ресурсов и пользователей решаются в соответствии с принципом покомпонентного спуска, обеспечивающим поочередное решение частных задач и установления связи между ними. При этом полученное решение является субоптимальным. Сложность получения точного решения опреде­ляется, с одной стороны, недостаточностью задания исходных данных и, с другой стороны, следует из того факта, что для реше­ния общей задачи проектирования используется се декомпозиция па подзадачи. При этом оптимизация каждой подзадачи S_i, i = 1,…, I из множества всех подзадач приводит к субоптимальным решениям задачи S *, составленной из всех этих подзадач.

Если при решении частных задач принципиально возможно ис­пользование универсальных математических методов, то разработка процедур координации необходима при проектировании каждой кон­кретной системы. Именно поэтому вопросы координации решений, получаемых при проектировании каждой из подсистем АСУ, наибо­лее сложны и в настоящее время проработаны недостаточно полно.

Попытка синтеза АСУ сразу по всем параметрам с учетом всех ограничителей нереальна как по объему информации, так и по трудоемкости вычислительных работ. Методология синтеза АСУ представляет собой разбиение общих задач проектирования па ряд взаимосвязанных подзадач, установление информационного обмена и последовательности их выполнения.

Основная трудность заключается в нахождении компромисса между простотой описания и необходимостью учета многочисленных характеристик АСУ. Решение этой проблемы заключается в иерархическом описании, при котором система представляется семейством моделей, каждая из которых описывает поведение системы на различных уровнях абстракции. Для эффективности такого описания системы необходима наибольшая независимость моделей для различных уровней. Рассмотренные выше обстоя­тельства приводят к схеме структурно-процедурной вложенности задач проектирования АСУ (рис. 3.6).

В задаче верхнего уровня 5, при заданных требованиях к функ­ционированию следует определить общие принципы построения АСУ, которые в дальнейшем позволяют сформулировать матема­тическую модель АСУ. В задаче второго уровня в условиях извест­ных входных воздействий и общих принципов функционирования требуется синтезировать оптимальные параметры АСУ. В задаче третьего уровня требуется проанализировать выбранные парамет­ры АСУ на соответствие заданным критериям, используя метод имитационного моделирования.

Понятие вложенности процессов проектирования в данном слу­чае отражает строгую последовательность решения задач и степень конкретизации принимаемых решений.

После подобной неформальной декомпозиции проблема деком­позиции не снимается, а подчиняется новым требованиям обес­печения автоматизированного поиска решений с использованием формальных процедур.

Рассмотрим более подробно задачу S₁. Наличие нескольких кри­териев, которые в данном случае невозможно свести к одному фун­кциональному критерию, и неоднородность пространства варьиру­емых параметров обусловливают дальнейшую декомпозицию, реализуемую на принципах однородности критериальных функ­ций и пространства поиска. Над задачей S₁, проводится формаль­ная декомпозиция на

B _р, р = 1,…, m блоков, в функции каждого из которых входит расчет одной из критериальных функций.

Например, блок B ₁ решает задачу обеспечения классической устойчивости и адаптируемости, блок В₂ — задачу обеспечения структурной устойчивости и надежности. Целевая функция все­гда выносится в отдельный блок. Часто это — экономические тре­бования. При этом все блоки задачи 5, имеют одно и то же про­странство варьируемых параметров R _х. Здесь нет вложенности процедур проектирования, так как последовательность решения задач в блоках не является существенной. Информационный об­мен типа «связь по варьируемым параметрам» для блоков B _р по­рождает дополнительные обратные связи по управлению, что приводит к необходимости многократного синтеза блоков.

Далее над каждым блоком В_р^S1 возможно провести декомпози­цию на блоки В_{р q} ^{S 1}, q = 1,…, qm, локальные по множеству варьиру­емых параметров. При этом возникает задача координации полу­ченных блоков. Таким образом, синтез каждого блока является многошаговым процессом (рис. 3.7).

        Рассмотрим задачу выбора оптимальных параметров АСУ — задачу S₂. Особенность данной задачи заключается в том, что ее решение находится на двух уровнях. Это представляет дальнейшую декомпозицию задачи S₂на две вложенные подзадачи S₂₁ и S₂₂, решаемые на различных уровнях описания АСУ. Подзадача S₂₁ является задачей проектирования АСУ по средним характеристикам, а по палача S₂₂ является задачей проектирования АСУ с учетом динамики выходных информационных потоков и внутренних параметров.

Многозначность решений определяет использование метода, заключающегося в поиске решений при различных начальных условиях. Задача проектирования АСУ с учетом динамических характеристик системы в свою очередь также декомпозируется на задачи. Решение указанного множества задач в соответствии с их вложенностью и с обязательным учетом внешних обратных связей   позволяет на макроуровне получить рациональный вариант проектируемой системы. Необходимость координации решений част­ных задач и организации итерационных процедур диктует необходимость рассмотрения вопросов организации управления системным анализом. Объектами управления при системном проектировании являются процедуры первого и второго уровней декомпозиции задач S₁ и S₂.

Таким образом, более детальная разработка изложенных направлений исследования методов автоматизированного проектирования АСУ позволит вплотную подойти к решению общей задачи синтеза АСУ. Обобщая результаты настоящего раздела, можно представить состав задач системного уровня проектирования АСУ и их взаимосвязь (рис. 3.8). Все задачи S_1, S_2, S₃ охвачены обратными связями, обеспечивающими координацию результатов их решений и итерационность процесса проектирования.

Необходимость создания средств автоматизации проектирования таких больших систем, как АСУ, обусловливает интерес проектировщиков к созданию достаточно универсальных и высокопроизводительных методов решения подзадач, указанных на  рис. 3.8.