
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множества в многомерных пространствахСтр 1 из 9Следующая ⇒
Бронштейн Е.М. И00 Функции нескольких переменных: учебное пособие / Е.М.Бронштейн;Уфимск. гос. авиац. техн. ун-т. – Уфа: РИК УГАТУ, 2020. – 86 с. ISBN
Кратко изложено ….……., рассмотрены …………. Предназначено для … Не дублировать гриф с титульного листа (аннотация не должна превышать 600 знаков)
УДК ББК
ISBN © Корректура и верстка. РИК УГАТУ, 2020
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ.. 4 1. МНОЖЕСТВА В МНОГОМЕРНЫХ ПРОСТРАНСТВАХ.. 5 2. ПОСЛЕДОВАТЕЛЬНОСТИ ТОЧЕК В МНОГОМЕРНЫХ ПРОСТРАНСТВАХ 9 3. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ, ПРЕДЕЛ.. 11 4. НЕПРЕРЫВНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.. 16 5. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИРУЕМОСТЬ. 20 6. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ.. 26 7. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНЫХ ОТОБРАЖЕНИЙ.. 31 8. ДИФФЕРЕНЦИАЛ.. 37 9. ПРОИЗВОДНЫЕ ПО НАПРАВЛЕНИЮ... 39 10. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ.. 41 11. ФОРМУЛА ТЕЙЛОРА.. 49 12. ЭКСТРЕМУМЫ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.. 50 13. НЕЯВНЫЕ ФУНКЦИИ.. 59 14. НЕЯВНЫЕ ОТОБРАЖЕНИЯ.. 67 15. УСЛОВНЫЙ ЭКСТРЕМУМ... 72 16. ВЫПУКЛОСТЬ. 75 ЗАКЛЮЧЕНИЕ.. 84 БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 85
ВВЕДЕНИЕ
Раздел математического анализа «Функции нескольких переменных» играет важнейшую роль в ряде математических дисциплин, в частности, теории дифференциальных уравнений математической физики. Уже из названия просматривается прикладное значение этой дисциплины - на ее языке описываются многообразные явления материального мира. Математический анализ является наукой в некотором смысле парадоксальной. С одной стороны это лавка редкостей: в некотором точном смысле непрерывные функции это ничтожно малая часть множества всех функций, а дифференцируемые - ничтожно малая часть множества непрерывных функций. С другой стороны, математический анализ наука преимущественно локальная: исследуется поведение функции в окрестности точки (иногда говорят «сколь угодно малой»). В этом смысле специалисты по математическому анализу сродни ювелирам. При этом, аналитики умеют из малого склеивать и большое. В тексте указания на локальную природу объектов выделены полужирным шрифтом.
Изучение этого раздела обычно вызывает затруднения. В нем сочетаются глубокие теоретические построения и основанная на них весьма изысканная техника. Пособие рассчитано на студентов технических направлений и специальностей с углубленной математической подготовкой, в частности, 02.03.03 Математическое обеспечение и администрирование информационных систем. Отметим, что изложение в большей степени, чем обычно, опирается на конструкции линейной алгебры. Добавлены разделы (неявные отображения, выпуклые функции), которые, как правило, не включаются в курс и рассчитаны на заинтересованных студентов. Следуя традиции функционального анализа, разделяются функции (одномерные) и отображения (многомерные). Все разделы сопровождаются вопросами для самопроверки и упражнениями, которые, конечно, не заменяют задачника.
ДИФФЕРЕНЦИАЛ По определению 11 функция n переменных f (M) называется дифференцируемой в точке M 0, если ее приращение D f (M 0) представимо в виде Определение 13. Дифференциалом называется линейная функция от (D x 1,...,D x n) вида
Таким образом, из приращения выделена линейная часть. Говорят о «главной линейной части приращения» в том смысле, что отброшена бесконечно малая более высокого порядка. Такая терминология неприменима при нулевом дифференциале. В силу независимости приращений переменных для каждого аргумента xi (производные от xi по другим переменным равны 0) справедливо равенство Геометрический смысл дифференциала функции двух переменных аналогичен смыслу дифференциала функции одной переменной: он равен приращению касательной плоскости к графику функции в точке M 0 при изменении аргументов на d x 1 и d x 2.
Следующее свойство дифференциала является принципиально важным, в частности, при вычислении интегралов. Теорема 12. Форма дифференциала инвариантна, т.е. формула имеет тот же вид, если переменные x 1,..., x n являются функции от каких-либо переменных. Доказательство. Рассмотрим два частных случая, в общем случае выкладки принципиально те же самые. 1. (x, y)®(u, v)® z, считаем, что x, y независимые переменные.
2. Отдельно рассмотрим случай суперпозиции x ®(u, v)® z, поскольку у функций одной переменной есть специфика.
Это свойство позволяет на новом уровне получить известные для функций одной переменной формулы для дифференциалов d (u ± v)= du ± dv, d (uv)= du × v + dv u, d (u/v)=(du × v - dv u)/ v 2. Докажем, например, третью формулу.
Как и для функций одной переменной, дифференциал можно использовать для приближенных вычислений (говорят, в первом приближении). Принимаем, что D f (M 0)» df (M 0). Пример. Вычислить в первом приближении величину 1,022,03. Для этого естественно ввести в рассмотрение функцию f (M) = xy. Эту функцию необходимо вычислить в точке M (1,02, 2,03). За M 0 надо принять близкую точку, в которой функция легко вычисляется. Естественно положить M 0(1, 2). Тогда D x = dx = 0,02, D y = dy = 0,03. Тогда Подставляя значения, получим: df (M 0)=0,04, f (M)» f (M 0)+ df (M 0)=1+0,04=1,04. Под приближением нулевого порядка к f (M) понимается значение функции в близкой точке (в примере f (M 0)). Приближения более высоких порядков требуют привлечения высших производных, в частности, основаны на формуле Тейлора.
Вопросы для самопроверки 1. Что такое дифференциал функции нескольких переменных? 2. От скольких переменных зависит дифференциал функции n переменных?
Упражнения 1. Найти дифференциалы следующих функций в заданных точках: - u=xy+x 2, (1,1), (2,0); - u=xyz+ sin(x+y2), (-1,1,2), (0,0,3). 2. Вычислить в первом приближении - - 1,020,92, - sin 29°×tg 47°. ПРОИЗВОДНЫЕ ПО НАПРАВЛЕНИЮ Частные производные - понятие несколько искусственное. Оно "привязано" к системе координат, которую можно вводить по-разному. Производная это скорость изменения функции. Имеете смысл ввести скорость изменения функции в любом направлении. Принципиально следующие рассуждения применимы к функциям любого числа переменных, но рассмотрим трехмерный случай как наиболее важный практически. Пусть функция u (x, y, z) дифференцируема в точке M 0(x 0, y 0, z 0) и x=x 0+ t × cos a, y=y 0+ t × cos b, z=z 0+ t × cos g. Рассмотрим функцию Определение 14. Производной Применяя формулу дифференцирования сложной функции, получим:
По определению скалярного произведения где j угол между градиентом и вектором Найдем производные функции по направлениям координатных осей Пример. Найти производную функции u = x 2+ y 2 + z 2 в точке A (1,1,1) по направлению к точке B (-1,3,2). Решение. Найдем координаты вектора grad u =(2 x, 2 y, 2 z), grad u (A)=(2, 2, 2). Все подготовлено к вычислению производной по направлению.
Вопросы для самопроверки 1. Что такое производная функции в данной точке в направлении данного вектора? 2. Как вычисляется производная по направлению? 3. В каком направлении скорость изменения функции максимальная?
Упражнение 1. Найти производную функции u = x 3+ y 3+ z 3 в точке (1,1,1) в направлении - к точке (0,2,0), - градиента функции v = xyz. ФОРМУЛА ТЕЙЛОРА Формула Тейлора с остаточным членом в форме Лагранжа для функции одной переменной имеет вид:
где x некоторая точка, расположенная между x и x 0. Здесь предполагается, что точка x расположена в окрестности точки x 0, в которой функция F имеет (k +1)-ю производную. Изменяя в случае необходимости начало отсчета и масштаб, можно считать, что x 0=0, x =1. Тогда формула примет вид
Рассмотрим теперь функцию n переменных f (M) и предположим, что в некоторой окрестности точки M 0 функция f имеет все частные производные до (k +1)-го порядка и точка M принадлежит этой окрестности. Определим функцию одной переменной F (t) так:
Вычислим производные функции F (t). Это сложная функция, схема зависимости t ®(x 1,..., xn)® F (t), xi = (M 0) i + t × dxi.
далее все аналогично: Теорема 14. Пусть функция f: Rn ® R имеет все частные производные до (k +1)-го порядка в некоторой окрестности точки M 0 и точка M принадлежит этой окрестности. В окрестности существует точка x такая, что
Контрольные вопросы 1. Как выглядит формула Тейлора для функций нескольких переменных? 2. Проверьте, что формула Тейлора для функций одной переменной является частным случаем формулы для функций нескольких переменных.
Упражнения 1. Разложить функцию z = 3 xy + 4 y 2-5 x по формуле Тейлора в точке (1,2) при k = 3. 2. Записать разложение функции z = xy по формуле Тейлора до второго порядка включительно. НЕЯВНЫЕ ФУНКЦИИ Рассмотрим уравнение f (x 1, x 2,..., xn, y)=0. Будем считать, что неизвестной здесь является переменная y, т.е. речь идет о функции g (x 1, x 2,..., xn) такой, что f (x 1, x 2,..., xn, g (x 1, x 2,..., xn))=0 при (x 1, x 2,..., xn)Î V Ì Rn. Такая функция называется неявной. Таким образом, этот термин скорее относится к способу задания функции, а не к функции как таковой. Речь не идет об аналитическом описании функции g (x 1, x 2,..., xn) - даже при вполне приличной функции f (x 1, x 2,..., xn, y) такое описание чаще всего невозможно. Простой пример: 2 x + e x + y -cos y =0. Попробуйте отсюда извлечь y! Естественно поставить задачу о существовании и единственности (в некотором смысле) такой функции g (x 1, x 2,..., xn). В рамках математического анализа нас интересует локальная задача: пусть f (x 10, x 20,..., xn 0, y 0)=0, т.е. g (x 10, x 20,..., xn 0)= y 0. Существует ли функция y = g (x 1, x 2,..., xn) в некоторой окрестности точки (x 10, x 20,..., xn 0)? Единственна ли она? Какими свойствами обладает? Какую-нибудь одну точку иногда найти легко. Например, в приведенном примере это (0,0), т.е. g (0)=0. Верно ли, что функция g существует и в некоторой окрестности 0? Вопрос не так прост. Рассмотрим, например, уравнение x 2+ y 2+ u 2=1. Это уравнение сферы (рис. 4) Рассмотрим точку M 0(x 0, y 0, u 0) на сфере. В некоторой окрестности точки (x 0, y 0) неявная функция задается уравнением
Рис. 4
Утверждение выглядит довольно сложно. Теорема 19. Пусть функция f (x 1, x 2,..., xn, y) - имеет непрерывные частные производные в некоторой окрестности точки (x 10, x 20,..., xn 0, y 0) такой, что f (x 10, x 20,..., xn 0, y 0)=0; - Тогда для достаточно малого e>0 существует единственная функция g (x 1, x 2,..., xn), определенная на некоторой окрестности V точки (x 10, x 20,..., xn 0)Î Rn такая, что - f (x 1, x 2,..., xn, g (x 1, x 2,..., xn))º0; - g (x 10, x 20,..., xn 0)= y 0;
- | g (x 1, x 2,..., xn)- y 0|<e при (x 1, x 2,..., xn)Î V; - функция g (x 1, x 2,..., xn) является дифференцируемой в точке (x 10, x 20,..., xn 0). Доказательство. Рассуждения проведем для n =1 - в общем случае идейно все делается так же, только букв больше. По теореме о сохранении знака непрерывной функции, частной производной, из условия
Рис. 5
Может создаться ложное впечатление, что для каждого e построена своя функция. На самом деле в силу единственности это одна и та же функция, рассматриваемая на разных окрестностях точки x 0. Этому тезису можно придать строгий смысл, но все понятно и так. Осталось проверить дифференцируемость построенной функции. Вначале отметим, что функция g (x) непрерывна в точке x 0. Действительно, для каждого e>0 построена такая d-окрестность точки x 0, что при | x - x 0|<d справедливо неравенство | g (x)- y 0|<e, причем y 0= g (x 0), что и означает непрерывность. (На самом деле, функция g (x) непрерывна и в некоторой окрестности точки.) Рассмотрим точку x 0+D x. Пусть g (x 0+D x)= y 0+D y. Поскольку функция f (x, y) дифференцируема в точке (x 0, y 0) (частные производные непрерывные, см. теорему 9), справедливо равенство
откуда Аналогично для функций любого числа переменных. Так, если f (x, y, z)=0 и f ¢ z (x 0, y 0, z 0)¹0, то
Дополнительно к доказательству теоремы получены формулы дифференцирования неявной функции. Впрочем, производные можно вычислять и без этих формул, дифференцируя обе части уравнения, помня о неявной зависимости. Замечание. Теперь ясно, почему в точке M 0 все хорошо, а в точке M 1 нет: в первой точке главное условие выполняется, а во второй нарушается. Отдельно рассмотрим случай n = 1. Если f (x, y)=0, то в точках, где f ¢ y (x, y)¹0 задана неявная функция y (x). Ее производная вычисляется по формуле Отметим, что условие f ¢ y (x, y)¹0 достаточно, но не необходимо для существования неявной функции. Например, если f (x, y)=8 x 3- y 3, то f (0, 0)=0, f ¢ y (0,0)=0, т.е. главное условие теоремы не выполняются. В то же время, уравнение f (x, y)=0 равносильно равенству y = 2 x, функция дифференцируемая. Примеры. 1. Пусть x, y связаны соотношением Положим
Теперь покажем, как то же самое можно осуществить без использования формулы. Продифференцируем обе части равенства В результате получим линейное уравнение относительно y ¢ x, решив его, получим то же самое выражение. 2. Пусть
3. (Обратная функция). Пусть x = f (y). Найти 4. Пусть f (x, y, z)=0. Тогда Пример. 4. Вернемся к примеру 2. Вычислим Вернемся к уравнению касательной плоскости. Пусть поверхность задана уравнением f (x, y, z)=0, и на поверхности взята точка (x 0, y 0, z 0), в некоторой окрестности которой функция удовлетворяет условиям теоремы. Тогда это уравнение можно рассматривать в как неявную функцию z (x, y), определенную в некоторой окрестности точки (x 0, y 0). Частные производные этой функции вычисляются по предыдущим формулам. Уравнение касательной плоскости к поверхности имеет вид Это уравнение равноправно относительно переменных - в исходном уравнении переменная z занимала особое положение. Уравнение плоскости получено в предположении f ¢ z (x 0, y 0, z 0)¹0. Исходное уравнение f (x, y, z)=0 можно считать неявной функцией x (y, z) или y (x, z). Если хотя бы одна частная производная функции f (x, y, z) в точке (x 0, y 0, z 0) ненулевая, то можно поступить точно так же, в результате получим, как легко убедиться, то же самое уравнение касательной плоскости. Нормальный вектор к касательной плоскости (к поверхности) имеет координаты (f ¢ x (x 0, y 0, z 0), f ¢ y (x 0, y 0, z 0), f ¢ z (x 0, y 0, z 0)), т.е равен градиенту функции f (x, y, z). Таким образом, градиент обладает еще одним замечательным свойством. Надо только, чтобы градиент был отличен от 0! Точки, в которых градиент нулевой, называются особыми точками поверхности. В них касательной плоскости может и не существовать. Пример. Поверхность задана уравнением F (x, y, z)= x 2+ y 2- z 2=0. grad F = (F ¢ x, F ¢ y, F ¢ z)=(2 x, 2 y, -2 z). Градиент ненулевой в каждой точке поверхности (x 0, y 0, z 0). кроме (0,0,0), уравнение касательной плоскости (после сокращения на 2) x 0(x - x 0)+ y 0(y - y 0)- z 0(z - z 0)=0 или x 0 x - x 02+ y 0 y - y 02- z 0 z + z 02=0. Поскольку x 02+ y 02- z 02=0 (точка лежит на поверхности), окончательно получаем уравнение касательной плоскости x 0 x + y 0 y - z 0 z =0. Данная поверхность круговой конус, (0,0,0) его вершина. Разумеется, касательной плоскости к конусу в вершине не существует. Рассмотрим функцию f (x, y, z). Поверхности f (x, y, z)= c называются поверхностями уровня функции. Их можно задать и уравнениями f (x, y, z)- c =0. Нормальный вектор к поверхности, заданной таким уравнением, также является градиентом функции f (x, y, z). Это справедливо и для функции двух переменных. Например, на географические карты наносятся изогипсы - кривые, в точках которых высота над уровнем моря постоянна, т.е. линии уровня функции высоты f (x, y). Градиент этой функции в каждой точке направлен по нормали к линии уровня, нормаль легко нанести на карту. Вспомним, что направление градиента это направление наискорейшего роста функции, так что если вы хотите круче всего забираться в гору (подумайте, надо ли это делать), двигайтесь перпендикулярно касательной к изогипсе в соответствующей точке.
Вопросы для самопроверки 1. Как определяется неявная функция? 2. При каких условиях неявная функция существует? 3. Как вычисляются частные производные неявной функции? 4. Как выглядит уравнение касательной плоскости в общем случае? 5. Как связан градиент функции f (x, y, z) с нормальным вектором к поверхности f (x, z)= с?
Упражнения 1. Найти y ¢, y ¢¢ в заданной точке, если функция y (x) задана уравнением - x 2+ xy 2- y 3=1, (1,1); - 2. Найти все частные производные второго порядка функции z (x, y), заданной неявно уравнением x 2+2 y 2+3 z 2+ xy - z =9 в точке (1,-2,1). 3. Найти первые и вторые частные производные функции z (x, y), заданной равенством - F (x+y+z,x 2 +y 2 +z 2)=0, - G (x,x+y,x+y+z)=0 (функции F, G дважды дифференцируемые). 4. Доказать, что касательные плоскости к поверхности 5. Найти проекции эллипсоида x 2 + y 2 + z 2- xy = 1на координатные плоскости. 6. Найти экстремумы функции z (x, y), заданной неявно уравнением x 2 + y 2 + z 2-2 x + 2 y -4 z -10=0 НЕЯВНЫЕ ОТОБРАЖЕНИЯ Рассмотрим более общую задачу о неявном отображении. Пусть задана система уравнений
Допустим эти уравнения обращаются в равенство в точке (x 10,..., xn 0, y 10,..., ym 0)Î Rn + m. Естественно возникает вопрос: при каких условиях в некоторой окрестности точки (x 10,..., xn 0)Î Rn определены функции y 1= g 1(x 10,..., xn 0),..., ym = gm (x 10,..., xn 0) - решение системы, т.е. такие, что fi (x 10,..., xn 0, g 1(x 10,..., xn 0),..., gm (x 10,..., xn 0))=0 при i = 1,..., n? Особо отметим случай n = 0. Это означает, что из системы
на некотором множестве можно однозначно найти переменные y 1,..., ym. Если система является линейной, то ответ известен из линейной алгебры: для существования единственного решения необходима и достаточна невырожденность матрицы системы. Еще один частный случай. Пусть уравнения системы представлены в виде
(m = n). Такая система задает отображение некоторого подмножества Rm в пространство Rm. Существование неявной функции означает, что каждой точке (x 1,..., xm) из некоторого множества сопоставляется точка (y 1,..., ym). Такое отображение обратное к исходному. Теорема, естественно, должна быть похожа на теорему 19. Интригующий вопрос: как выглядит аналог (обобщение) главного условия? Теорема 20. Пусть функции fi (x 1,..., xn, y 1,..., ym) (i = 1,..., m) - имеют непрерывные частные производные в некоторой окрестности точки (x 10,..., xn 0, y 10,..., ym 0) такой, что fi (x 10,..., xn 0, y 10,..., ym 0)=0 (i = 1,..., m); - якобиан Тогда для достаточно малого e>0 существует единственное семейство функций gj (x 1, x 2,..., xn) (j =1,..., m), определенных на некоторой окрестности V точки (x 10, x 20,..., xn 0)Î Rn, со следующими свойствами: - fi (x 1, x 2,..., xn, g 1(x 1, x 2,..., xn),..., gm (x 1, x 2,..., xn))º0 при i= 1,..., m; - gj (x 10, x 20,..., xn 0)= yj 0 при j= 1,..., m; - | gj (x 1, x 2,..., xn)- yj 0|<e при (x 1, x 2,..., xn)Î U; - функции gj (x 1, x 2,..., xn) являются дифференцируемыми в точке (x 10, x 20,..., xn 0). Доказательство проведем в частном случае n = 1, m = 2. От n ничто не зависит, при m >2 доказательство основано на методе математической индукции и теории определителей. Итак, рассматриваются уравнения f 1(x, y 1, y 2)=0, f 2(x, y 1, y 2)=0, где функции f 1, f 2 имеют непрерывные частные производные в некоторой окрестности точки (x 0, y 10, y 20), координаты которой удовлетворяют данным уравнениям, Для функции f 1(x, y 1, y 2) и точки (x 0, y 10, y 20) выполняются все условия теоремы 19 относительно переменной y 1, т.е. в некоторой окрестности точки (x 0, y 20) существует единственная дифференцируемая функция y 1= h (x, y 2) такая, что y 10= h (x 0, y 20), f 1(x, h (x, y 2), y 2)=0, причем Вычислим
Подставляя в последнее выражение для
Из главного условия теоремы следует, что - y 20= g 2(x 0), y 10= h (x 0, y 20)= h (x 0, g 2(x 0))= g 1(x 0);
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 110; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.160.154 (0.159 с.) |
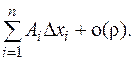 Теорема 7 утверждает, что
Теорема 7 утверждает, что 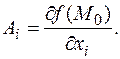 При этом все приращения аргументов предполагаются независимыми, т.е. приращение D f (M) определено на некоторой окрестности (еще раз напомним, что все понятия дифференциального исчисления локальные!) точки (0,0,...,0) в пространстве приращений (D x 1,...,D x n). Дифференциал определяется как и для функции одной переменной.
При этом все приращения аргументов предполагаются независимыми, т.е. приращение D f (M) определено на некоторой окрестности (еще раз напомним, что все понятия дифференциального исчисления локальные!) точки (0,0,...,0) в пространстве приращений (D x 1,...,D x n). Дифференциал определяется как и для функции одной переменной.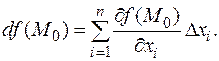
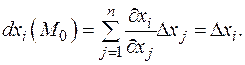 Таким образом, дифференциал можно записать в виде
Таким образом, дифференциал можно записать в виде 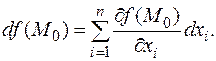 Эта замена может показаться искусственной, позднее выяснится, что она имеет глубокий смысл.
Эта замена может показаться искусственной, позднее выяснится, что она имеет глубокий смысл.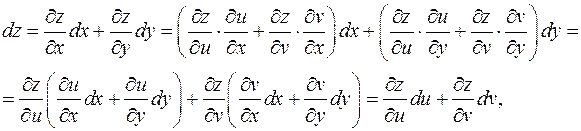 что и требовалось. Этот результат следствие удачной формы записи дифференциала и линейности суперпозиции линейных функций.
что и требовалось. Этот результат следствие удачной формы записи дифференциала и линейности суперпозиции линейных функций.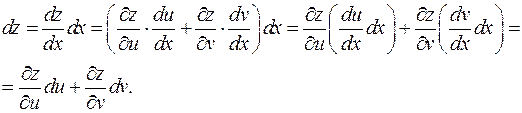 Теорема доказана.
Теорема доказана.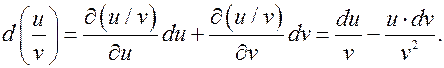 Остается привести правую часть равенства к общему знаменателю.
Остается привести правую часть равенства к общему знаменателю.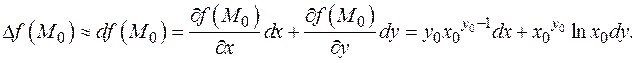
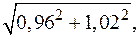
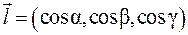 единичный вектор, заданный направляющими косинусами, т.е. косинусами углов, образованных вектором с осями координат. Параметрические уравнения прямой, проходящей через точку M 0 параллельно вектору
единичный вектор, заданный направляющими косинусами, т.е. косинусами углов, образованных вектором с осями координат. Параметрические уравнения прямой, проходящей через точку M 0 параллельно вектору 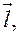 задается параметрическими уравнениями
задается параметрическими уравнениями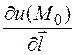 функции u (x, y, z) в точке M 0(x 0, y 0, z 0) в направлении вектора
функции u (x, y, z) в точке M 0(x 0, y 0, z 0) в направлении вектора  называется
называется 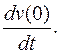
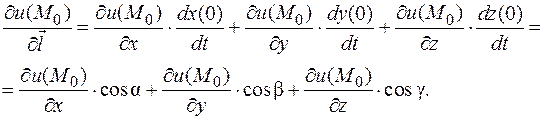 Последнее выражение является скалярным произведением двух векторов:
Последнее выражение является скалярным произведением двух векторов: 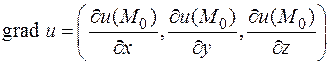 .
.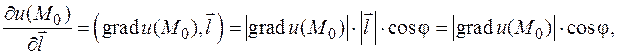
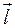 , последнее равенство справедливо, поскольку вектор
, последнее равенство справедливо, поскольку вектор 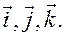 Например,
Например, 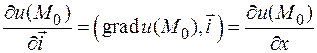 , аналогично с другими осями. То есть, определение согласовано с «обычными» частными производными.
, аналогично с другими осями. То есть, определение согласовано с «обычными» частными производными.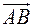 : (-2,2,1). Единичный вектор
: (-2,2,1). Единичный вектор 
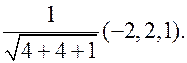
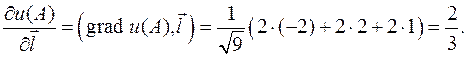
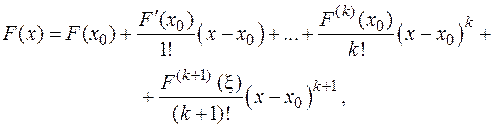
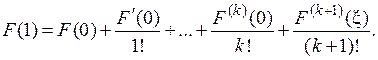
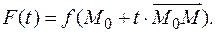 Функция F (t) обладает свойствами, при которых справедлива формула Тейлора. Предварительно вычислим производные этой функции. Пусть координаты точек M 0 и M соответственно (x 1,..., xn) и (x 1+ dx 1,..., xn + dxn), т.е. изменения координат представлены в виде дифференциалов переменных.
Функция F (t) обладает свойствами, при которых справедлива формула Тейлора. Предварительно вычислим производные этой функции. Пусть координаты точек M 0 и M соответственно (x 1,..., xn) и (x 1+ dx 1,..., xn + dxn), т.е. изменения координат представлены в виде дифференциалов переменных.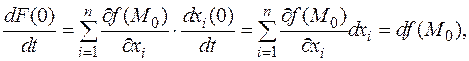
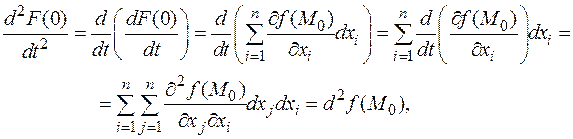
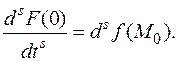 Таким образом, приходим к следующему выводу.
Таким образом, приходим к следующему выводу.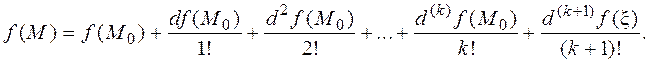 В качестве (dx 1,..., dxn) принимаются координаты вектора
В качестве (dx 1,..., dxn) принимаются координаты вектора 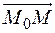 .Какследует из приведенных рассуждений, точка x расположена на отрезке [ M 0, M ].
.Какследует из приведенных рассуждений, точка x расположена на отрезке [ M 0, M ].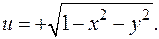 Иная ситуация с точкой M 1(x 1, y 1, u 1): ни в какой окрестности точки (x 1, y 1) неявная функция не определена (вспомним, что окрестность это шар или параллелепипед с центром в точке, для плоскости - круг или прямоугольник). В чем разница между точками?
Иная ситуация с точкой M 1(x 1, y 1, u 1): ни в какой окрестности точки (x 1, y 1) неявная функция не определена (вспомним, что окрестность это шар или параллелепипед с центром в точке, для плоскости - круг или прямоугольник). В чем разница между точками?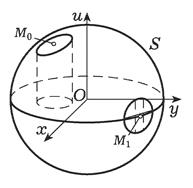
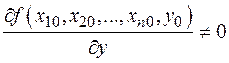 (это условие главное!).
(это условие главное!).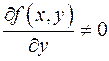 (будем для определенности считать производную положительной) следует, что производная положительная и в некоторой окрестности точки (x 0, y 0). Пусть в этой окрестности расположена кубическая (квадратная) окрестность точки (x 0, y 0) {(x, y):| x - x 0|< a, | y - y 0|< a }. «Достаточно малое e» из формулировки теоремы означает теперь «не превосходящее a». Выберем положительное e£ a. Рассмотрим функцию f (x, y) на отрезке, соединяющем точки (x 0, y 0-e), (x 0, y 0+e). Поскольку частная производная функции f (x, y) по y положительная, то функция f (x 0, y) на этом отрезке возрастает с ростом y. При этом f (x 0, y 0)=0. Это означает, что f (x 0, y 0-e)<0, f (x 0, y 0+e)>0. Функция f (x, y) имеет непрерывные частные производные, значит, она непрерывна. Отсюда по теореме о сохранении знака непрерывной функции следует, что при некотором d>0 на интервале u с концами (x 0-d, y 0-e), (x 0+d, y 0-e) функция f (x, y) отрицательная, а на интервале v с концами (x 0-d, y 0+e), (x 0+d, y 0+e) положительная. Окрестность V из формулировки теоремы это d-окрестность точки x 0. Пусть x 0-d< x < x 0+d. По построению, точки (x, y 0-e), (x, y 0+e) расположены соответственно на интервалах u и v, т.е. функция f (x, y) в этих точках соответственно отрицательная и положительная. В силу непрерывности, по теореме о промежуточном значении в некоторой точке (x, g (x)) функция f (x, y) обращается в 0. Такая точка единственная, поскольку на интервале с концами (x, y 0-e), (x, y 0+e) функция f (x, y) возрастающая. Функция g (x) построена. Построение проиллюстрировано на рис. 5.
(будем для определенности считать производную положительной) следует, что производная положительная и в некоторой окрестности точки (x 0, y 0). Пусть в этой окрестности расположена кубическая (квадратная) окрестность точки (x 0, y 0) {(x, y):| x - x 0|< a, | y - y 0|< a }. «Достаточно малое e» из формулировки теоремы означает теперь «не превосходящее a». Выберем положительное e£ a. Рассмотрим функцию f (x, y) на отрезке, соединяющем точки (x 0, y 0-e), (x 0, y 0+e). Поскольку частная производная функции f (x, y) по y положительная, то функция f (x 0, y) на этом отрезке возрастает с ростом y. При этом f (x 0, y 0)=0. Это означает, что f (x 0, y 0-e)<0, f (x 0, y 0+e)>0. Функция f (x, y) имеет непрерывные частные производные, значит, она непрерывна. Отсюда по теореме о сохранении знака непрерывной функции следует, что при некотором d>0 на интервале u с концами (x 0-d, y 0-e), (x 0+d, y 0-e) функция f (x, y) отрицательная, а на интервале v с концами (x 0-d, y 0+e), (x 0+d, y 0+e) положительная. Окрестность V из формулировки теоремы это d-окрестность точки x 0. Пусть x 0-d< x < x 0+d. По построению, точки (x, y 0-e), (x, y 0+e) расположены соответственно на интервалах u и v, т.е. функция f (x, y) в этих точках соответственно отрицательная и положительная. В силу непрерывности, по теореме о промежуточном значении в некоторой точке (x, g (x)) функция f (x, y) обращается в 0. Такая точка единственная, поскольку на интервале с концами (x, y 0-e), (x, y 0+e) функция f (x, y) возрастающая. Функция g (x) построена. Построение проиллюстрировано на рис. 5.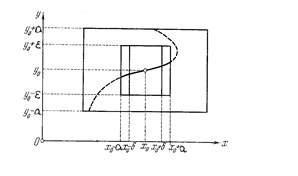
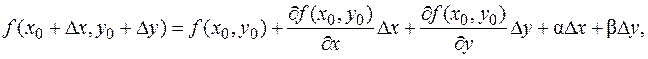 где a,b®0 при D x, D y ®0 или, поскольку D y ®0 при D x ®0 вследствие непрерывности функции g (x), можно считать, что a,b®0 при D x ®0. Далее, f (x 0, y 0)=0, f (x 0+D x, y 0+D y)= f (x 0+D x, g (x 0+D x))=0. Тогда
где a,b®0 при D x, D y ®0 или, поскольку D y ®0 при D x ®0 вследствие непрерывности функции g (x), можно считать, что a,b®0 при D x ®0. Далее, f (x 0, y 0)=0, f (x 0+D x, y 0+D y)= f (x 0+D x, g (x 0+D x))=0. Тогда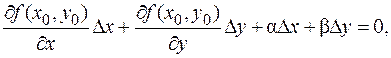
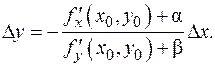 При достаточно малых D x знаменатель дроби отличен от 0, поскольку частная производная ненулевая (главное условие!), а b®0 при D x ®0; предел дроби при D x ®0 равен
При достаточно малых D x знаменатель дроби отличен от 0, поскольку частная производная ненулевая (главное условие!), а b®0 при D x ®0; предел дроби при D x ®0 равен 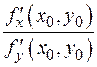 , поскольку a,b®0 при D x ®0. По определению предела
, поскольку a,b®0 при D x ®0. По определению предела 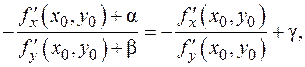 где g®0 при D x ®0. Получили равенство
где g®0 при D x ®0. Получили равенство 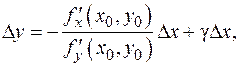 которое означает дифференцируемость функции g (x)= y (x) в точке x 0, причем
которое означает дифференцируемость функции g (x)= y (x) в точке x 0, причем 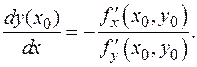
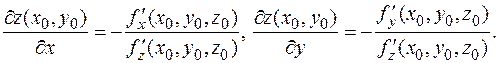
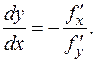
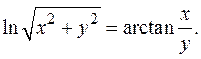 Найти y ¢ x.
Найти y ¢ x.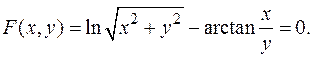
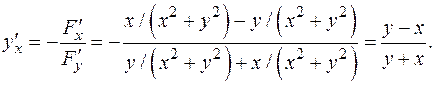
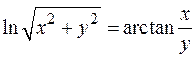 по x, учитывая зависимость, y (x). Получаем
по x, учитывая зависимость, y (x). Получаем 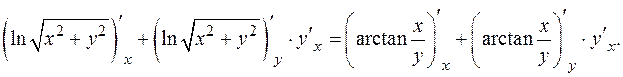
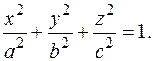 Найти частные производные z по x, y. Положим
Найти частные производные z по x, y. Положим 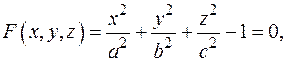 вычислим производные
вычислим производные 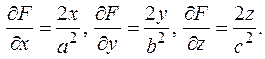 Отсюда,
Отсюда,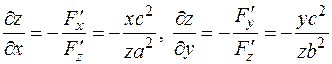 при z ¹ 0.
при z ¹ 0.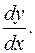
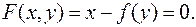
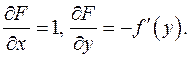 Отсюда,
Отсюда, 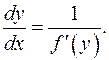 Это известная из первой части курса математического анализа формула для вычисления производной обратной функции. Иначе ее можно записать в виде
Это известная из первой части курса математического анализа формула для вычисления производной обратной функции. Иначе ее можно записать в виде 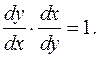
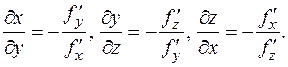 Отсюда
Отсюда 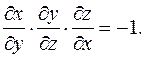
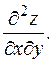 Из решения примера 2,
Из решения примера 2, 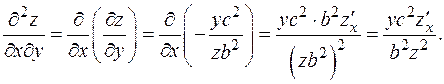 Подставляя сюда z ¢ x, окончательно получим:
Подставляя сюда z ¢ x, окончательно получим: 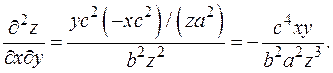 Как и следовало ожидать, в формулу переменные x и y входят равноправно. Такие простые наблюдения позволяют избежать некоторых ошибок!
Как и следовало ожидать, в формулу переменные x и y входят равноправно. Такие простые наблюдения позволяют избежать некоторых ошибок!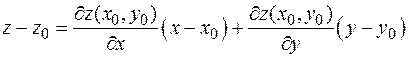 (см. п. 6). Подставляя сюда выражения для частных производных, получим
(см. п. 6). Подставляя сюда выражения для частных производных, получим 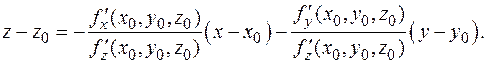 Умножив это равенство на частную производную по z, после переноса всех слагаемых в левую часть получим уравнение касательной плоскости в форме
Умножив это равенство на частную производную по z, после переноса всех слагаемых в левую часть получим уравнение касательной плоскости в форме 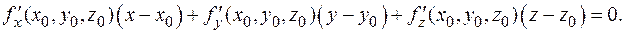
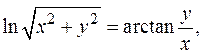 (0,1).
(0,1).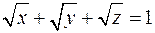 отсекают на координатных осях отрезки, сумма которых постоянна.
отсекают на координатных осях отрезки, сумма которых постоянна.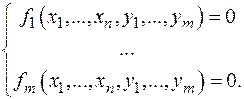
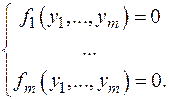
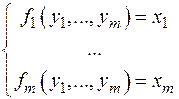
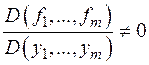 в точке (x 10,..., xn 0, y 10,..., ym 0) (главное условие для этого случая).
в точке (x 10,..., xn 0, y 10,..., ym 0) (главное условие для этого случая).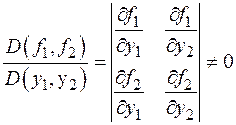 в точке (x 0, y 10, y 20). В определителе есть ненулевые элементы (В противном случае определитель равен 0). Пусть для определенности отличен от 0 элемент в первой строке и в первом столбце.
в точке (x 0, y 10, y 20). В определителе есть ненулевые элементы (В противном случае определитель равен 0). Пусть для определенности отличен от 0 элемент в первой строке и в первом столбце.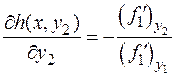 .Введем обозначение F (x, y 2)= f 2(x, h (x, y 2), y 2).
.Введем обозначение F (x, y 2)= f 2(x, h (x, y 2), y 2).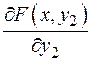 . F (x, y 2) сложная функция от y 2. Применяя формулу дифференцирования, получим:
. F (x, y 2) сложная функция от y 2. Применяя формулу дифференцирования, получим: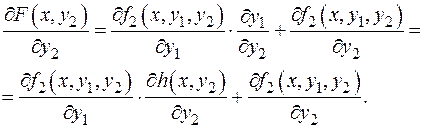
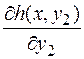 , получем
, получем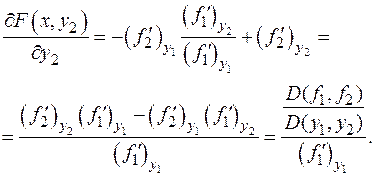
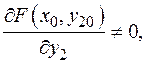 а тогда по теореме 19 в некоторой окрестности точки x 0 однозначно определена дифференцируемая функция y 2= g 2(x) такая, что F (x, g 2(x))=0, y 20= g 2(x 0). Тогда y 1= h (x, y 2)= h (x, g 2(x)). Пусть g 1(x)= h (x, g 2(x)). Построенные функции обладают нужными свойствами:
а тогда по теореме 19 в некоторой окрестности точки x 0 однозначно определена дифференцируемая функция y 2= g 2(x) такая, что F (x, g 2(x))=0, y 20= g 2(x 0). Тогда y 1= h (x, y 2)= h (x, g 2(x)). Пусть g 1(x)= h (x, g 2(x)). Построенные функции обладают нужными свойствами:


