
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные производные и дифференцируемостьСодержание книги
Поиск на нашем сайте
Производная - одно из основных понятий математического анализа. Содержательно это мгновенная скорость изменения функции, т.е. предел отношения приращения функции к приращению аргумента, когда последнее стремится к 0. Но для функции нескольких переменных приращений аргумента несколько. Так, для двух переменных D f (x 0, y 0)= f (x 0+D x, y 0+D y)- f (x 0, y 0), т.е. здесь два приращения аргументов. Для большего числа переменных их еще больше. Как быть? Понятие производной как бы расщепляется. Введем в рассмотрение частные приращения D x f (x 0, y 0)= f (x 0+D x, y 0)- f (x 0, y 0), D y f (x 0, y 0)= f (x 0, y 0+D y)- f (x 0, y 0), т.е. рассматриваем функцию по отдельности на прямых, параллельных координатным осям. Для функции n переменных таких приращений n. Определение 10. Частными производными функции f (x, y) в точке (x 0, y 0) по переменным x, y называются
если пределы существуют. У функции столько частных производных, сколько переменных. Для функции одной переменной использовалось обозначение Для вычисления частных производных о функции надо знать совсем мало: какова она на прямых, параллельных осям координат и проходящих через точку (x 0, y 0) в некоторой окрестности точки. В частности, частные производные функции, равной 0 на осях координат и 1 в остальных точках плоскости (или пространства любой размерности) равны 0 в начале координат. Этот пример далее пригодится. Примеры вычисления частных производных. Никакой специальной таблицы частных производных, разумеется, не существует. Вычисляется обычная производная, все переменные кроме одной считаются постоянными. 1. Аналогично, 2. z = xy. Особенность этой функции в том, что по переменной x она степенная, а по переменной y показательная. Для функций одной переменной важную роль играло понятие дифференцируемости функции. Оно состояло в существовании числа A и бесконечно малой при D x ®0 функции a(D x) таких, что D f (x 0)= A D x +a(D x)×D x. Было доказано, что дифференцируемость равносильна существованию производной, причем
Определение 11. Функция f (x, y) называется дифференцируемой, если существуют числа A, B и функции a(D x, D y), b(D x, D y) такие, что a(0, 0)=b(0, 0)=0, D f (x 0, y 0)= f (x 0+D x, y 0+D y)- f (x 0, y 0)= A D x + B D y+ a(D x, D y)D x+ b(D x, D y)D y. Смысл этого определения в том, что приращение функции есть сумма линейной функции от D x, D y и совсем крошечного «довеска» (бесконечно малой высшего порядка). Полезно следующее техническое утверждение. Теорема 7. Сумму a(D x, D y)D x + b(D x, D y)D y можно представить в виде о(r), где Напомним, что бесконечно малые в точке a функции f (x), g (x) находятся в отношении f (x)=о(g (x)), если (при естественных ограничениях) Доказательство. |a(D x, D y)D x + b(D x, D y)D y | /r£|a(D x, D y)|×(||D x |/r)+|b(D x, D y)|×(| D y | /r)£ £|a(D x, D y)|+|b(D x, D y)|, т.е. по свойствам бесконечно малых функций a(D x, D y)D x + b(D x, D y)D y =о(r). С другой стороны, о(r) это c(r)×r, где c(r)®0 при r®0. Положим Связь дифференцируемости с частными производными есть, но не такая тесная, как для функций одной переменной. В частности, справедлива Теорема 8. Если функция f (x, y) дифференцируема в точке (x 0, y 0), то частные производные существуют, причем Доказательство. Частное приращение D x f (x 0, y 0) дифференцируемой функции равно A D x + a(D x, 0)D x. Отсюда,
Обратное неверно: в отличие от функций одной переменной частные производные могут существовать у функции недифференцируемой! Для этого заметим, что
а это означает, что дифференцируемая функция является непрерывной. Разумеется, непрерывная функция не обязательно дифференцируемая - такие примеры есть и для функций одной переменной (в частности, | x | в точке 0). Но частные производные могут существовать и у функции, не являющейся непрерывной! Пример уже был описан: функция, равная 0 на осях координат и 1 в остальных точках плоскости.
Тем не менее, усиленная версия обратного утверждения справедлива! Теорема 9. Если частные производные функции f (x, y) существуют в некоторой окрестности точки (x 0, y 0) и непрерывны в точке (x 0, y 0), то функция в этой точке дифференцируемая. Доказательство. Пользуясь одним из сильнейших приемов математики (прибавить и отнять то же самое), запишем: D f (x 0, y 0)= f (x 0+D x, y 0+D y)- f (x 0, y 0)= =(f (x 0+D x, y 0+D y)- f (x 0, y 0+D y))+(f (x 0, y 0+D y)- f (x 0, y 0)). Выражение в первой скобке это приращение функции при фиксированном втором аргументе, т.е. приращение функции одной переменной. Производная этой функции есть частная производная по аргументу x. По теореме Лагранжа существует такое число c (D x, D y), расположенное между x 0 и x 0+D x, для которого Точка (c (D x, D y), y 0+D y) (при D x, D y >0, в других случаях все аналогично) расположена в прямоугольнике x 0£ x £ x 0+D x, y 0£ y £ y 0+D y. Отсюда по теореме о милиционерах (c (D x, D y), y 0+D y)®(x 0, y 0) при D x ®0, D y ®0. В силу непрерывности частных производных
где Аналогично Подстановка полученных выражений в D f (x 0, y 0) завершает доказательство. Функция, удовлетворяющая условию теоремы, называется непрерывно дифференцируемой. Рассмотренные свойства функций связаны следующим образом: {непрерывно дифференцируемые}Ì{дифференцируемые}Ì {имеющие частные производные}. Для функций нескольких переменных все включения строгие, для функций одной переменной второе включение является равенством множеств. Для отображений полезна следующая конструкция. Пусть f =(f 1, f 2,..., fm): Rn ® Rm, причем все функции fi дифференцируемы в точке M 0. Такое отображение называется дифференцируемым. Из частных производных естественно сформировать матрицу
Если m=n, то матрица Якоби квадратная, ее определитель называется якобианом отображения. Это понятие играет важную роль в теории кратных интегралов. Якобиан обозначается так: Далее нам встретится матрица Якоби для функции f: Rn ® R, ее можно считать вектором
Вопросы для самопроверки 1. Что такое частное приращение функции нескольких переменных? 2. Что такое частная производная функции нескольких переменных? Сколько частных производных может иметь функция n переменных в данной точке? 3. Следует ли из существования частных производных непрерывность функции в некоторой точке? 4. Какая функция называется дифференцируемой? 5. Следует ли из дифференцируемости непрерывность функции? 6. Следует ли из дифференцируемости существование частных производных? 7. Какая функция называется непрерывно дифференцируемой? 8. Сформулируйте достаточное условие дифференцируемости функции. 9. Что такое матрица Якоби отображения? 10. Что такое якобиан отображения? У каких отображений он определен? 11. Что такое градиент функции?
Упражнения 1. Найти частные производные функций - z= ln(x+ e xy), - u=xyz, - z = sin(x 2- y 2). 2. Найти матрицу Якоби отображения
3. Доказать, что функция - непрерывна на всей плоскости, - имеет частные производные на всей плоскости, - не дифференцируема в точке (0,0). Таким образом, требование непрерывности частных производных в теореме 9 исключить нельзя. 4. Доказать, что функция - имеет на всей плоскости частные производные, - частные производные разрывны в точке (0,0), - функция дифференцируема в точке (0,0). Тем самым, условия теоремы 9 достаточные, но не необходимые для дифференцируемости.
|
|||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 101; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.57.158 (0.009 с.) |

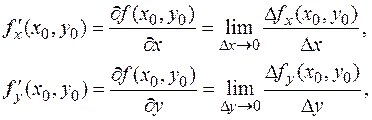
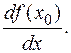 Различие обозначений играет важную роль. В частности последнее обозначение можно рассматривать как отношение дифференциалов, для частных производных это неверно.
Различие обозначений играет важную роль. В частности последнее обозначение можно рассматривать как отношение дифференциалов, для частных производных это неверно.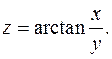 Для вычисления производной
Для вычисления производной 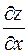 считаем, что переменная y фиксирована (на первых порах ее можно заменить на более привычное обозначение постоянной, например, a). Используя обычное правило дифференцирования сложной функции, получим:
считаем, что переменная y фиксирована (на первых порах ее можно заменить на более привычное обозначение постоянной, например, a). Используя обычное правило дифференцирования сложной функции, получим: 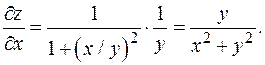
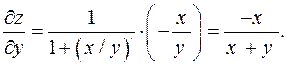
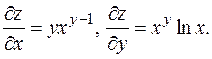
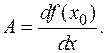 Определение дифференцируемости функции нескольких переменных приведем для двумерного случая, обобщение очевидно.
Определение дифференцируемости функции нескольких переменных приведем для двумерного случая, обобщение очевидно.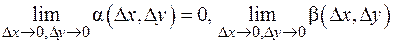 , для которых
, для которых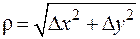 - длина вектора отклонения от базовой точки (x 0, y 0) и наоборот.
- длина вектора отклонения от базовой точки (x 0, y 0) и наоборот.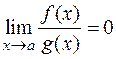 .
.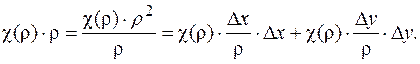
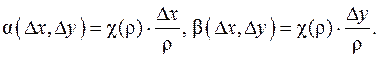 a(D x, D y)®0 при D x, D y ®0 (или, что то же самое при r®0 - можно использовать окрестности разных видов!), поскольку
a(D x, D y)®0 при D x, D y ®0 (или, что то же самое при r®0 - можно использовать окрестности разных видов!), поскольку 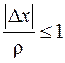 . Аналогично с b(D x, D y). Для функций n переменных определение дифференцируемости аналогично:
. Аналогично с b(D x, D y). Для функций n переменных определение дифференцируемости аналогично: 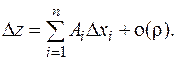
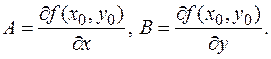
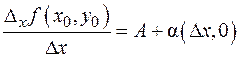 при D x ®0. Из свойств функции a(D x, D y) получаем:
при D x ®0. Из свойств функции a(D x, D y) получаем: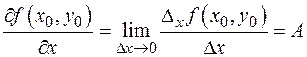 , что и требовалось.
, что и требовалось.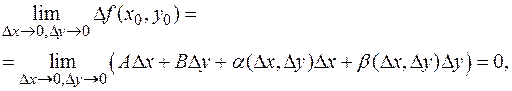
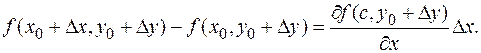
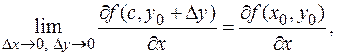 т.е.
т.е.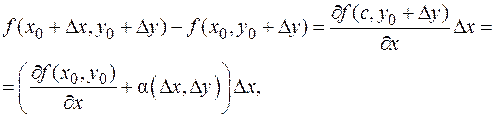
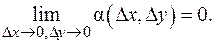
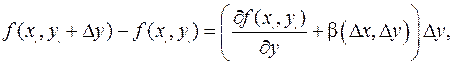 где
где 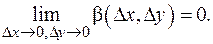
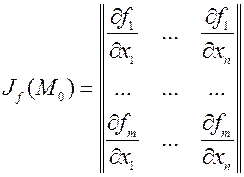 , она называется матрицей Якоби отображения в точке M 0 (все производные вычисляются в этой точке). Карл Якоби, в честь которого назван этот объект - немецкий математик 19 века, его родной брат Борис (в русской транскрипции) - знаменитый физик, значительную часть жизни работавший в России.
, она называется матрицей Якоби отображения в точке M 0 (все производные вычисляются в этой точке). Карл Якоби, в честь которого назван этот объект - немецкий математик 19 века, его родной брат Борис (в русской транскрипции) - знаменитый физик, значительную часть жизни работавший в России.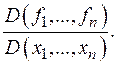
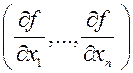 . Этот вектор называется градиентом функции. Он обладает рядом замечательных свойств, о которых будет сказано далее. Если m=n= 1, то матрица Якоби содержит единственный элемент - производную функции, а якобиан - значение этой производной.
. Этот вектор называется градиентом функции. Он обладает рядом замечательных свойств, о которых будет сказано далее. Если m=n= 1, то матрица Якоби содержит единственный элемент - производную функции, а якобиан - значение этой производной.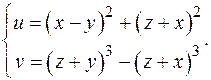
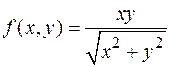 при x 2+ y 2>0, f (0,0)=0
при x 2+ y 2>0, f (0,0)=0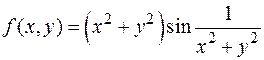 при x 2+ y 2>0, f (0,0)=0
при x 2+ y 2>0, f (0,0)=0


