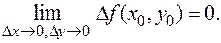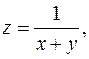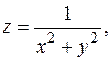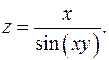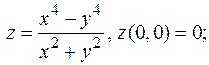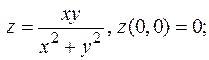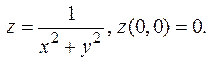Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывные функции нескольких переменныхСодержание книги
Поиск на нашем сайте
Непрерывность функции одной переменной имеет наглядное описание: график функции, непрерывной на интервале, можно изобразить не отрывая руки. Формально непрерывность функции нескольких переменных определяется так же, как и для функций одной переменной, но столь наглядный образ ей сопоставить трудно. Смысл тот же: достаточно малому изменению аргумента соответствует сколь угодно малое изменение значения функции. Определение 9. Функция f (M) называется непрерывной в точке M 0, если она определена в некоторой (не проколотой!) окрестности M 0 и Вставляя сюда определения предела 8 и 8', получим следующие определения непрерывности: - для любой последовательности точек { M (1), M (2),..., M ( k ),...}, сходящейся к M 0, числовая последовательность { f (M (1)), f (M (2)),..., f (M ( k )),...} сходится к f (M 0), - ("e>0) ($d>0): (M Î U d(M 0)))Þ(| f (M)- f (M 0)|<e). Для еще одного определения непрерывности функции потребуется понятие приращения функции D f (M 0)= f (M)- f (M 0). Из определения 9 следует: непрерывность означает, что В определении предполагается, что точка M 0 - внутренняя точка области определения функции. Говорят и о непрерывности в граничных точках множества. Чтобы не возникало противоречия, будем считать, что функция определена на некотором открытом множестве, объемлющем рассматриваемое множество. Определение непрерывного отображения аналогично. Далее рассматриваются функции непрерывные на множествах, т.е. во всех точках множества. При переходе к нескольким переменным теряет смысл классификация точек разрыва, т.е. точек, в которых непрерывность функции теряется. Для функции одной переменной она основывалась на односторонних пределах, а для функций нескольких переменных, как уже отмечалось, это понятие теряет смысл. Правда, аналог устранимого разрыва есть (см пример 1 из 3 раздела). Сохраняются многие свойства непрерывных функций одной переменной. В частности - сумма, разность, произведение, отношение (в точках, где делитель ненулевой) непрерывных функций непрерывны; - если функция непрерывна и ненулевая в точке M 0, то в некоторой окрестности точки она сохраняет знак (это свойство имеет такую шуточную интерпретацию: если в водоеме выныривает лысый человек, то над водой не может оказаться одна макушка, обязательно там окажется и часть лысины); - непрерывная функция на компактном множестве ограничена; - непрерывная функция на компактном множестве принимает минимальное и максимальное значения. Последние два свойства опираются на теорему 2 (Больцано-Вейерштрасса). Доказательства этих свойств почти дословно повторяют доказательства тех же свойств функций, непрерывных на отрезке. Отрезок множество компактное! Для дальнейшего полезно расширить понятие непрерывности. Пусть отображение f: Rn ® Rm таково, что все функции fi непрерывны в точке M Î Rn. Такое отображение f называется непрерывным в точке M. Теорема 5. Суперпозиция непрерывных отображений непрерывна. Подробнее. Пусть отображение f: Rn ® Rm непрерывно в точке M 0Î Rn, g: Rm ® Rp непрерывно в точке f (M 0). Тогда отображение f ๐ g непрерывно в точке M 0. Доказательство. Воспользуемся определением непрерывности через последовательности. Пусть { M (1), M (2),..., M ( k ),...} - произвольная последовательность в Rn, сходящаяся к M 0. В силу непрерывности f справедливо f (M ( k ))® f (M 0). Непрерывность g дает (f ๐ g)(M ( k ))= g (f (M ( k )))® g (f (M 0))=(f ๐ g)(M 0). Следствием произвольности последовательности в Rn является непрерывность отображения f ๐ g. Отметим, что при n = m = p = 1это обычная теорема о непрерывности сложной функции. Теорема 6. Пусть функция g: V ® R, где V Ì Rn - связное множество. Если M, N Î V, то функция g принимает на V любое значение между g (M)и g (N). Для функций одной переменной в качестве V рассматривался отрезок. Это множество связное. Доказательство. Соединим точки M, N непрерывной кривой, т.е. построим непрерывное отображение f:[0,1]® V такое, что f (0)= M, f (1)= N. Тогда f ๐ g:[0,1]® R непрерывное отображение в силу теоремы 5, причем (f ๐ g)(0)= g (M), (f ๐ g)(1)= g (N). По "обычной" теореме о промежуточном значении отображение f ๐ g принимает все значения между (f ๐ g)(0) и (f ๐ g)(1), т.е. между g (M)и g (N). Как связана непрерывность функции нескольких переменных с непрерывностью на прямых? Из непрерывности функции на всех прямых, проходящих через некоторую точку, не следует непрерывность функции в этой точке. Пример (с некоторыми изменениями) уже был: f (x, y)=1 при y = x 2, x ¹ 0 и f (x, y)=0 во всех остальных точках плоскости. Подробности оставляем читателю.
Вопросы для самопроверки 1. Приведите различные определения непрерывной функции нескольких переменных. 2. Что такое приращение функции нескольких переменных? От скольких переменных оно зависит? 3. Является ли непрерывной суперпозиция непрерывных отображений? 4. Какие свойства непрерывных функций сохраняются при переходе от одной переменной к нескольким переменным? 5. Для функций, заданных на каких множествах, справедливы свойства непрерывных функций, аналогичные свойствам функций одной переменной?
Упражнения 1. Найти точки разрыва функций - - - Есть ли среди них устранимые разрывы? 2. Исследовать на непрерывность в точке (0,0) следующие функции: - - -
|
||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 158; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.95.233 (0.006 с.) |

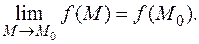
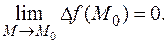 Для двух переменных (то же можно выписать и для большего числа переменных): если M 0(x 0, y 0), M (x 0+D x, y 0+D y), то непрерывность записывается в виде
Для двух переменных (то же можно выписать и для большего числа переменных): если M 0(x 0, y 0), M (x 0+D x, y 0+D y), то непрерывность записывается в виде