
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные и дифференциалы высших порядков
Частная производная
Так выглядит схема частных производных первого и второго порядка функции двух переменных. Пример. f (x, y)= xy.
Смешанные производные оказались равными. Возникает вопрос: это случайность? Вообще говоря, это не всегда так. Рассмотрим пример функции, у которой одна из смешанных производных существует, а другая нет. Модификация этого примера дает пример функции, обе смешанные производной которой существуют, но не равны. Пусть
Тем не менее, для широкого класса достаточно «хороших» функций смешанные производные совпадают. Теорема 13. Пусть в некоторой окрестности точки M 0(x 0, y 0) функция f (x, y) имеет частные производные Доказательство. Выберем такое число h, что квадрат [ x 0, x 0+ h ]´[ y 0, y 0+ h ] расположен в окрестности, о которой говорится в условии теоремы. Рассмотрим величину W= f (x 0+ h, y 0+ h)+ f (x 0, y 0)- f (x 0+ h, y 0)- f (x 0, y 0+ h). Это есть сумма значений функции в двух противоположных вершинах квадрата минус сумму значений функции в двух других противоположных вершинах квадрата. Запишем W так: (f (x 0+ h, y 0+ h)- f (x 0+ h, y 0))-(f (x 0, y 0+ h)- f (x 0, y 0)). Если принять j(x)= f (x, y 0+ h)- f (x, y 0), то W=j(x 0 + h)-j(x 0). По формуле конечных приращений W=j'(q)× h, где qÎ[ x 0, x 0+ h ]. Производные функции j(x) это частные производные функции f по x, т.е.
Представим теперь W в форме (f (x 0+ h, y 0+ h)- f (x 0, y 0+ h))-(f (x 0+ h, y 0)- f (x 0, y 0)). Проведя те же рассуждения, но в другом порядке (сначала по y, затем по x), получим Для производных высших порядков утверждение теоремы также справедливо. Следствие. Пусть функция n переменных имеет непрерывные частные производные m порядка в некоторой точке. Тогда эти производные не зависят от порядка дифференцирования. Замечание. Условия здесь избыточные, но на практике этого хватает. Доказательство. Прежде всего, достаточно доказать, что производная не меняется при перемене двух соседних дифференцирований. Действительно, любую перестановку символов можно получить из данной с помощью перестановок соседей. Например, из перестановки (3,1,4,5,1,2) надо получить перестановку тех же цифр (2,5,3,1,1,4). Последовательность перестановок соседей: (3,1,4,5,1,2)®(3,1,4,5,2,1)®(3,1,4,2,5,1)®(3,1,2,4,5,1)®(3,2,1,4,5,1)® Поскольку функция имеет непрерывные частные производные m порядка, то она имеет непрерывные частные производные и меньших порядков. Докажем следствие на примере, в общем случае рассуждения те же самые. Рассмотрим две частные производные Отсюда следует, что можно выпмсывать одни и те же переменные дифференцирования подряд. Например, производные из нашего примера можно записать так: Приведем примеры вычисления частных производных второго порядка сложных функций, частично заданных функциональными символами. 1. Пусть u = j(xyz, x 2+ y 2+ z 2). Необходимо найти
2. Рассмотрим теперь пример 5 из п. 7 z =f (x + y)+ g (x - y). Найдем вторые частные производные.
Функция z (x, y) при произвольных функциях f, g удовлетворяет уравнению Перейдем к понятию дифференциалов высших порядков. Заметим, что (первый) дифференциал
Таким образом, второй дифференциал является квадратичной функцией от dx 1,..., dxn. Дифференциалы более высоких порядков определяются индуктивно: если определен дифференциал k -го порядка d k u, то дифференциал (k +1)-го порядка d k +1 u равен d (d k u). Отсюда, например Если учесть равенство смешанных производных, то получаем для функций двух переменных:
Эти формулы похожи на формулы для квадрата и куба суммы. Так же будет и для любого числа переменных, и для дифференциалов любых порядков (проверяется по индукции). Это наблюдение позволяет формализовать построение дифференциалов следующим образом. Введем оператор - символ - возвести оператор в k -ю степень - «умножить» обе части полученного формального равенства на u. Дифференциал второго порядка функций одной переменной не был инвариантен относительно замены независимых переменных на зависимые от тех или иных параметров. Для функции нескольких переменных это тоже верно. Приведем соответствующую (довольно длинную) выкладку для второго дифференциала функции двух переменных.
Если x, y независимые переменные, то их вторые дифференциалы d 2 x. d 2 y обращаются в 0. Соответственно получаем известную формулу. Это верно и тогда, когда x, y зависимые переменные, но их вторые дифференциалы равны нулю, что означает линейную зависимость x, y от своих аргументов.
Вопросы для самопроверки 1. Как определяются производные высших порядков? 2. Какие производные называются смешанными? 3. При каких условиях смешанные производные не зависят от порядка дифференцирования? 4. Как определяются дифференциалы высших порядков? 5. В каком случае форма дифференциала второго порядка инвариантна относительно замены независимых переменных на зависимые?
Упражнения 1. Вычислить 2. Вычислить 3. Найти производные второго прядка от функций - f (x, xy, xyz), - 4. Доказать, что функция u = x j(x + y)+ y y(x + y) удовлетворяет уравнению 5. Доказать, что функция u = x j[ x + y(y)] удовлетворяет уравнению 6. Найти дифференциалы первого и второго порядка функций - u = f (x 2+ y 2+ z 2), - u = g (ax 2, by 2)
ФОРМУЛА ТЕЙЛОРА Формула Тейлора с остаточным членом в форме Лагранжа для функции одной переменной имеет вид:
где x некоторая точка, расположенная между x и x 0. Здесь предполагается, что точка x расположена в окрестности точки x 0, в которой функция F имеет (k +1)-ю производную. Изменяя в случае необходимости начало отсчета и масштаб, можно считать, что x 0=0, x =1. Тогда формула примет вид
Рассмотрим теперь функцию n переменных f (M) и предположим, что в некоторой окрестности точки M 0 функция f имеет все частные производные до (k +1)-го порядка и точка M принадлежит этой окрестности. Определим функцию одной переменной F (t) так: Вычислим производные функции F (t). Это сложная функция, схема зависимости t ®(x 1,..., xn)® F (t), xi = (M 0) i + t × dxi.
далее все аналогично: Теорема 14. Пусть функция f: Rn ® R имеет все частные производные до (k +1)-го порядка в некоторой окрестности точки M 0 и точка M принадлежит этой окрестности. В окрестности существует точка x такая, что
Контрольные вопросы 1. Как выглядит формула Тейлора для функций нескольких переменных? 2. Проверьте, что формула Тейлора для функций одной переменной является частным случаем формулы для функций нескольких переменных.
Упражнения 1. Разложить функцию z = 3 xy + 4 y 2-5 x по формуле Тейлора в точке (1,2) при k = 3. 2. Записать разложение функции z = xy по формуле Тейлора до второго порядка включительно.
|
||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.236.62 (0.025 с.) |
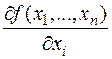 является функцией n переменных, значит, от нее можно взять производную
является функцией n переменных, значит, от нее можно взять производную 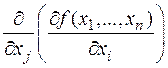 , она называется частной производной второго порядка по соответствующим переменным. Обозначается аналогично производным функций одной переменной
, она называется частной производной второго порядка по соответствующим переменным. Обозначается аналогично производным функций одной переменной 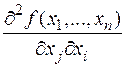 . Если j = i, то обозначение упрощается:
. Если j = i, то обозначение упрощается: 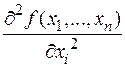 . При j ¹ i производная называется смешанной. Производные высших порядков определяются индуктивно: если определены производные k -го порядка, то производные (k +1)-го порядка это производные от производных k -го порядка.
. При j ¹ i производная называется смешанной. Производные высших порядков определяются индуктивно: если определены производные k -го порядка, то производные (k +1)-го порядка это производные от производных k -го порядка.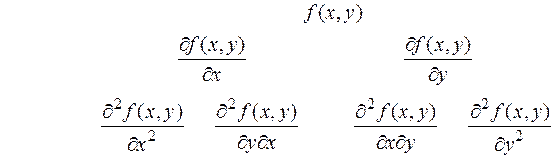
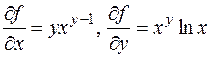
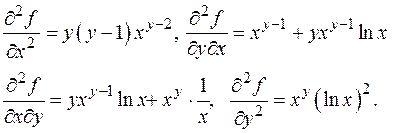
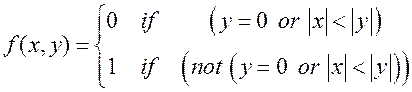
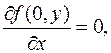 поскольку f (x, y)=0 при x Î(-| y |,| y |) (y ¹ 0), f (x, 0)=0 при любом x. Отсюда
поскольку f (x, y)=0 при x Î(-| y |,| y |) (y ¹ 0), f (x, 0)=0 при любом x. Отсюда 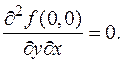 При этом
При этом 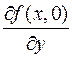 не существует при x ¹ 0 (функция разрывная). А тогда не существует и
не существует при x ¹ 0 (функция разрывная). А тогда не существует и 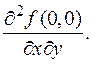
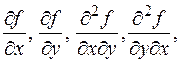 причем производные второго порядка непрерывны в точке M 0. Тогда
причем производные второго порядка непрерывны в точке M 0. Тогда 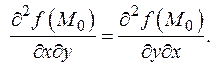 Про вторые производные
Про вторые производные 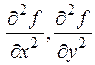 ничего не утверждается, даже существование!
ничего не утверждается, даже существование!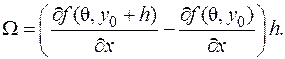 Обозначим через
Обозначим через 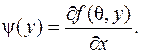 Выражение в скобках это приращение функции y(y) на отрезке [ y 0, y 0+ h ]. Как и ранее, по формуле конечных приращений существует такое число cÎ[ y 0, y 0+ h ], для которого
Выражение в скобках это приращение функции y(y) на отрезке [ y 0, y 0+ h ]. Как и ранее, по формуле конечных приращений существует такое число cÎ[ y 0, y 0+ h ], для которого 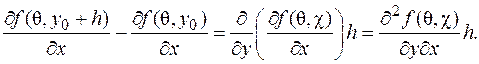 Отсюда
Отсюда 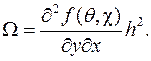 Поскольку вторая производная по условию непрерывна в точке M 0(x 0, y 0), справедливо равенство
Поскольку вторая производная по условию непрерывна в точке M 0(x 0, y 0), справедливо равенство 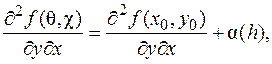 где
где 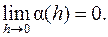 Таким образом,
Таким образом, 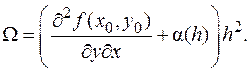
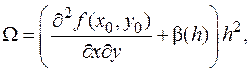
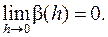 Приравняв два выражения для W, получим:
Приравняв два выражения для W, получим: 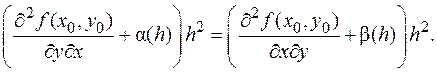 Сократив на h 2 и перейдя к пределу при h ®0, установим нужное равенство смешанных производных.
Сократив на h 2 и перейдя к пределу при h ®0, установим нужное равенство смешанных производных.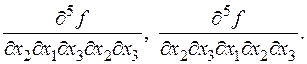 Пусть
Пусть 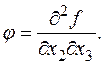 По теореме 13
По теореме 13 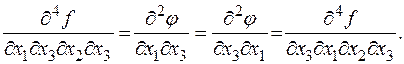 Осталось взять от обеих частей производную по x 2.Следствие доказано.
Осталось взять от обеих частей производную по x 2.Следствие доказано.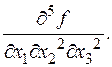 Сумма «степеней» в знаменателе должна равняться «степени» в числителе.
Сумма «степеней» в знаменателе должна равняться «степени» в числителе.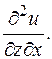 Ранее (пример 4 из п. 7) получено, что
Ранее (пример 4 из п. 7) получено, что 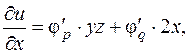 где p = xyz, q = x 2 + y 2 + z 2. Надо найти
где p = xyz, q = x 2 + y 2 + z 2. Надо найти 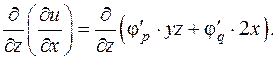 Применяя правила дифференцирования, получим:
Применяя правила дифференцирования, получим: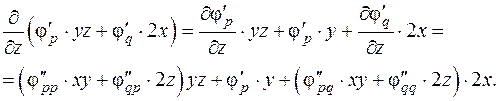
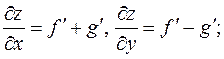
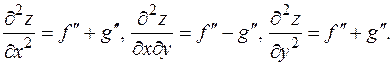
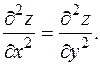 Это уравнение описывает колебание струны. Подробно теория таких уравнений излагается в курсе дифференциальных уравнений с частными производными. В частности, там установлено, что других решений у этого уравнения нет.
Это уравнение описывает колебание струны. Подробно теория таких уравнений излагается в курсе дифференциальных уравнений с частными производными. В частности, там установлено, что других решений у этого уравнения нет.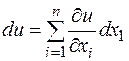 дифференцируемой функции u (x 1,..., xn) зависит от 2 n (пока) независимых переменных x 1,..., xn и приращений dx 1,..., dxn. Вторым дифференциалом d 2 u называется дифференциал от первого дифференциала, рассматриваемого как функция от n переменных: x 1,..., xn (т.е. d (d xi)=0). Таким образом,
дифференцируемой функции u (x 1,..., xn) зависит от 2 n (пока) независимых переменных x 1,..., xn и приращений dx 1,..., dxn. Вторым дифференциалом d 2 u называется дифференциал от первого дифференциала, рассматриваемого как функция от n переменных: x 1,..., xn (т.е. d (d xi)=0). Таким образом,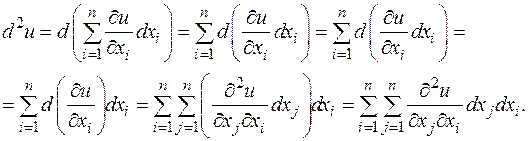
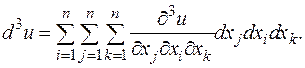
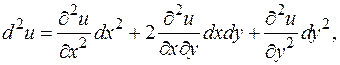
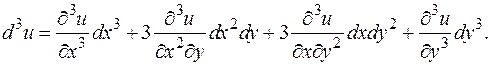
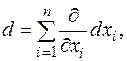 который сам по себе ничего не значит. Если умножить его формально на u, т.е. приписать u на свободные места (после d с левой стороны и после ¶ с правой), получим формулу для дифференциала. А для получения дифференциала k -го порядка, как следует из приведенных наблюдений, надо
который сам по себе ничего не значит. Если умножить его формально на u, т.е. приписать u на свободные места (после d с левой стороны и после ¶ с правой), получим формулу для дифференциала. А для получения дифференциала k -го порядка, как следует из приведенных наблюдений, надо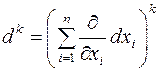 (умножение осуществляется по обычным правилам алгебры),
(умножение осуществляется по обычным правилам алгебры),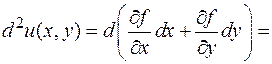
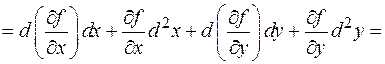
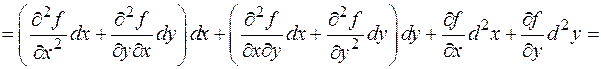
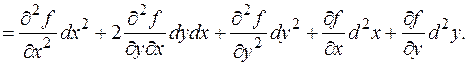
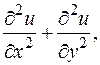 если
если 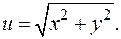
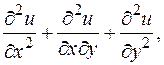 если
если 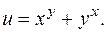
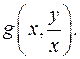
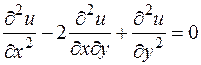
 (j и y - дважды дифференцируемые функции).
(j и y - дважды дифференцируемые функции).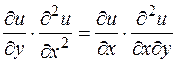
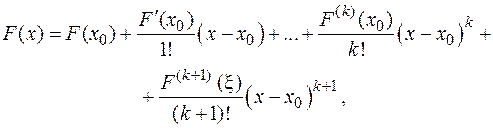
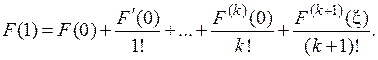
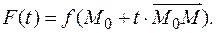 Функция F (t) обладает свойствами, при которых справедлива формула Тейлора. Предварительно вычислим производные этой функции. Пусть координаты точек M 0 и M соответственно (x 1,..., xn) и (x 1+ dx 1,..., xn + dxn), т.е. изменения координат представлены в виде дифференциалов переменных.
Функция F (t) обладает свойствами, при которых справедлива формула Тейлора. Предварительно вычислим производные этой функции. Пусть координаты точек M 0 и M соответственно (x 1,..., xn) и (x 1+ dx 1,..., xn + dxn), т.е. изменения координат представлены в виде дифференциалов переменных.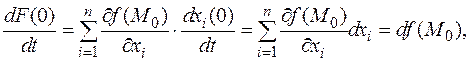
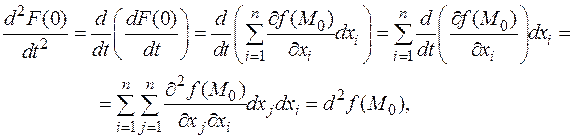
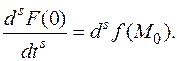 Таким образом, приходим к следующему выводу.
Таким образом, приходим к следующему выводу.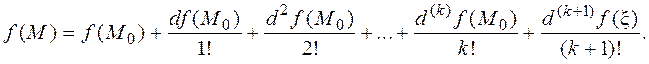 В качестве (dx 1,..., dxn) принимаются координаты вектора
В качестве (dx 1,..., dxn) принимаются координаты вектора 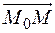 .Какследует из приведенных рассуждений, точка x расположена на отрезке [ M 0, M ].
.Какследует из приведенных рассуждений, точка x расположена на отрезке [ M 0, M ].


