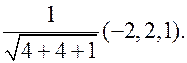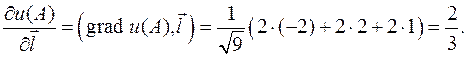Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцирование сложных отображений
В математическом анализе функций одной переменной важную роль имело правило дифференцирования сложной функции
или сокращенно Правило дифференцирования композиций отображений имеет следующий вид. Теорема 11. Пусть f: Rn ® Rk, g: Rk ® Rm, причем отображение f дифференцируемо в точке M 0, g дифференцируемо в точке f (M 0). Тогда отображение f ๐ g: Rn ® Rm дифференцируемо в точке M 0, причем Jf ๐ g (M 0)= Jg (f (M 0))× Jf (M 0), т.е. матрица Якоби композиции отображений равна произведению матриц Якоби сомножителей. Прежде, чем доказывать теорему, приведем примеры. 1. f: R 2® R 2, g: R 2® R 1, т.е. заданы функции y 1(x 1, x 2), y 2(x 1, x 2) (отображение f), z (y 1, y 2) (отображение g). Тогда f ๐ g это отображение R 2® R 1.
По правилу умножения матриц получим:
Разумеется, ни о каком «сокращении» символов ¶ речи быть не может. 2. f: R 1® R 2, g: R 2® R 1, заданы функции y 1(x), y 2(x) (отображение f), z (y 1, y 2) (отображение g). Тогда f ๐ g это отображение R 1® R 1.
Обратите внимание на использование прямых букв d в обозначениях производных. Они используются там, где функции зависят от одной переменной. 3. f: R 1® R 2, g: R 2® R 2, заданы функции y 1(x), y 2(x) (отображение f), z 1(y 1, y 2), z 2(y 1, y 2) (отображение g). Тогда f ๐ g это отображение R 1® R 2.
Этот пример показывает, что доказывать теорему нужно только при m = 1 - компоненты точки в Rm можно рассматривать по отдельности. 4. Самый простой случай f: R 1® R 1, g: R 1® R 1. Заданы функции y (x) (отображение f), z (y) (отображение g). Тогда f ๐ g это отображение R 1® R 1.
формула дифференцирования сложной функции одной переменной. Естественно, все согласуется. Доказательство. Отмечалось, что достаточно рассмотреть случай m = 1. Доказательство проведем при n = k = 2, в общем случае принципиальных изменений нет. Итак, даны функции y 1(x 1, x 2), y 2(x 1, x 2), дифференцируемые в точке (a, b) (для упрощения записи используем буквы без индексов) и функция z (y 1, y 2), дифференцируемая в точке (c, d), где c = y 1(a, b), d = y 2(a, b). Придадим переменным x 1 и x 2 приращения D x 1, D x 2. При этом переменные y 1, y 2 получат приращения D y 1, D y 2. Важно, что D y 1,D y 2®0 при D x 1, D x 2®0 в силу непрерывности дифференцируемых функций Поскольку функции y 1(x 1, x 2), y 2(x 1, x 2) дифференцируемые в точке (a, b), справедливы равенства
где Реакцией на приращения D y 1, D y 2 является приращение D z функции z (y 1, y 2). Из дифференцируемости этой функции следует, что
где g,d®0 при D y 1,D y 2®0. Подставляя в последнее равенство выражения для D y 1 и D y 2 и сгруппировав слагаемые, получим:
Примеры. 1. Приведем вначале стандартный пример, какие часто встречаются в задачниках. Он чисто учебный, практически бесполезный. Пусть u = x 2 y 3+2 y, x = sin t, y = e t. Найти Целесообразно сначала записать зависимости схематически: t ®(x, y)® u. Используются прямые буквы d, поскольку суперпозиция приводит к зависимости u от одной переменной t. Формула дифференцирования имеет в этой ситуации такой вид:
2. Еще один пример такого типа. Пусть u = pq 2, p = x + y 2, q = x 2 + y. Найти Схематически: (x, y)®(p, q)® u. Получаем:
Здесь справедливо замечание из предыдущего примера. 3. Более интересны ситуации, когда промежуточные переменные целесообразно вводить в процессе решения. Пример. Необходимо найти частные производные функции По формуле дифференцирования сложной функции
Аналогично вычисляется производная по y. 4. Наиболее интересны задачи, в которых присутствуют произвольные функции. Особенно важны такие задачи для теории дифференциальных уравнений в частных производных - важнейшего инструмента описания многих реальных процессов.
Пусть надо найти частные производные функции u = j(xyz, x 2+ y 2+ z 2). Введем переменные p= xyz, q = x 2+ y 2+ z 2. Тогда u = j(p, q). Схема (x, y, z)®(p, q)® u. Отсюда 5. Пусть z =f (x + y)+ g (x - y). Обозначим p= x + y, q = x - y. Тогда z =f (p)+ g (q). Схема почти та же, что и в примере 4.
У производных функций f и g нет индексов, поскольку каждая из них зависит от одной переменной (p и q соответственно), разночтения не возникает. 6. Формула для производной сложной функции нескольких переменных позволяет вычислять и некоторые производные функции одной переменной. В качестве примера рассмотрим степенно-показательную функцию y = f (x) g ( x ). Производные таких функций ранее вычислялись с использованием логарифмирования. Можно поступить иначе. Пусть p = f (x), q = g (x). Тогда y =p q. Схема x ®(p, q)® y.
7. В завершение более сложный пример. z = xyf (x 2 y, g (3 x +2 y)). Как и выше, обозначим p = x 2 y, q = g (3 x +2 y). Схема здесь такая: (x, y)®(x, y,p, q)® z. Неудачно, что одни и те же переменные x, y встречаются в двух звеньях цепочки. Чтобы избежать путаницы, временно заменим x, y на u, v в той части функции, которая не входит в p, q. Получим z = uvf (p, q), u = x, v = y, схема (x, y)®(u, v,p, q)® z. Применяя формулу дифференцирования, получим:
здесь при формировании последнего слагаемого еще раз использовалась формула дифференцирования сложной функции. Теперь восстановим исходные переменные:
Производная по y вычисляется аналогично. Разумеется, встречаются и более сложные ситуации.
Вопросы для самопроверки 1. Как формулируется общая теорема о дифференцируемости сложного отображения? 2. Как вычислить производную сложной функции нескольких переменных?
Упражнения 1. Найти частные производные функций 2. Найти частные производные функции 3. Доказать, что функция 4.. Доказать, что функция z = f (x 2+ y 2) (f - дифференцируемая функция) удовлетворяет уравнению 5. Доказать, что касательные плоскости к конусу 6. Доказать, что нормали к поверхности вращения ДИФФЕРЕНЦИАЛ По определению 11 функция n переменных f (M) называется дифференцируемой в точке M 0, если ее приращение D f (M 0) представимо в виде Определение 13. Дифференциалом называется линейная функция от (D x 1,...,D x n) вида
Таким образом, из приращения выделена линейная часть. Говорят о «главной линейной части приращения» в том смысле, что отброшена бесконечно малая более высокого порядка. Такая терминология неприменима при нулевом дифференциале. В силу независимости приращений переменных для каждого аргумента xi (производные от xi по другим переменным равны 0) справедливо равенство
Геометрический смысл дифференциала функции двух переменных аналогичен смыслу дифференциала функции одной переменной: он равен приращению касательной плоскости к графику функции в точке M 0 при изменении аргументов на d x 1 и d x 2. Следующее свойство дифференциала является принципиально важным, в частности, при вычислении интегралов. Теорема 12. Форма дифференциала инвариантна, т.е. формула имеет тот же вид, если переменные x 1,..., x n являются функции от каких-либо переменных. Доказательство. Рассмотрим два частных случая, в общем случае выкладки принципиально те же самые. 1. (x, y)®(u, v)® z, считаем, что x, y независимые переменные.
2. Отдельно рассмотрим случай суперпозиции x ®(u, v)® z, поскольку у функций одной переменной есть специфика.
Это свойство позволяет на новом уровне получить известные для функций одной переменной формулы для дифференциалов d (u ± v)= du ± dv, d (uv)= du × v + dv u, d (u/v)=(du × v - dv u)/ v 2. Докажем, например, третью формулу.
Как и для функций одной переменной, дифференциал можно использовать для приближенных вычислений (говорят, в первом приближении). Принимаем, что D f (M 0)» df (M 0). Пример. Вычислить в первом приближении величину 1,022,03. Для этого естественно ввести в рассмотрение функцию f (M) = xy. Эту функцию необходимо вычислить в точке M (1,02, 2,03). За M 0 надо принять близкую точку, в которой функция легко вычисляется. Естественно положить M 0(1, 2). Тогда D x = dx = 0,02, D y = dy = 0,03. Тогда Подставляя значения, получим: df (M 0)=0,04, f (M)» f (M 0)+ df (M 0)=1+0,04=1,04. Под приближением нулевого порядка к f (M) понимается значение функции в близкой точке (в примере f (M 0)). Приближения более высоких порядков требуют привлечения высших производных, в частности, основаны на формуле Тейлора.
Вопросы для самопроверки 1. Что такое дифференциал функции нескольких переменных? 2. От скольких переменных зависит дифференциал функции n переменных?
Упражнения 1. Найти дифференциалы следующих функций в заданных точках: - u=xy+x 2, (1,1), (2,0); - u=xyz+ sin(x+y2), (-1,1,2), (0,0,3). 2. Вычислить в первом приближении - - 1,020,92, - sin 29°×tg 47°. ПРОИЗВОДНЫЕ ПО НАПРАВЛЕНИЮ
Частные производные - понятие несколько искусственное. Оно "привязано" к системе координат, которую можно вводить по-разному. Производная это скорость изменения функции. Имеете смысл ввести скорость изменения функции в любом направлении. Принципиально следующие рассуждения применимы к функциям любого числа переменных, но рассмотрим трехмерный случай как наиболее важный практически. Пусть функция u (x, y, z) дифференцируема в точке M 0(x 0, y 0, z 0) и x=x 0+ t × cos a, y=y 0+ t × cos b, z=z 0+ t × cos g. Рассмотрим функцию Определение 14. Производной Применяя формулу дифференцирования сложной функции, получим:
По определению скалярного произведения где j угол между градиентом и вектором Найдем производные функции по направлениям координатных осей Пример. Найти производную функции u = x 2+ y 2 + z 2 в точке A (1,1,1) по направлению к точке B (-1,3,2). Решение. Найдем координаты вектора grad u =(2 x, 2 y, 2 z), grad u (A)=(2, 2, 2). Все подготовлено к вычислению производной по направлению.
Вопросы для самопроверки 1. Что такое производная функции в данной точке в направлении данного вектора? 2. Как вычисляется производная по направлению? 3. В каком направлении скорость изменения функции максимальная?
Упражнение 1. Найти производную функции u = x 3+ y 3+ z 3 в точке (1,1,1) в направлении - к точке (0,2,0), - градиента функции v = xyz.
|
||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.168.172 (0.075 с.) |
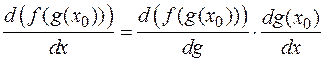
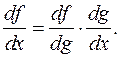 Равенство показывает, что выражение dg формально можно сократить. Это важная особенность теории функций одной переменной.
Равенство показывает, что выражение dg формально можно сократить. Это важная особенность теории функций одной переменной.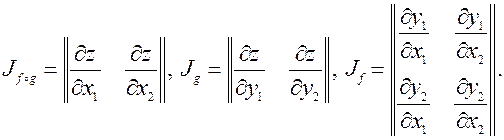
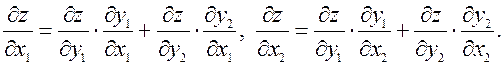
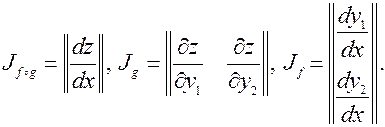 Отсюда
Отсюда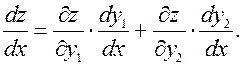
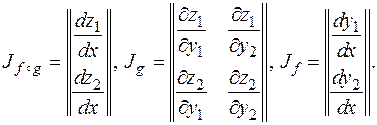 Получаем
Получаем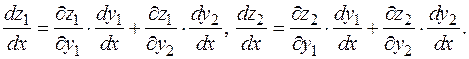
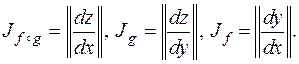 Получаем
Получаем 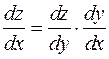 -
-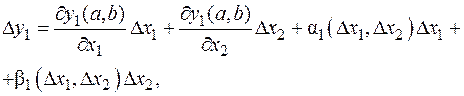
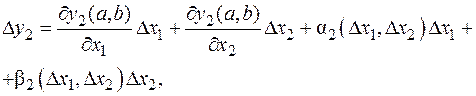
 a1, a2, b1, b2®0 при D x 1, D x 2®0.
a1, a2, b1, b2®0 при D x 1, D x 2®0.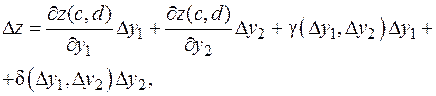
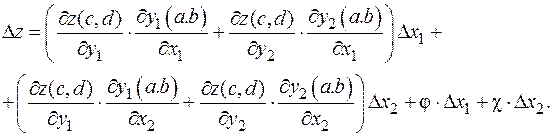 Опишем вид величин j, c (ограничимся j, для c аналогично).
Опишем вид величин j, c (ограничимся j, для c аналогично).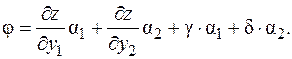 Здесь не приводятся аргументы функций в правой части, чтобы не усложнять формулу. При D x 1, D x 2®0 предел j равен 0, поскольку в первых двух слагаемых числа - значения производных умножаются на бесконечно малые, а последние два слагаемых - произведения бесконечно малых. Таким образом, приращение D z (a, b) представлено в форме из определения 11, т.е. функция z (x, y) дифференцируема в точке (a, b). Частные производные
Здесь не приводятся аргументы функций в правой части, чтобы не усложнять формулу. При D x 1, D x 2®0 предел j равен 0, поскольку в первых двух слагаемых числа - значения производных умножаются на бесконечно малые, а последние два слагаемых - произведения бесконечно малых. Таким образом, приращение D z (a, b) представлено в форме из определения 11, т.е. функция z (x, y) дифференцируема в точке (a, b). Частные производные  равны множителям при D x 1, D x 2 в первых слагаемых выражения для D z, это соответствует утверждению теоремы.
равны множителям при D x 1, D x 2 в первых слагаемых выражения для D z, это соответствует утверждению теоремы.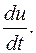
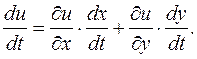 Подставляя заданные функции, получаем:
Подставляя заданные функции, получаем: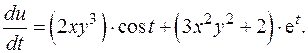 Теперь можно сюда подставить функции x и y, но непонятно, почему нельзя было это сделать с самого начала.
Теперь можно сюда подставить функции x и y, но непонятно, почему нельзя было это сделать с самого начала.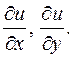
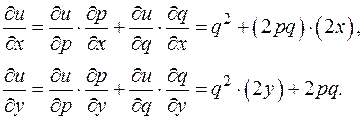
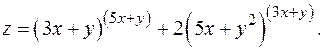 Целесообразно ввести переменные u = 3 x + y, v = 5 x + y 2. Тогда z = uv +2 vu. Схематически: (x, y)®(u, v)® z.
Целесообразно ввести переменные u = 3 x + y, v = 5 x + y 2. Тогда z = uv +2 vu. Схематически: (x, y)®(u, v)® z.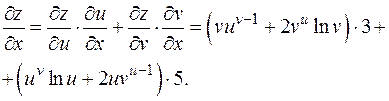
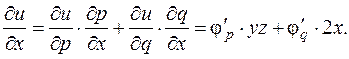 Аналогично вычисляются частные производные по y и z. Производные функции jдалее не преобразуются.
Аналогично вычисляются частные производные по y и z. Производные функции jдалее не преобразуются.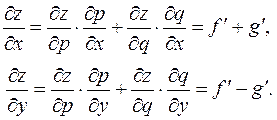
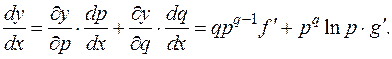
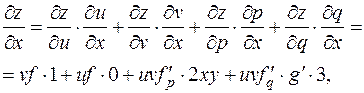
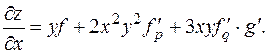
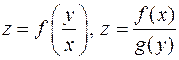 (f, g - дифференцируемые функции).
(f, g - дифференцируемые функции).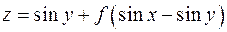 (f - дифференцируемая функция).
(f - дифференцируемая функция).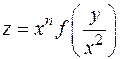 (f - дифференцируемая функция) удовлетворяет уравнению
(f - дифференцируемая функция) удовлетворяет уравнению 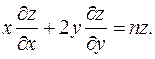
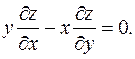
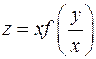 проходят через его вершину.
проходят через его вершину.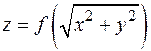 пересекают ось вращения.
пересекают ось вращения.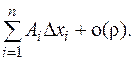 Теорема 7 утверждает, что
Теорема 7 утверждает, что 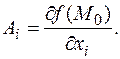 При этом все приращения аргументов предполагаются независимыми, т.е. приращение D f (M) определено на некоторой окрестности (еще раз напомним, что все понятия дифференциального исчисления локальные!) точки (0,0,...,0) в пространстве приращений (D x 1,...,D x n). Дифференциал определяется как и для функции одной переменной.
При этом все приращения аргументов предполагаются независимыми, т.е. приращение D f (M) определено на некоторой окрестности (еще раз напомним, что все понятия дифференциального исчисления локальные!) точки (0,0,...,0) в пространстве приращений (D x 1,...,D x n). Дифференциал определяется как и для функции одной переменной.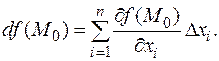
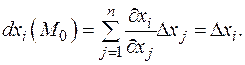 Таким образом, дифференциал можно записать в виде
Таким образом, дифференциал можно записать в виде 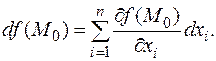 Эта замена может показаться искусственной, позднее выяснится, что она имеет глубокий смысл.
Эта замена может показаться искусственной, позднее выяснится, что она имеет глубокий смысл.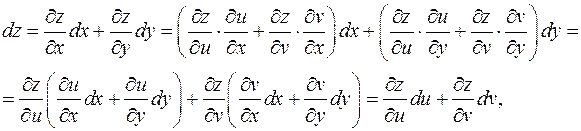 что и требовалось. Этот результат следствие удачной формы записи дифференциала и линейности суперпозиции линейных функций.
что и требовалось. Этот результат следствие удачной формы записи дифференциала и линейности суперпозиции линейных функций.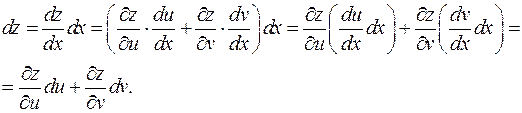 Теорема доказана.
Теорема доказана.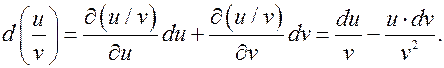 Остается привести правую часть равенства к общему знаменателю.
Остается привести правую часть равенства к общему знаменателю.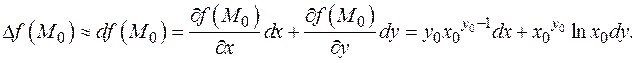
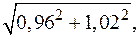
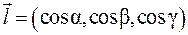 единичный вектор, заданный направляющими косинусами, т.е. косинусами углов, образованных вектором с осями координат. Параметрические уравнения прямой, проходящей через точку M 0 параллельно вектору
единичный вектор, заданный направляющими косинусами, т.е. косинусами углов, образованных вектором с осями координат. Параметрические уравнения прямой, проходящей через точку M 0 параллельно вектору 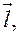 задается параметрическими уравнениями
задается параметрическими уравнениями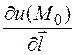 функции u (x, y, z) в точке M 0(x 0, y 0, z 0) в направлении вектора
функции u (x, y, z) в точке M 0(x 0, y 0, z 0) в направлении вектора  называется
называется 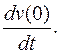
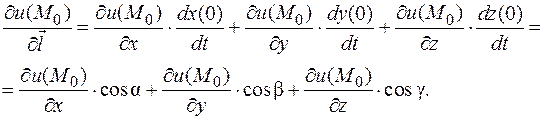 Последнее выражение является скалярным произведением двух векторов:
Последнее выражение является скалярным произведением двух векторов: 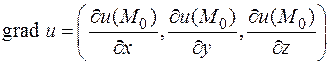 .
.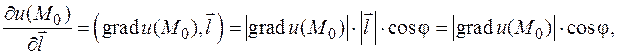
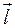 , последнее равенство справедливо, поскольку вектор
, последнее равенство справедливо, поскольку вектор 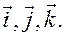 Например,
Например, 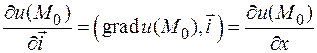 , аналогично с другими осями. То есть, определение согласовано с «обычными» частными производными.
, аналогично с другими осями. То есть, определение согласовано с «обычными» частными производными.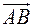 : (-2,2,1). Единичный вектор
: (-2,2,1). Единичный вектор