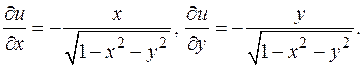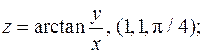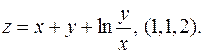Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Касательная плоскость и нормаль к поверхности
Представления о касательной прямой к кривой, касательной плоскости к поверхности воспринимаются нами с детства на интуитивном уровне. Например, мы читали: "Пуля его только коснулась". В школе говорили о касательной к окружности, касательной плоскости к сфере. В общем случае понятия эти весьма непростые. Прежде всего, понятия эти локальные, т.е. при изменении кривой или поверхности за пределами малой окрестности точки касательная не меняется. Это соображение показывает, что наивное представление о касательной как о прямой (плоскости), имеющей с кривой (поверхностью) одну общую точку некорректно. Так, касательной к прямой (плоскости) естественно считать саму эту прямую (плоскость). Разумеется, говорить здесь о единственности несколько странно. В то же время, у параболы y = x 2 в точке 0 касательной естественно считать ось абсцисс. Но единственную общую точку с параболой имеет и ось ординат! Две касательные? Нехорошо. Лучше всего согласуется с интуицией следующее представление: если рассматривать в микроскоп окрестность точки на кривой, то мы практически увидим в некоторых случаях отрезок прямой, которую естественно назвать касательной. То же можно сказать и о поверхности, если представить 3d-микроскоп. Это представление надо формализовать. Обычно определяют касательную к кривой как предельное положение секущей. Это надо как-то интерпретировать, поскольку в курсе анализа изучаются пределы числовых функций, а о функциях, значениями которых являются прямые, речи не было. Поэтому предпочтительно дать определение касательной несколько иначе. Обозначим через Определение 120. Пусть y = f (x). Прямая l называется касательной к графику функции в точке M 0 = (x 0, f (x 0)), если - прямая проходит через точку M 0 - Здесь a - направляющий вектор прямой l, M = (x, f (x)). В этом определении говорится о пределе числовой функции. в то же время, оговорка, касающаяся угла, не совсем удобно. Лучше использовать нормаль n к прямой l. Вторая часть определения примет форму
Было доказано, что касательная к графику дифференцируемой функции существует, ее уравнение y = f (x 0)+ f ' (x 0)(x - x 0). Предстоит перенести эту конструкцию на поверхности. Рассмотрим поверхность, заданную уравнением u = f (M)= f (x, y) и точку N 0(x 0, y 0, u 0) на поверхности (u 0= f (x 0, y 0)). Первая идея построения касательной плоскости основана на том, что поскольку в пространстве для задания плоскости нужны три точки, выбрать на поверхности какие-нибудь две точки "вблизи" N 0, провести плоскость через три точки, затем выбранные две точки устремить к N 0 и посмотреть, к чему приближается эта плоскость. Ничего не получится! Рассмотрим, например, сферу x 2+ y 2+ u 2=1 и точку на поверхности (0,0,1). Ясно, что касательная плоскость к сфере в этой точке u =1. Так и в школе учили. Если выбрать две точки на большой окружности - сечении сферы плоскостью x =0, то плоскость, проходящая через полученную тройку точек совпадает с плоскостью x =0. Разумеется, предел такого семейства плоскостей при любом разумном понимании предела есть плоскость x =0. Если заменить плоскость x =0 на y =0, то претендентом на право именоваться касательной плоскостью станет и эта плоскость. Такой подход к определению касательной плоскости оказался несостоятельным! А второй подход к определению касательной к кривой оказывается эффективным. Определение 12. Плоскость P называется касательной плоскостью к поверхности u = f (x, y) в точке N 0(x 0, y 0, u 0), если - плоскость проходит через точку N 0, -
Рис. 2 Теорема 10. Если функция f (x, y) дифференцируема в точке M 0(x 0, y 0), то касательная плоскость существует и ее уравнение имеет вид
Доказательство. Пусть x - x 0=D x, y - y 0=D y, f (x, y)- f (x 0, y 0)=D u.
В последнем неравенстве использовано неравенство | n | ³1. Здесь в числителях абсолютная величина числа, в знаменателях модуль вектора - обозначения совпадают. По определению дифференцируемости числитель последней дроби есть o(r), где
Нормалью к поверхности называется прямая, ортогональная к касательной плоскости. Из аналитической геометрии известно, что нормаль задается уравнениями
Пример. Рассмотрим сферу x 2+ y 2+ u 2=1 и точку на поверхности (0,0,1). Верхняя полусфера задается уравнением
В точке (0,0) обе частные производные обращаются в 0. Подставляя их в уравнение касательной плоскости, получаем уравнение u =1 - оно совпало с нашими представлениями. Следует иметь в виду, что так нельзя было бы действовать при нахождении касательной плоскости к сфере в точке (1,0,0) - частные производные функции u = f (x, y) в точке (1,0) не существуют. При этом на сфере все точки равноправны. В этом случае надо вместо u использовать другую переменную (x). К этому вопросу мы еще вернемся. Отметим следующее обстоятельство. Если рассечь поверхность плоскостью, проходящей через точку N 0, параллельной вектору n, то в сечении получим плоскую кривую, касательная к которой ортогональна n, а значит лежит в касательной плоскости - вполне естественное свойство. На самом деле это справедливо для любой гладкой кривой, проходящей на поверхности через точку N 0. Разумеется, для этого надо определять касательную к кривой в первоначальном смысле через угол между секущей и касательной - нормаль к пространственной кривой определяется неоднозначно.
Вопросы для самопроверки 1. Какие подходы существуют к определению касательной к кривой? 2. Как корректно определить касательную плоскость к поверхности? 3. Как выглядит уравнение касательной плоскости к графику дифференцируемой функции двух переменных?
Упражнение 1. Записать уравнения касательных плоскостей и нормалей к заданным поверхностям в данных точках - -
|
||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 77; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.110.169 (0.008 с.) |
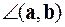 угол между векторами, если он не превосходит p/2 или дополнение до p угла между векторами, если это не так.
угол между векторами, если он не превосходит p/2 или дополнение до p угла между векторами, если это не так.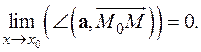
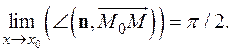 Это условие можно сформулировать так:
Это условие можно сформулировать так: 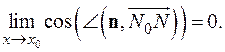 Условие в такой форме удобнее, поскольку векторная алгебра дает простой способ вычисления косинуса угла между ненулевыми векторами. Правда, годится такой подход только для плоских кривых.
Условие в такой форме удобнее, поскольку векторная алгебра дает простой способ вычисления косинуса угла между ненулевыми векторами. Правда, годится такой подход только для плоских кривых.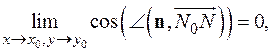 где N - точка (x, y, u), u = f (x, y), n - нормальный вектор плоскости P (рис. 2).
где N - точка (x, y, u), u = f (x, y), n - нормальный вектор плоскости P (рис. 2).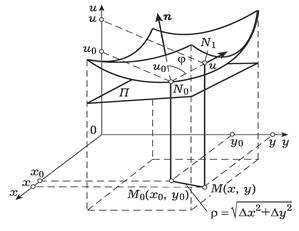
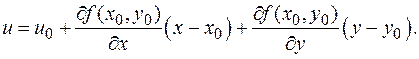
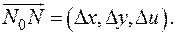 Нормальный вектор плоскости из формулировки теоремы имеет координаты
Нормальный вектор плоскости из формулировки теоремы имеет координаты 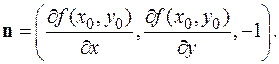 Тогда
Тогда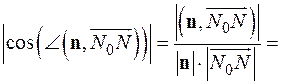
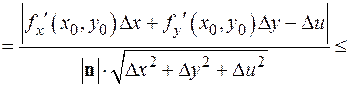
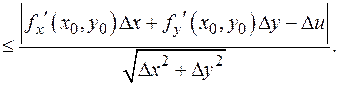
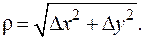 Отсюда,
Отсюда, 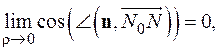 что и требовалось доказать.
что и требовалось доказать.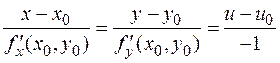 .
.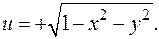 Вычислим частные производные:
Вычислим частные производные: