
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несинусоидальные токи и напряжения.Содержание книги
Поиск на нашем сайте
Основные понятия, причины возникновения несинусоидальных напряжений и токов.
Синусоидальные колебания являются самой простой формой периодического процесса. В сетях электроэнергетических систем принимается ряд мер для поддержания синусоидальной формы переменных токов и напряжений и устранения различных отклонений от синусоидальной формы. Но, например, в цепях электросвязи, электронных и полупроводниковых устройств отклонение от синусоидальной формы часто обусловлено самим рабочим процессом устройства. Поэтому знание элементов теории несинусоидальных периодических токов необходимо для понимания принципов действия устройств автоматики, электронных приборов и самой различной аппаратуры новой техники. Периодическая несинусоидальная функция удовлетворяет условию Такая периодическая функция, как известно из курса математики, может быть представлена в виде гармонического ряда (ряда Фурье), в общем случае неограниченного, но при расчетах электрических цепей часто с конечным числом п гармонических (синусоидальных) составляющих или, короче, гармоник. Например, не синусоидальный периодический ток
или
В этом выражении
Рис. 1 На рис. 1 приведен график периодического несинусоидального тока
ЭДС источников:
и других величин. Выражение (1) можно преобразовать, применив известную из тригонометрии формулу синуса суммы двух углов:
Обозначив постоянные величины
получим
Применяя подобную запись ко всем гармоническим составляющим, несинусоидальную функцию можно выразить так:
Особенность такой записи состоит в том, что гармоники составляют рад синусов и ряд косинусов с нулевыми начальными фазами. Обратный переход от ряда (2) к ряду (1) нетрудно сделать, определив
При определении угла При построении синусоид по оси абсцисс нужно откладывать начальную фазу k-ой гармоники, пересчитав ее на масштаб основной гармоники, т.е. вместо Это следует из того, что градуировка оси абсцисс дается в масштабе первой гармоники, поэтому на отрезке Коэффициенты
Если закон изменения ординат несинусоидальной кривой можно выразить в виде уравнения, то выражения (4) – (6) позволяют в большинстве случаев выполнить аналитически разложение ее в тригонометрический ряд вида (2) и далее, если нужно, перейти к ряду (1). Постоянная составляющая, как видно из формулы (4), является средним значением функции за ее период. Таким образом, постоянная составляющая в тригонометрическом ряду отсутствует, если среднее за период значение функции равно нулю. Для расчета режима линейной цепи периодического не синусоидального тока (цепи, у которой параметры элементов r, L, С не зависят от тока и напряжения) применим метод наложения (см. § 1.12): каждую из гармонических составляющих и постоянную составляющую (если она есть) определим отдельно (независимо).
Рис. 2 В качестве примера рассмотрим расчет тока в цепи по рис. 2 при заданном напряжении источника периодической несинусоидальной ЭДС:
Ток в этой цепи
где по закону Ома для первой гармоники для пятой гармоники При определении каждой из гармонических составляющих можно применять любые методы расчета цепей синусоидального тока, в том числе и комплексный. Мгновенные значения токов и других величин можно рассчитать, как было отмечено выше, с применением метода наложения. Но практически весьма важно вычислить и действующие значения токов (напряжений, ЭДС), измеряемых амперметрами (вольтметрами). Приведенное ранее определение действующего значения на основании сопоставления с тепловым действием постоянного тока справедливо для любого периодического тока. Поэтому действующее значение периодического несинусоидального тока определим выражением
Учитывая (1а), интеграл 1) так как этот интеграл по определению равен квадрату действующего значения 2) 3) 4) Таким образом, действующее значение периодического несинусоидального тока
или
т. е. действующее значение периодического несинусоидального тока равно корню квадратному из суммы квадратов постоянной составляющей и квадратов действующих значений всех гармонических составляющих. Так же определяется действующее значение периодического несинусоидального напряжения:
и аналогично любой другой периодической несинусоидальной величины. Несинусоидальные периодические кривые характеризуются коэффициентом амплитуды, коэффициентом формы, а также коэффициентом искажения d. Коэффициент искажения равен отношению действующих значений основной гармоники и всей функции
Для синусоиды d = 1. Выражение мгновенной мощности
справедливо для токов и напряжений с любой формой кривой. Активная мощность любого периодического тока по определению равна среднему за период значению мгновенной мощности:
После подстановки в (11) напряжения u [см. (2) ] и тока i [см. (1)] в виде рядов активная мощность будет представлена суммой интегралов таких же четырех типов, которые были рассмотрены при определении действующего значения периодического несинусоидального тока: 1) 2) 3)
4) Таким образом, активная мощность
т. е. активная мощность периодического несинусоидального тока равна сумме активных мощностей всех гармонических составляющих и мощности постоянных составляющих напряжения и тока (мощности постоянного тока). Реактивной мощностью периодических несинусоидальных токов можно условно считать величину
Полная мощность периодического несинусоидального тока определяется также условно:
Метод расчета электрической цепи с несинусоидальным напряжением на входе.
Цели и задачи расчета электрических цепей с несинусоидальными токами не отличается от тех, которые были указаны для цепей постоянного тока и цепей с синусоидальными напряжениями и токами.
|
||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.47.139 (0.008 с.) |

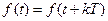 , где Т - период функции, т. е. промежуток времени, по истечении которого весь процесс повторяется сначала; k - целое число.
, где Т - период функции, т. е. промежуток времени, по истечении которого весь процесс повторяется сначала; k - целое число.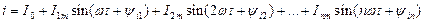 , (1)
, (1)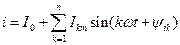 . (1а)
. (1а)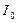 - постоянная составляющая (постоянный ток);
- постоянная составляющая (постоянный ток); 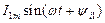 - первая (основная) гармоника, частота которой равна частоте несинусоидальной периодической функции - тока
- первая (основная) гармоника, частота которой равна частоте несинусоидальной периодической функции - тока 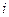 ; все остальные слагаемые называют высшими гармониками;
; все остальные слагаемые называют высшими гармониками; 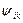 — начальная фаза k-ой гармонической составляющей, зависящая от начала отсчета времени (t = 0). Таким образом, периодический несинусоидальный ток можно представить в виде суммы постоянного тока и синусоидальных токов различных частот, кратных частоте первой гармоники, с различными начальными фазами. Такое представление часто применяется при расчетах цепей периодических несинусоидальных токов.
— начальная фаза k-ой гармонической составляющей, зависящая от начала отсчета времени (t = 0). Таким образом, периодический несинусоидальный ток можно представить в виде суммы постоянного тока и синусоидальных токов различных частот, кратных частоте первой гармоники, с различными начальными фазами. Такое представление часто применяется при расчетах цепей периодических несинусоидальных токов.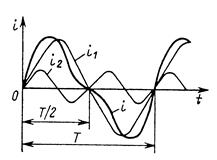
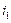 и вторую
и вторую 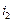 гармоники. Аналогично (1а) записываются разложения в гармонический ряд периодических не синусоидальных напряжений на любом участке цепи:
гармоники. Аналогично (1а) записываются разложения в гармонический ряд периодических не синусоидальных напряжений на любом участке цепи: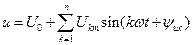 ,
,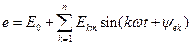
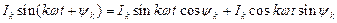 .
.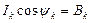 ,
, 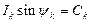 ,
,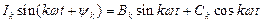 .
.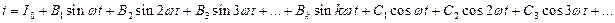
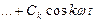 . (2)
. (2)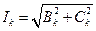 и
и 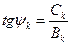 . (3)
. (3)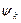 нужно учитывать порознь знаки
нужно учитывать порознь знаки 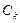 и
и 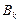 , так как от них зависит величина угла. Например, при положительных
, так как от них зависит величина угла. Например, при положительных 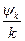 .
.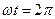 укладывается k полных циклов k-ой гармоники.
укладывается k полных циклов k-ой гармоники.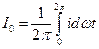 ; (4)
; (4)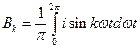 ; (5)
; (5)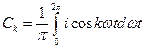 . (6)
. (6)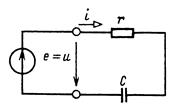
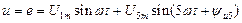 .
.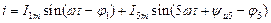 ,
,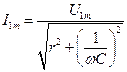 ,
,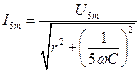 , а
, а 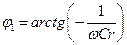 и
и 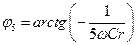 .
.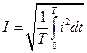 . (7)
. (7)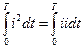 можно представить в виде суммы интегралов четырех типов:
можно представить в виде суммы интегралов четырех типов: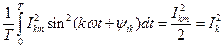 ,
,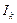 гармонической составляющей тока k-го порядка.
гармонической составляющей тока k-го порядка. - это квадрат постоянной составляющей тока;
- это квадрат постоянной составляющей тока;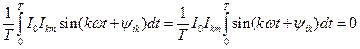 , так как интеграл от синусоидальной величины за целое число периодов равен нулю;
, так как интеграл от синусоидальной величины за целое число периодов равен нулю;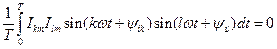 , где k и l - номера гармоник, причем к
, где k и l - номера гармоник, причем к 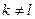 ; интеграл равен нулю, так как произведение синусоидальных функций можно заменить разностью косинусоидальных:
; интеграл равен нулю, так как произведение синусоидальных функций можно заменить разностью косинусоидальных:  , т. е. подынтегральное выражение интеграла 4-го типа является разностью двух косинусоидальных функций, интеграл каждой из которых за целое число периодов равен нулю.
, т. е. подынтегральное выражение интеграла 4-го типа является разностью двух косинусоидальных функций, интеграл каждой из которых за целое число периодов равен нулю.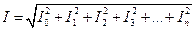 ,
,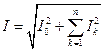 , (8)
, (8)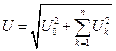 (9)
(9)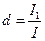 . (10)
. (10)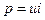 (11)
(11)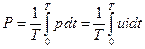 . (12)
. (12)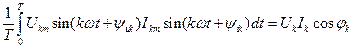 , где
, где 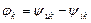 .
. ;
;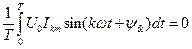 ;
;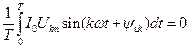 ;
;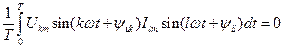 при
при 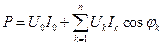 , (13)
, (13)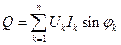 . (14)
. (14)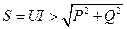 .
.


