
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Символический метод расчета электрических цепей переменного тока.
Выражение электрических величин комплексными числами. Законы Ома, Кирхгофа в символической форме.
Проведем на комплексной плоскости (рис. 4.21) из начала координат под углом
Рис. 4.21 При увеличении во времени фазы синусоидальной величины
При представлении синусоидальных величин комплексными числами можно применить эффективный комплексный метод анализа электрических цепей, который в настоящее время завоевал всеобщее признание. Вектор на комплексной плоскости, длина которого в масштабе построения равна действующему значению синусоидальной величины, и соответствующее комплексное число называются комплексным действующим значением синусоидальной величины:
Из курса математики известно, что каждому вектору · алгебраической - · тригонометрической - · показательной - При анализе цепей синусоидального тока применяют комплексные дейстыующие значения синусоидальных величин. Сокращенно их называют комплексными значениями, а соответствующие векторы на комплексной плоскости – векторами комплексных значений. Совокупность векторов комплексных значений синусоидальных величин одной частоты называется векторной диаграммой. Пользуясь векторной диаграммой, сложение и вычитание комплексных значений можно заменить сложением и вычитанием соответствующих векторов. Это упрощает расчеты и делает их наглядными. Взаимное расположение векторов комплексных значений на векторной диаграмме не изменится, если начальные фазы
Направления синусоидальных величин (тока, напряжения и др.) в цепи периодически изменяются, но одно из двух направлений принимается положительным. Это направление выбирается произвольно и показывается стрелкой на схеме соответствующего участка цепи. При выбранном положительном направлении синусоидальная величина представляется мгновенным значением
Рис. 4.22 Зависимость между токами и напряжениями резистивных, емкостных и индуктивных элементов определяются происходящими в них физическими процессами. Математическое описание физических процессов в каждом из этих элементов зависит от выбранного способа представления синусоидальных величин. Сопротивление. Если ток в цепи с резистором синусоидальный
где амплитуда тока и напряжения и их начальные фазы связаны соотношениями
Разделив обе части соотношения (127) на
Рис. 4.23 На рис. 4.23 показан график мгновенных значений синусоидальных тока и напряжения резистора, из которого видно, что синусоидальный ток и напряжение совпадают по фазе. Представим ток и напряжение соответствующими комплексными значениями:
Учитывая (128), получим закон Ома в комплексной форме для резистора:
или
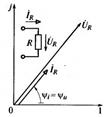
Рис. 4.24 На рис. 4.24 приведена векторная диаграмма резистора и показано, что векторы комплексных значений тока и напряжения совпадают по фазе. Индуктивный элемент. Если ток в катушке синусоидальный, то по закону электромагнитной индукции напряжение на концах катушки
где амплитуды напряжения и тока и их начальные фазы связаны соотношениями
Разделив обе части соотношения (130) на
Величина
Рис. 4.25 На рис. 4.25 показан график мгновенных значений синусоидальных тока и напряжения катушки, из которого видно, что синусоидальный ток отстает по фазе от синусоидального напряжения на угол Представим ток и напряжение соответствующими комплексными значениями:
На рис. 4.26 приведена векторная диаграмма катушки и показано, что вектор комплексного значения тока отстает по фазе от вектора комплексного значения напряжения на угол
или
Рис. 4.26 Величина Емкостной элемент. Если напряжение между выводами конденсатора изменяется синусоидально, то ток в емкостном элементе
где амплитуды напряжения и тока и их начальные фазы связаны соотношениями
Разделив обе части соотношения (133) на
Величина В противоположность индуктивному сопротивлению емкостное сопротивление уменьшается с увеличением частоты синусоидального тока и при постоянном напряжении бесконечно велико.
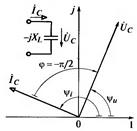
Рис. 4.27 На рис. 4.27 показан график мгновенных значений синусоидальных тока и напряжения конденсатора, из которого видно, что синусоидальное напряжение отстает по фазе от синусоидального тока на угол Представим ток и напряжение соответствующими комплексными значениями:
Рис. 4.28 На рис. 4.28 приведена векторная диаграмма емкостного элемента и показано, что вектор комплексного значения напряженя отстает по фазе от вектора комплексного значения тока на угол Пользуясь соотношениями (133) и (134), получим закон Ома в комплексной форме для емкостного элемента:
или
Величина Первый закон Кирхгофа. По первому закону Кирхгофа алгебраическая сумма токов в любом узле электрической цепи в каждый момент времени равна нулю:
где n – число ветвей, сходящихся в узле; k – порядковый номер ветви. В дальнейшем все синусоидальные токи, положительные направления которых выбраны к узлу (от узла), будем записывать со знаком минус (плюс). Например, для узла на рис. 4.29 и мгновенных значений синусоидальных токов
по первому закону Кирхгофа для любого момента времени
Представив все синусоидальные токи в (136) соответствующими им комплексными значениями, получим первый закон Кирхгофа в комплексной форме:
т.е. алгебраическая сумма комплексных значений токов в любом узле цепи синусоидального тока равна нулю. Здесь комплексные значения токов, для которых положительные направления выбраны к узлу (от узла), записываются со знаком минус (плюс).
Рис. 4.29 Второй закон Кирхгофа. По второму закону Кирхгофа алгебраическая сумма напряжений всех участков любого контура электрической цепи в каждый момент времени равна нулю:
где напряжения, положительные направления которых совпадают (противоположны) с произвольно выбранным направлением обхода контура, записываются со знаком плюс (минус); m – число участков; k – порядковый номер участка. Для контура схемы цепи, содержащего только пассивные элементы (резисторы, катушки, конденсаторы) и источники ЭДС, в каждый момент времени алгебраическая сумма напряжений на пассивных элементах контура равна алгебраической сумме ЭДС, т.е. второй закон Кирхгофа принимает вид
где n и m - числа пассивныз элементов и источников ЭДС в контуре. В выражении (137) напряжения и ЭДС, для которых положительные направления совпадают (противоположны) с произвольно выбранным направлением обхода контура, записываются со знаком плюс (минус).
Расчет электрических цепей символическим методом. Векторные диаграммы.
Комплексный метод расчета цепи синусоидального тока заключается в следующем. 1. Представляем исходные данные о параметрах всех элементов цепи в комплексной форме, т.е. синусоидальные ЭДС источников напряжений и токи источников тока, заданных мгновенными значениями (в тригонометрической форме), индуктивные и емкостные элементы цепи соответствующими им комплексными значениями и комплексными сопротивлениями или проводимостями (см. таблицы).
2. Выбираем положительные направления комплексных токов во всех ветвях и указываем их стрелками на схеме цепи. 3. По законам Ома и Кирхгофа в комплексной форме составляем систему уравнений, определяющую режим работы цепи. 4. Решаем полученную систему уравнений и определяем комплексные значения токов в ветвях цепей и напряжений на ее элементах. 5. По найденным комплексным значениям токов и напряжений определяем соответствующие им мгновенные значения синусоидальных токов и напряжений. Для упрощения вычислений при расчете линейных цепей синусоидального тока, так же как и линейных цепей постоянного тока, применимы различные расчетные методы: преобразования схем, узловых потенциалов, контурных токов, наложения.
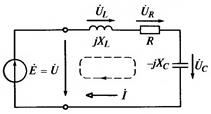
При этом математические формулировки методов расчета цепей синусоидального тока. Нужно только все ЭДС, напряжения и токи заменить комплексными значениями соответствующих синусоидальных величин, в сопротивления элементов – комплексными сопротивлениями. Рассмотрим общий, а затем – частные случаи цепи с последовательным соединением элементов, т.е. неразветвленные цепи. Цепь с последовательным соединением элементов R, L, C (рис. 4.30).
Рис. 4.30 В данной цепи при действии источника с синусоидальной ЭДС ток также синусоидальный и напряжения на резисторе, катушке и конденсаторе равны
Для расчета режима работы цепи комплексным методом представим все синусоидальные величины соответствующими комплексными величинами по (126)
На рис. 4.30 стрелками показаны положительные направления тока, ЭДС и напряжений. Выберем направление обхода контура и запишем уравнение по второму закону Кирхгофа (137):
Здесь учтен закон Ома для всех трех элементов цепи в комплексной форме. Из (138) найдем комплексный ток в цепи
или
где Величина, стоящая в знаменателе формулы (139), называется комплексным сопротивлением неразветвленного участка цепи:
Величина, обратная комплексному сопротивлению, называется комплексной проводимостью:
Обозначения комплексных сопротивлений и проводимости отличаются от обозначений комплексных значений тока и напряжения потому, что вторым соответствуют физические величины, изменяющиеся во времени, а первым – нет. Каждому значению комплексного сопротивления
Рис. 4.31 Этот вектор является геометрической интерпретацией комплексного сопротивления и имеет такое же обозначение
где В зависимости от знака величины Подставив значение комплексного сопротивления в показательной форме в (139), получим выражение закона Ома для неразветвленной цепи:
или
где
При известном комплексном токе в цепи комплексные напряжения на резисторе, катушке и конденсаторе рассчитываются по соответствующим формулам. На рис. 4.32 приведены векторные диаграммы тока и напряжения неразветвленной цепи (см. рис. 4.30) для двух случаев:
Рис. 4.32 Если комплексное сопротивление цепи имеет индуктивный характер, то ток в цепи отстает по фазе от напряжения, так как угол Цепь с последовательным соединением элементов R и L (рис. 4.33). В цепи с последовательным соединением резистора и катушки (рис. 4.33 а) выражения (138) и (140) принимают вид
которым соответствуют на векторных диаграммах прямоугольные треугольники напряжений и сопротивлений (рис. 4.33 б и в). Из прямоугольных треугольников напряжений и сопротивлений следует, что полное сопротивление цепи равно
а приложенное к ней напряжение и ток в цепи равны
Рис. 4.33 Цепь с последовательным соединением элементов R и С (рис. 4.34). В цепи с последовательным соединением резистора и конденсатора (рис. 4.34 а) выражения (138) и (140) принимают вид
которым соответствуют на векторных диаграммах прямоугольные треугольники напряжений и сопротивлений (рис. 4.34 б и в). Из прямоугольных треугольников напряжений и сопротивлений следует, что полное сопротивление цепи равно
а приложенное к ней напряжение и ток в цепи равны
Рис. 4.34
Электрические цепи с взаимной индукцией.
Рассмотрим особенности расчета цепей, в которых есть индуктивно связанные катушки. Начнем в простейшей цепи, состоящей из двух последовательно соединенных катушек, представленных последовательными схемами замещения. В этом случае возможно их согласное или встречное включение. При согласном включении (рис. 4.35 а) магнитный поток первой катушки Ф11 и часть магнитного потока второй катушки, пронизывающего первую Ф21, суммируются. Также суммируются потоки Ф22 и Ф12, суммируются и возбуждаемые ими ЭДС индукции и взаимной индукции, соответственно равны
и
где при последовательном соединении
Рис. 4.35 Напряжение u1 на выводах первой катушки при согласном соединении состоит из трех слагающих:
или в комплексной форме
Уравнение (146) записано так же, как и уравнение по второму закону Кирхгофа в комплексной форме, только слева вместо ЭДС источника питания стоит напряжение на выводах (т.е. напряжение питания цепи из двух последовательно соединенных катушек), а справа дополнительно учтено падение напряжения, компенсирующее ЭДС взаимной индукции. Аналогично напряжение на выводах второй катушки
или в комплексной форме
Напряжение на выводах цепи
или
Векторная диаграмма цепи при последовательном согласном включении двух катушек показана на рис. 4.35 б. Для того, чтобы отличить на схемах согласное включение от встречного, один из выводов катушек называют началом, а другой – концом. У одной из катушек начало и конец могут быть выбраны произвольно. У второй катушки началом называется тот вывод, который надо присоединить к концу первой, чтобы получилось согласное соединение. Т.е. при согласном включении катушки соединены друг с другом разноименными выводами. Начало катушек отмечается каким-либо знаком, например точкой (рис. 4.35 а), звездочкой и т.д. При встречном включении катушек ЭДС самоиндукции и взаимной индукции вычитаются. Поэтому напряжение на выводах первой катушки
или
Аналогично
и
Рис. 4.36 Встречное включение получается, если катушки соединены друг с другом одноименными выводами (рис. 4.36 а). На рис. 4.36 б дана векторная диаграмма цепи при встречном включении катушек. Суммарная (эквивалентная) индуктивность цепи и ее индуктивное сопротивление при согласном включении (148) больше, чем при встречном (151). При согласном соединении
и
при встречном соединении
и
В качестве примера параллельного соединения катушек рассмотрим воздушный трансформатор (рис. 4.37).
Рис. 4.37 Обмотка трансформатора, присоединяемая к источнику питания с напряжением Положительные направления напряжения
Таким образом, напряжение
Рис. 4.38 Так как во вторичной цепи нет источника питания, то можно по второму закону Кирхгофа записать
где ЭДС взаимной индукции во вторичной обмотке согласно (145)
или из (155)
На диаграмме (рис. 4.38) показано, что ЭДС Из (156) определяется ток вторичной цепи
Подставив это выражение тока
где Второе слагаемое входного сопротивления называется вносимым сопротивлением в первичную цепь:
и учитывая влияние вторичной цепи с сопротивлением Для источника питания нагруженный трансформатор можно представить простой схемой замещения (рис. 4.39). Действительно, по закону Ома
что совпадает с (157). Из (157) определяется ток
после чего ток
Рис. 4.39 Итак, при заданных параметрах первичной и вторичной цепей и напряжении источника питания можно рассчитать токи В частном случае ненагруженного трансформатора, т.е. в режиме холостого хода,
Возможны два случая параллельного соединения катушек: одноименными и разноименными выводами к общему узлу.
Рис. 4.40 На рис. 4.40 а показано присоединение катушек одноименными выводами – началами к общему верхнему узлу. Выбрав положительные направления токов так, как показано на рис. 4.40 а, будем считать такое соединение согласным (точки входят в одноименные выводы). Напряжение на первой ветви
Напряжение на второй ветви
где Исключая из (161) и (162) ток
Аналогично, исключая ток
Уравнения для напряжения Естественно, что ток в неразветвленной части цепи для любой из параллельных схем соединения катушек определяется по одной и той же формуле:
На рис. 4.40 б показана векторная диаграмма для цепи при параллельном соединении катушек по рис. 4.40 а.
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 172; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.32.86 (0.162 с.) |
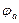 у оси действительных величин против часовой (по часовой) стрелки, если значение угла
у оси действительных величин против часовой (по часовой) стрелки, если значение угла  (
( ) вектор, длина которого в масштабе построения равна амплитуде
) вектор, длина которого в масштабе построения равна амплитуде 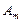 синусоидальной величины. Конец этого вектора находится в точке, которой соответствует комплексное число
синусоидальной величины. Конец этого вектора находится в точке, которой соответствует комплексное число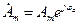 .
.
 угол между осью и вектором растет, а сам вектор будет представлять собой вращающийся вектор
угол между осью и вектором растет, а сам вектор будет представлять собой вращающийся вектор .
. . (126)
. (126)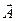 в комплексной плоскости (рис. 4.21) соответствует комплексное число
в комплексной плоскости (рис. 4.21) соответствует комплексное число 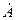 , которое можно выразить в форме:
, которое можно выразить в форме: ;
;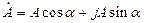 ;
;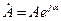 .
. .
. и соответствующим комплексным значением
и соответствующим комплексным значением 
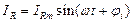 , то по закону Ома напряжение на резисторе
, то по закону Ома напряжение на резисторе ,
,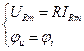 . (127)
. (127) , получим соотношение для действующих значений напряжения и тока в резисторе:
, получим соотношение для действующих значений напряжения и тока в резисторе: . (128)
. (128)
 и
и 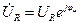 .
. , (129)
, (129) .
.
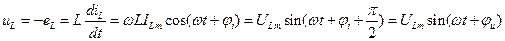 ,
, . (130)
. (130) . (131)
. (131) называется индуктивным сопротивлением, а обратная ей величина
называется индуктивным сопротивлением, а обратная ей величина  - индуктивной проводимостью. Величины
- индуктивной проводимостью. Величины  и
и  - параметры индуктивных элементов цепей синусоидального тока.
- параметры индуктивных элементов цепей синусоидального тока.
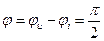 .
. и
и 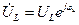 .
.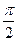 . Пользуясь соотношениями (130) и (131), получим закон Ома в комплексной форме для индуктивного элемента:
. Пользуясь соотношениями (130) и (131), получим закон Ома в комплексной форме для индуктивного элемента: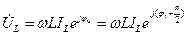 ,
, . (132)
. (132)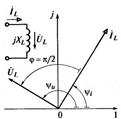
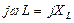 называется комплексным индуктивным сопротивлением, а обратная ей величина
называется комплексным индуктивным сопротивлением, а обратная ей величина  - комплексной индуктивной проводимостью.
- комплексной индуктивной проводимостью. ,
,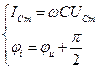 . (133)
. (133) . (134)
. (134) называется емкостным сопротивлением, а обратная ей величина
называется емкостным сопротивлением, а обратная ей величина  - емкостной проводимостью. Величины
- емкостной проводимостью. Величины 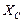 и
и 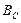 - параметры емкостных элементов цепей синусоидального тока.
- параметры емкостных элементов цепей синусоидального тока.
 , т.е. смещение по фазе между напряжением и током
, т.е. смещение по фазе между напряжением и током  .
.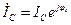 и
и 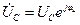 .
.
 ,
, . (135)
. (135) называется комплексным емкостным сопротивлением, а обратная ей величина
называется комплексным емкостным сопротивлением, а обратная ей величина 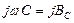 - комплексной емкостной проводимостью.
- комплексной емкостной проводимостью. , (136)
, (136) ;
;  ;
; 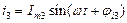
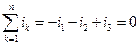 .
.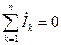 , (137)
, (137)
 , (136)
, (136) , (137)
, (137)

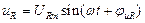 ;
; 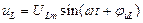 ;
; 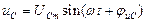 .
. ;
;  ;
; 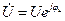 ;
;  ;
; 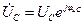 .
. . (138)
. (138)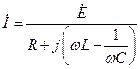 ,
,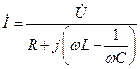 , (139)
, (139) - напряжение между выводами источника и пассивного участка.
- напряжение между выводами источника и пассивного участка. . (140)
. (140) .
. как комплексному числу соответствует точка на комплексной плоскости. Ее положение определяется вектором на комплексной плоскости (рис. 4.31).
как комплексному числу соответствует точка на комплексной плоскости. Ее положение определяется вектором на комплексной плоскости (рис. 4.31).
 (рис. 4.31 а) и
(рис. 4.31 а) и  (рис. 4.31 б). Геометрическая интерпретация комплексного сопротивления позволяет легко перейти от алгебраической формы записи комплексного сопротивления к тригонометрической и показательной формам
(рис. 4.31 б). Геометрическая интерпретация комплексного сопротивления позволяет легко перейти от алгебраической формы записи комплексного сопротивления к тригонометрической и показательной формам , (141)
, (141) - модуль комплексного сопротивления, или полное сопротивление,
- модуль комплексного сопротивления, или полное сопротивление, 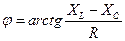 - аргумент комплексного сопротивления.
- аргумент комплексного сопротивления. аргумент комплексного сопротивления может быть либо положительным (
аргумент комплексного сопротивления может быть либо положительным ( - индуктивный характер комплексного сопротивления, как на рис. 4.31 а), либо отрицательным (
- индуктивный характер комплексного сопротивления, как на рис. 4.31 а), либо отрицательным ( - емкостной характер комплексного сопротивления, как на рис. 4.31 б), но всегда
- емкостной характер комплексного сопротивления, как на рис. 4.31 б), но всегда 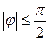 .
. ,
, , (142)
, (142) - действующее значение тока;
- действующее значение тока; 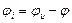 - начальная фаза тока.
- начальная фаза тока.
 . Если комплексное сопротивление цепи имеет емкостной характер, то ток в цепи опережает по фазе напряжение, так как угол
. Если комплексное сопротивление цепи имеет емкостной характер, то ток в цепи опережает по фазе напряжение, так как угол  . На векторной диаграмме положительное (отрицательное) значение угла
. На векторной диаграмме положительное (отрицательное) значение угла  отсчитывает против направления (по направлению) движения часовой стрелки от вектора комплексного значения тока
отсчитывает против направления (по направлению) движения часовой стрелки от вектора комплексного значения тока  .
.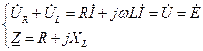 , (143)
, (143) ,
, ;
; 
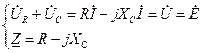 , (143)
, (143) ,
, ;
; 
 ;
;  (144)
(144) ;
;  , (145)
, (145) .
.

 . (146)
. (146)
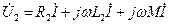 . (147)
. (147)
 . (148)
. (148)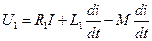
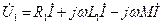 . (149)
. (149)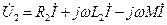 . (150)
. (150) . (151)
. (151)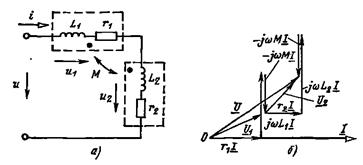
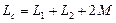 ,
, ; (152)
; (152) ,
,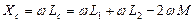 ; (153)
; (153)
 , называется первичной, другая, к которой подключается приемник, например, с активным сопротивлением R, называется вторичной.
, называется первичной, другая, к которой подключается приемник, например, с активным сопротивлением R, называется вторичной.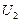 на вторичной обмотке и тока
на вторичной обмотке и тока 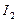 во вторичной цепи могут быть выбраны произвольно, например так, чтобы токи входили в одноименные выводы (рис. 4.37). В этом случае, как и при последовательном соединении, надо считать, что ЭДС самоиндукции и взаимной индукции суммируются и компенсирующие их напряжения записываются в уравнениях с одинаковыми знаками. Следовательно, напряжение на выводах первичной обмотки записывается аналогично (146):
во вторичной цепи могут быть выбраны произвольно, например так, чтобы токи входили в одноименные выводы (рис. 4.37). В этом случае, как и при последовательном соединении, надо считать, что ЭДС самоиндукции и взаимной индукции суммируются и компенсирующие их напряжения записываются в уравнениях с одинаковыми знаками. Следовательно, напряжение на выводах первичной обмотки записывается аналогично (146):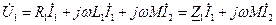 . (154)
. (154)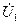 состоит из активной составляющей
состоит из активной составляющей 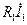 , совпадающей по фазе с током
, совпадающей по фазе с током  (рис. 4.38), составляющей
(рис. 4.38), составляющей  , опережающей по фазе ток
, опережающей по фазе ток  , опережающей по фазе ток
, опережающей по фазе ток  на 90°.
на 90°.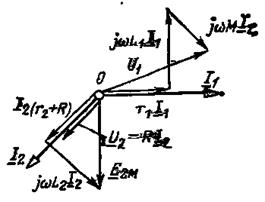
 , (155)
, (155) - напряжение на приемнике и оно же (рис. 4.37) на выводах вторичной обмотки;
- напряжение на приемнике и оно же (рис. 4.37) на выводах вторичной обмотки; 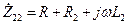 - сопротивление вторичной цепи.
- сопротивление вторичной цепи. ,
,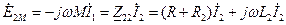 . (156)
. (156)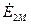 отстает по фазе от тока
отстает по фазе от тока  и
и  и на индуктивности
и на индуктивности  .
. .
. . (157)
. (157) - входное сопротивление наружного трансформатора.
- входное сопротивление наружного трансформатора.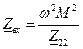 (158)
(158) на ток
на ток 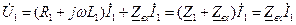 ,
, , (159)
, (159)
 и по (155) напряжение на вторичной обмотке
и по (155) напряжение на вторичной обмотке . (160)
. (160)
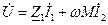 . (161)
. (161)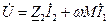 , (162)
, (162) и
и 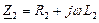 .
. . (163)
. (163) . (164)
. (164) при встречном соединении катушек отличаются от написанных для согласного соединения только знаком перед слагаемым с взаимной индуктивностью M.
при встречном соединении катушек отличаются от написанных для согласного соединения только знаком перед слагаемым с взаимной индуктивностью M.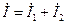 . (165)
. (165)


