Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соединение звездой трехпроводной.Содержание книги
Поиск на нашем сайте
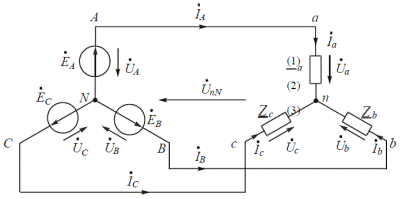
Схема замещения анализируемой цепи представлена на рис. 4.56.
Рис. 4.56 Приемник несимметричный. Трехфазные цепи являются разновидностью цепей синусоидального тока, поэтому для их расчета пригодны все методы, применяемые в однофазных цепях. Анализируемую схему можно рассматривать как схему с двумя узлами (N и n) и рассчитывать токи в ней методом напряжения между двумя узлами. Напряжение между нейтральными точками генератора и приемника можно вычислить по формуле
где Линейные и равные им соответственно фазные токи можно определить по закону Ома для активной ветви:
Выражения в скобках являются разностью потенциалов между началами (a,b,c) и концами (n) фаз приемников, то есть фазными напряжениями приемника. Например, Поэтому уравнения можно переписать в следующем виде:
На основании первого закона Кирхгофа геометрическая сумма токов
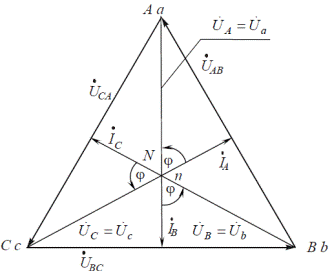
Уравнение Топографическую диаграмму строят в два этапа: 1. Построение топографической диаграммы напряжений генератора. 2. Построение топографической диаграммы напряжений приемника. Напряжение – разность потенциалов между двумя точками. Если известна картина распределения потенциалов различных точек схемы на комплексной плоскости, то, соединив две соответствующие точки, можно получить вектор нужного напряжения. Если сопротивлением линии пренебрегаем, то на схеме замещения начала фаз генератора и приемника коротко соединены между собой, тогда потенциалы их будут одинаковы. Точки А и a, B и b, C и c на комплексной плоскости совпадают. Между нейтральными точками генератора N и приемника n возникает напряжение Приемник симметричный. Если приемник симметричный (
Напряжение между нейтральными точками генератора и приемника не возникает. Напряжения генератора и приемника соответственно равны. Линейные и фазные токи равны по величине и сдвинуты по фазе относительно друг друга на угол
Рис. 4.57 Векторно-топографическая диаграмма для случая активной индуктивной нагрузки построена на рис. 4.57.
|
||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.199.54 (0.007 с.) |

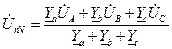 ,
,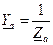 ,
, 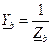 ,
, 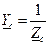 - комплексные проводимости фаз приемника.
- комплексные проводимости фаз приемника.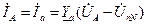 ;
; 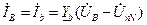 ;
; 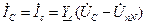 .
.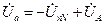 .
.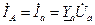 ;
; 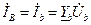 ;
; 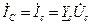 .
.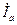 ,
, 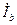 , и
, и 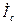 будет равна нулю.
будет равна нулю.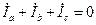 дает возможность проверить правильность решения.
дает возможность проверить правильность решения.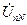 . Точка n на комплексной плоскости смещена относительно точки N. Поэтому напряжение
. Точка n на комплексной плоскости смещена относительно точки N. Поэтому напряжение 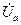 ,
, 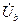 и
и 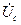 . Система фазных напряжений приемника несимметрична. Векторная диаграмма токов зависит от нагрузки.
. Система фазных напряжений приемника несимметрична. Векторная диаграмма токов зависит от нагрузки.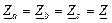 ,
, 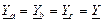 ), формула напряжения между двумя узлами может быть записана в виде
), формула напряжения между двумя узлами может быть записана в виде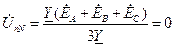 .
.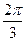 :
: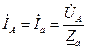 ;
; 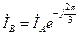 ;
; 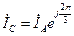 .
.