
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логические схемы и их таблицы истинности,Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Правила минимизации
Каноническая сумма минтермов
Минтерм – это полное произведение всех входных переменных, соответствующее одной строке таблицы истинности, в которой значение выходной переменной (значение функции) равно логической 1. Переменная входит в минтерм с инверсией, если ее значение в данной строке таблицы равно 0, и без инверсии, если ее значение в данной строке таблицы равно 1. Каноническая сумма минтермов – это логическая сумма всех минтермов, которая представляет собой максимальное логическое выражение, соответствующее таблице истинности. Она составляется в следующей последовательности: В заданной таблице истинности подсчитывается «n» – количество строк таблицы, в которой значение функции равно 1. Затем записывается логическая сумма «n» полных произведений. Далее в каждом произведении расставляются инверсии над переменными в соответствии с их значением в строке таблицы. Для примера, представленного на рисунке 3.8, каноническая сумма минтермов будет выглядеть так:
Рисунок 3.8 – Логическая схема и соответствующая ей таблица истинности Из сравнения (3.1) и (3.2) видно, что одной и той же таблице истинности (рисунок 3.8,б) соответствуют два разных логических выражения, причем (3.1) записывается более компактно, но возможности минимизации для него еще есть. Следовательно, есть возможность минимизировать и логическую схему, представленную на рисунке 3.8,a:
Минимизация логических выражений может осуществляться с помощью различных методов на основе правил булевой алгебры, в частности, диаграммы Вейча, диаграммы Венна и табличным методом, но наиболее простым и наглядным является графический способ минимизации с помощью карт Карно, опубликованный в 1953 г. Морисом Карно.
Правила минимизации логических схем с помощью карт Карно
Карта Карно – графическое представление таблицы истинности. Каждой клетке карты Карно соответствует строка таблицы истинности. По осям карты расставляются сочетания переменных, а внутри карты – значения функции. Назначение карты Карно – найти логические суммы прямого и инверсного значения переменных. Для любой переменной, например,
– сумму
|
||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 657; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.175 (0.01 с.) |

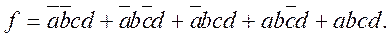 (3.2)
(3.2)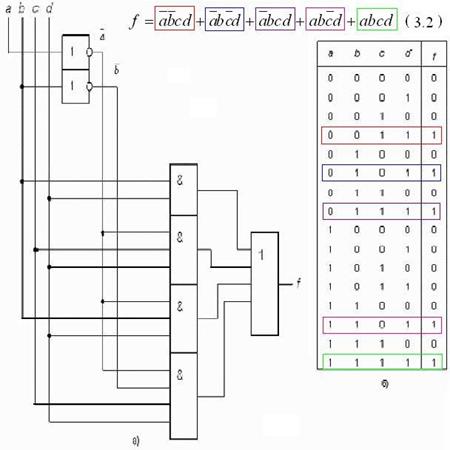
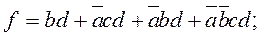
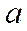 , такая сумма равна
, такая сумма равна 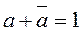 при любом значении
при любом значении 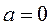 это будет 0+1=1, при
это будет 0+1=1, при 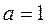 это 1+0=1. Поэтому при вынесении за скобки в выражении:
это 1+0=1. Поэтому при вынесении за скобки в выражении: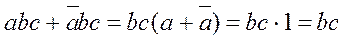
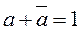 можно отбросить, при этом результат выражения не изменится. В этом и заключается минимизация логических выражений с помощью карт Карно. Для достижения поставленной цели минимизации нужно соблюдать правила разметки осей карты:
можно отбросить, при этом результат выражения не изменится. В этом и заключается минимизация логических выражений с помощью карт Карно. Для достижения поставленной цели минимизации нужно соблюдать правила разметки осей карты:


