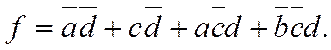Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные логические функции и элементы, их таблицы истинности, схемы и условно-графические обозначения.Содержание книги
Поиск на нашем сайте
Основные логические функции и элементы, их таблицы истинности, схемы и условно-графические обозначения. Основные законы и правила булевой алгебры логики. Логические схемы и их таблицы истинности, правила минимизации. 4. Основные термины и определения цифровой схемной логики.
Основные логические функции и элементы, их таблицы истинности, схемы и условно-графические обозначения
Уровни логических сигналов
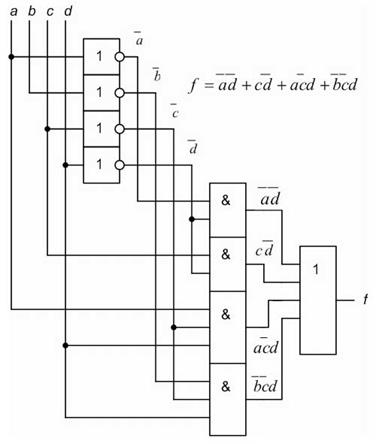
Любая цифровая вычислительная машина состоит из логических схем – таких схем, которые могут находиться только в одном из двух возможных состояний – либо "логический ноль ", либо "логическая единица". За логический 0 и логическую 1 можно принять любое выражение, в том числе и словесное, которое можно характеризовать как " истина " и " ложь ". В вычислительной технике логические 0 и 1 – это состояние электрических схем с определенными параметрами. Так, для логических элементов и схем, выполненных по технологии транзисторно-транзисторной логики (ТТЛ-схемы), логический 0 – это напряжение в диапазоне 0 + 0,4 В, а логическая 1 – это напряжение в диапазоне + 2,4…+5 В (рисунок 3.1). Работа логических схем описывается посредством специального математического аппарата, который называется логической (булевой) алгеброй или алгеброй логики. Булева алгебра была разработана Джорджем Булем (1815 – 1864 гг.), она является основой всех методов упрощения булевых выражений.
Рисунок 3.1 – Уровни логических сигналов на выходе цифровых ТТЛ-микросхем
Логические переменные и логические функции – это такие переменные и функции, которые могут принимать только два значения - либо логический 0, либо логическая 1.
Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1. В логических выражениях применяются обозначения: - либо - либо - либо - либо Логическая функция и элемент ИЛИ-НЕ
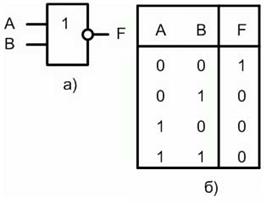
В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рисунке 3.6,а. Таблица истинности приведена на рисунке 3.6,б.
Рисунок 3.6 – Логический элемент ИЛИ-НЕ на два входа
Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0. В логических выражениях применяются обозначения: - либо - либо
Логические схемы и их таблицы истинности, Правила минимизации
Х переменных
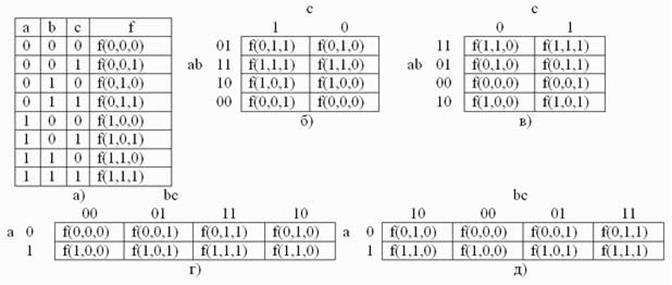
Рисунок 3.10 – Таблица истинности (а) и примеры заполнения карты Карно (б, в, г, д) для логической функции 3 переменных
Для функции четырех переменных карта Карно – это квадрат 4×4 клетки. В этих клетках размещаются 16 значений функции из последнего столбца таблицы истинности (рисунок 3.11). При разметке обеих осей нужно также четко придерживаться последнего, четвертого правила разметки и следить за тем, чтобы по одной оси соседними не оказались сочетания 00 и 11, либо 01 и 10, в которых одновременно меняются обе переменные. Для функции пяти переменных карта Карно представляет собой уже объемную фигуру – куб 4×4×4 клетки, поэтому для минимизации логических выражений она не применяется. В конкретных случаях вместо значений функций в общем виде в клетки карты проставляются конкретные значения (логические 0 и 1) из соответствующих строк таблицы истинности. Затем рассматриваются только те клетки, которые заполнены единицами. Все эти единицы должны быть обведены контурами по следующим правилам составления контуров: 1. Контуры должны быть прямоугольными и содержать количество единиц, равное 2 n, где n – целое число. Таким образом, в контуре может быть либо одна, либо две, либо четыре, либо восемь единиц. 2. Количество единиц в контуре должно быть максимальным, при этом контуры могут пересекаться между собой. Нужно учитывать, что крайние строки являются соседними и крайние столбцы также являются соседними, поэтому контуры могут быть " разорванными ". 3. Количество контуров должно быть минимальным, но все единицы должны быть охвачены контурами. Нельзя забывать об отдельно стоящих единицах. Каждая такая единица – это контур, которому соответствует полное логическое произведение всех переменных. 4. После обведения контуров нужно записать минимальное выражение как логическую сумму логических произведений. Каждому произведению соответствует один контур карты Карно. В произведение входят только те переменные, которые остаются в данном контуре неизменными. При этом переменная входит в произведение с инверсией, если ее значение в данном контуре равно 0, и без инверсии, если ее значение равно 1.
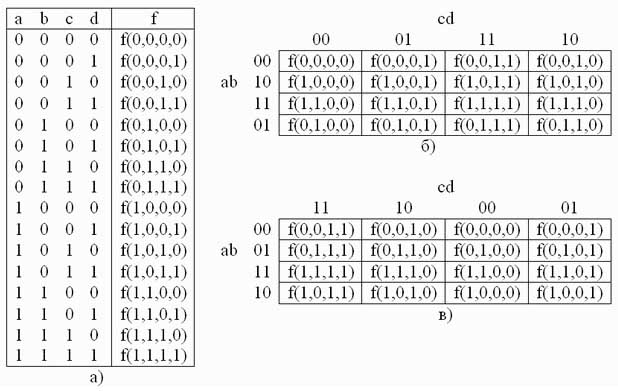
Рисунок 3.11 – Таблица истинности (а) и примеры заполнения карты Карно (б, в) для логической функции 4 переменных
Пример 1. Написать минимальное выражение для таблицы истинности, представленной на рисунке 3.12,а и нарисовать по нему логическую схему. При одном варианте разметки осей (рисунок 3.12,б) первый контур, состоящий из четырех единиц, получается разорванным. Если же принять разметку, показанную на рисунке 3.12в, то контур будет иметь нормальные очертания, а выражение, ему соответствующее, останется без изменений. Учитывая, что при данном горизонтальном начертании карты Карно крайние столбцы являются соседними, ее можно представить себе как цилиндр, развернутый на плоскости. На рисунке 3.12б представлена развертка такого цилиндра, "разрезанная" между комбинациями «bc», равными 10 и 11. А на рисунке 3.12в представлена развертка этого же цилиндра, "разрезанная" между произведениями «bc», равными 11 и 01. Первый контур охватывает четыре единицы, ему соответствует сумма минтермов:
Ему соответствует логическая схема на рисунке 3.12,г.
Рисунок 3.12 – Минимизация функции трех переменных
Для сравнения запишем максимальное выражение:
Разница между (3.3) и (3.4) очевидна и в комментариях не нуждается, за исключением того, что схема, реализованная по (3.4), будет на порядок сложнее и, соответственно, менее надежна, чем схема, показанная на рисунке 3.12,г. Пример 2. Написать минимальное выражение для таблицы истинности, представленной на рисунке 3.13,а, и нарисовать по нему логическую схему.
Рисунок 3.13 – Минимизация функции четырех переменных
При первоначально выбранной разметке осей (рисунок 3.13,б) первый контур, состоящий из четырех единиц с номерами 1.1, 1.2, 1.3 и 1.4, расположенных по углам карты, получается разорванным. Если же принять разметку, показанную на рисунке 3.14, то контур будет иметь очертания квадрата, а выражение, ему соответствующее, останется без изменений. Учитывая, что крайние столбцы являются соседними и крайние строки являются соседними, карту Карно для функции четырех переменных можно представить себе как торроид, развернутый на плоскости. Проще представить себе обратный процесс получения торроида из плоской фигуры – квадрата. Для этого надо сначала соединить мысленно крайние строки – получим цилиндр. После этого основания цилиндров надо мысленно соединить. Получится торроид. На рисунке 3.136 б представлена развертка такого торроида, "разрезанная" между комбинациями
Рисунок 3.14 – К минимизации логической функции четырех переменных
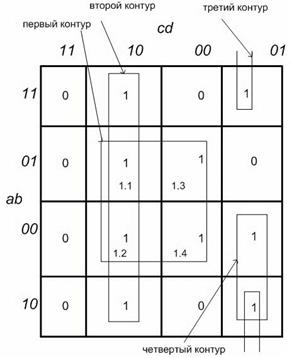
Соответствующая ему схема приведена на рисунке 3.15.
Рисунок 3.15 – Логическая схема для минимизированного Логического выражения 4. Основные термины и определения цифровой схемной логики.
ДНФ – дизъюнктивно-нормальная форма – представление логического выражения в виде суммы произведений. Инверсия – операция НЕ – логическое действие, при котором появление хотя бы одного логического нуля на входе даёт логический нуль на выходе. Инвертор – логический элемент, реализующий операцию НЕ. КНФ – конъюктивно-нормальная форма – представление логического выражения в виде произведения сумм. Логическая переменная – переменная, значение которой может быть равно либо логическому нулю, либо логической единице. Логическая схема – схема, состоящая из логических элементов. Логическая функция – функция, включающая в себя логические переменные, значение которой может быть равно либо логическому нулю, либо логической единице. Логический элемент – графическое представление элементарной логической функции. Логическое отрицание – операция НЕ, инверсия – логическое действие, при котором происходит изменение состояния на противоположное. Логическое сложение – операция ИЛИ, дизъюнкция – логическое действие, при котором появление хотя бы одной логической единицы на входе даёт логическую единицу на выходе. Логическое умножение – операция И, конъюнкция – логическое действие, при котором появление хотя бы одного логического нуля на входе даёт логический нуль на выходе. Таблица истинности – таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции. ДНФ– дизъюнктивно-нормальная форма – представление логического выражения в виде произведения сумм. КНФ– конъюнктивно-нормальная форма – представление логического выражения в виде суммы произведений. Минтерм– это полное произведение всех входных переменных, соответствующее одной строке таблицы истинности, в которой значение выходной переменной (значение функции) равно логической 1. Переменная входит в минтерм с инверсией, если её значение в строке истинности равно 0. Каноническая сумма минтермов – это логическая сумма всех минтермов, которая представляет собой максимальное логическое выражение, соответствующее таблице истинности. Карта Карно– графическое представление таблицы истинности. Макстерм– это сумма всех входных переменных, соответствующее одной строке таблицы истинности, в которой значение выходной переменной (значение функции) равно 0. Переменная входит в макстерм с инверсией, если её значение в строке истинности равно 1. Каноническое произведение макстермов– это логическая сумма всех макстермов, которая представляет собой максимальное логическое выражение, соответствующее таблице истинности.
Краткие итоги
Любая цифровая вычислительная машина состоит из логических схем. Логические схемы, в свою очередь, состоят из логических элементов. Самыми простыми логическими элементами являются элементы И, ИЛИ и НЕ. Им соответствуют функции логического умножения, сложения и инверсии. Работа логической схемы наиболее наглядно может быть описана с помощью таблицы истинности. Возможно и решение обратной задачи – по известной таблице истинности синтезировать логическое выражение и логическую схему. Для синтеза схем применяется метод минимизации с помощью карт Карно. Наиболее рациональная логическая схема может быть синтезирована по минимизированному логическому выражению.
Набор для практики Вопросы для самопроверки 1. Нарисуйте элементы И на два, четыре и пять входов, составьте для каждого из них таблицу истинности, напишите соответствующее каждому элементу логическое выражение. 2. Нарисуйте элементы ИЛИ на три, четыре и пять входов, составьте для каждого из них таблицу истинности, напишите соответствующее каждому элементу логическое выражение. 3. Нарисуйте элементы И-НЕ на два, четыре и пять входов, составьте для каждого из них таблицу истинности, напишите соответствующее каждому элементу логическое выражение. 4. Нарисуйте элементы ИЛИ-НЕ на три, четыре и пять входов, составьте для каждого из них таблицу истинности, напишите соответствующее каждому элементу логическое выражение. 5. Какой уровень сигнала является решающим для логического сложения? для логического умножения? для функции И-НЕ? для функции ИЛИ-НЕ?
Для логического сложения решающим является уровень логической 1. Уровень логического 0 является решающим для логического умножения. Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1. Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0.
6. Что такое таблица истинности?
Таблица истинности – это таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции. 7. Сколько строк в таблице истинности для 5-входовой логической схемы? для 4-входовой? для 2-входовой? 32, 16, 4
8. Функция скольких переменных описывается таблицей истинности длиной 4 строки? 64 строки? 512 строк? 2, 6, 9
Основные логические функции и элементы, их таблицы истинности, схемы и условно-графические обозначения.
|
||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 884; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

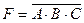 , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
, но при этом из контекста должно быть ясно, что данное умножение именно логическое;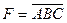 ;
;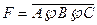 ;
; .
.
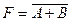 , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
, но при этом из контекста должно быть ясно, что данное сложение именно логическое;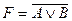 .
.
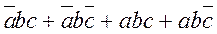 , в которой не изменяется только переменная «b ». Второй контур охватывает две единицы. Ему соответствует сумма минтермов
, в которой не изменяется только переменная «b ». Второй контур охватывает две единицы. Ему соответствует сумма минтермов 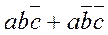 , в которой переменная «b » принимает оба возможных значения, а произведение
, в которой переменная «b » принимает оба возможных значения, а произведение 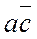 остается неизменным. Таким образом, получаем минимальное выражение:
остается неизменным. Таким образом, получаем минимальное выражение: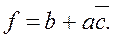 (3.3)
(3.3)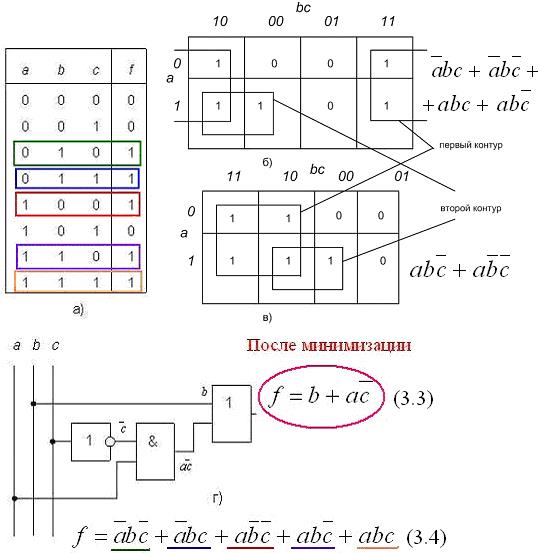
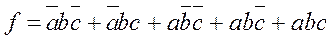 (3.4)
(3.4)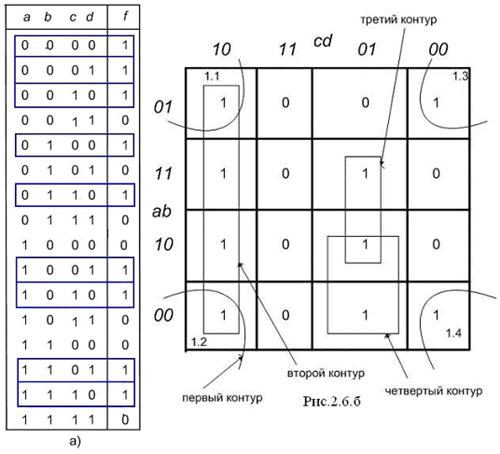
 , равными 01 и 00 и между сочетаниями
, равными 01 и 00 и между сочетаниями 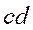 , равными 10 и 00. А на рисунке 3.14 представлена развертка этого же торроида, "разрезанная" между комбинациями
, равными 10 и 00. А на рисунке 3.14 представлена развертка этого же торроида, "разрезанная" между комбинациями