Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейный дискриминантный анализ
Пусть теперь в k -мерном признаковом пространстве имеются два облака точек { Xi }и { Yj }, i = 1,…, n, j = 1,…, m. Они характеризуются своими центрами a 1 и a 2 и своими ковариационными матрицами S1, S2, вместо которых рассматривают соответствующие выборочные матрицы рассеяния S 1 = (n - k) Рассмотрим формальную постановку этой задачи. Пусть имеются две квадратичные формы С T AC и С T B С с симметричными положительно-определенными матрицами A и B. Требуется найти единичный вектор С, являющийся решением следующей оптимизационной задачи:
Предположим, что для второй формы уже найдено удовлетворительное значение: С T B С = b, b > 0. Будем решать задачу
а условие нормировки
и приравняем нулю ее производные по С и по λ:
Отсюда сразу следует, что при любом b искомый вектор С* должен быть собственным вектором пучка квадратичных форм { A, B }, соответствующим одному из его собственных чисел λ*, при этом вспомним также об условии
Таким образом, решение задачи состоит в том, что С – единичный собственный вектор пучка { A, B }, соответствующий его минимальному собственному числу λ. Это диктует два подхода к решению исходной задачи об оптимальном проектировании. 1. В качестве матрицы А выбираем сумму ковариационных матриц рассматриваемых совокупностей: A = Σ1+Σ2. Это означает, что минимизируется сумма внутренних дисперсий проекций CT Σ1 C + CT Σ2 C. В качестве матрицы В выбираем произведение расстояний между центрами исходных облаков: B = (a 1- a 2)(a 1- a 2) T, тогда CTBC =[(CTa 1 C - CTa 2 C) (CTa 1 C - CTa 2 C) T ]= (CTa 1 C - CTa 2 C)2 – квадрат расстояния между центрами облаков-проекций. Недостаток этого подхода в том, что матрица В имеет ранг 1, поэтому у пучка { A, B } имеется единственное собственное подходящее собственное число λ. Данный подход обеспечивает проектирование только на прямую, что дает единственную дискриминантную компоненту.
2. В качестве матрицы А снова выбираем сумму ковариационных матриц Σ1+Σ2, а в качестве В – ковариационную матрицу объединенного облака. При этом минимизируется сумма внутривыборочных дисперсий проекций и одновременно максимизируется их межвыборочная дисперсия. Это позволяет получить любое число Элементы вектора С можно интерпретировать как веса, отражающие важность каждой компоненты векторов X, Y при разделении исходных совокупностей. Если используется несколько дискриминантных компонент, это соответствует различным независимым точкам зрения на X, Y. Иногда дискриминантным компонентам удается приписать некий физический смысл – тогда можно говорить о дискриминантных факторах. Пример 5.4. Для двух данных k -мерных выборок X = [ X 1, X 2,…, Xn ], Y = [ Y 1, Y 2,…, Yn ] (
Пример 5.5. Смоделировать две независимые 3-мерные выборки с заданными параметрами и представить их
Рис.5.2. Результат работы программы (Документ 5.4) Задание на лабораторную работу
· В виде 3-мерных облаков точек; · На плоскости 2 главных факторов; · На плоскости 2 главных дискриминантных факторов. Контрольные вопросы
|
||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.87.156 (0.008 с.) |
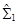 и S 2 = (m - k)
и S 2 = (m - k)  .Обычно бывает выгодно с самого начала перейти к безразмерным величинам, поделив каждую компоненту на соответствующее ей СКО. Поставим задачу о выборе направления проектирования следующим образом: будем требовать, чтобы рассеяние внутри облаков – проекций было минимальным и при этом эти облака разошлись как можно дальше друг от друга.
.Обычно бывает выгодно с самого начала перейти к безразмерным величинам, поделив каждую компоненту на соответствующее ей СКО. Поставим задачу о выборе направления проектирования следующим образом: будем требовать, чтобы рассеяние внутри облаков – проекций было минимальным и при этом эти облака разошлись как можно дальше друг от друга.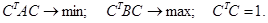

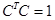 учтем позднее. Составим функцию Лагранжа
учтем позднее. Составим функцию Лагранжа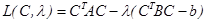

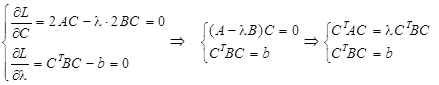 .
.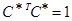 . Вычислим соответствующее значение функции Лагранжа или, что то же самое, значение минимизируемой функции:
. Вычислим соответствующее значение функции Лагранжа или, что то же самое, значение минимизируемой функции:
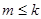 дискриминантных компонент, соответствующих m минимальным собственным числам пучка { A, B }.
дискриминантных компонент, соответствующих m минимальным собственным числам пучка { A, B }.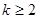 ) найти коэффициенты двух главных дискриминантных факторов по матрицам рассеяния и определить долю информации, объясняемую этими факторами.
) найти коэффициенты двух главных дискриминантных факторов по матрицам рассеяния и определить долю информации, объясняемую этими факторами.