Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация на основе линейных дискриминантных форм
Разделяющие поверхности, построенные на основе сравнения дискриминантных информантов, могут иметь достаточно сложный вид, поэтому иногда бывает более удобно отказаться от оптимальных методов и использовать в качестве разделяющей поверхности гиперплоскость, определяя ее параметры из условия минимума ошибок распознавания. Вместо самих измерений рассмотрим их проекции на вектор C. Этот вектор определяется либо на основе метода главных компонент, либо на основе одной из идей линейного дискриминантного анализа. Вектор C является нормалью к гиперплоскости, разделяющей рассматриваемые облака точек. Закон распределения проекции z = CTX зависит от класса W i, к которому принадлежит Х. Решающее правило имеет вид:
В случае двух гауссовых классов с параметрами (a 1, Σ1) и (a 2, Σ2) для измерения Х из i -го класса его проекция
поэтому ошибки классификации вычисляются следующим образом:
Оптимальное значение свободного члена v находят из условия P (e) = p 1 P 1 + p 2 P 2 = min. В принципе, можно сразу минимизировать P (e) по двум переменным, C и v. Пример 7. 4. Построение разделяющей прямой в двумерном пространстве. В условиях примера 13.1 p 1 = p 2 = 0.5; X = (x, y) T, Выберем направление проектирования, при котором достигает максимума расстояние между проекциями центров классов: C =(Σ1+Σ2) -1(a 1- a 2). Находим:
Согласно формулам (13.9),
учитывая, что p 1 = p 2 = 0.5, находим вероятность ошибочной классификации:
Дифференцируя по v и приравнивая производную нулю, получаем для нахождения v уравнение
P 1=1 – Φ(2.86) = 0.002; P 2 = Φ(-2.86) = 0.002. Пример 7.5. Сценарий в ИМС MatLab.
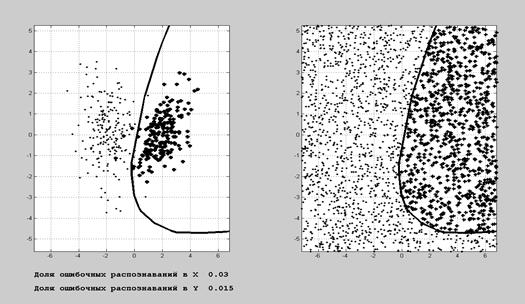
Рис. 7.4. Результат работы программы из Документа 7.1 Пример 7.6. Сценарий в ИМС MatLab.
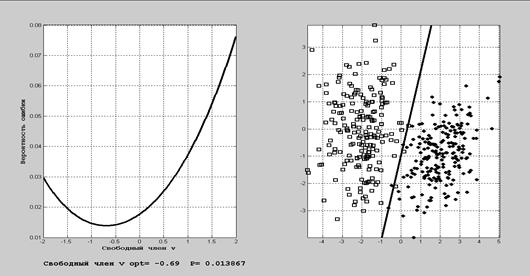
Рис.7.5. Результат работы программы из Документа 7.2 Задания на лабораторную работу 1. Смоделировать две 3-мерные выборки (n =100) из нормального закона с различными средними и ковариационными матрицами. 2. Произвести классификацию полученных данных 3 различными способами.
3. Проанализировать зависимость результатов классификации от расстояния Махаланобиса между исходными классами. 4. Перейти к плоскости главных компонент и изобразить на ней зоны притяжения каждого из классов. Контрольные вопросы Знать основные определения теории классификации в линейном и нелинейном вариантах, технологии построения дискриминантных информантов в одномерном и многомерном случаях. КЛАСТЕРНЫЙ АНАЛИЗ Кластерный анализ (автоматическая классификация, распознавание образов без учителя, таксономия, кластер-анализ) – это совокупность методов, подходов и процедур, предназначенных для разбиения исследуемой совокупности на подмножества относительно сходных между собой объектов (кластеры, таксоны, классы). В основе лежит неформальное предположение о том, что объекты, относимые к одному кластеру, должны иметь большее сходство между собой, чем с объектами других кластеров.
|
||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 73; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.121.214 (0.007 с.) |
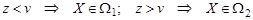 .
.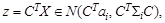
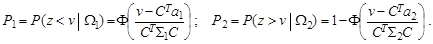 (7.9)
(7.9)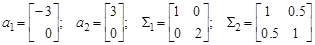 .
.
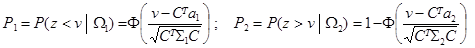 ,
,
 откуда v = -0.13,
откуда v = -0.13,