Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Главные компоненты и факторный анализ
Пусть случайный вектор X = (x 1, …, xk ) T Î Nk (a, å). Первой главной компонентой вектора X называется линейная комбинация
где коэффициенты с 1 i выбираются так, чтобы величина z 1 имела наибольшую дисперсию среди всех нормированных линейных комбинаций компонент xi. Дисперсия случайной величины
поэтому вектор C 1 является решением оптимизационной задачи
затем приравняем нулю ее производные по векторному аргументу C и скалярному аргументу λ:
Первое уравнение приводится к виду Подставим найденные варианты значений вектора C в исходную целевую функцию:
Таким образом, максимальное значение дисперсии z, равное λmax(Σ), достигается, если вектор C – нормированный собственный вектор ковариационной матрицы Σ, соответствующий ее максимальному собственному числу λmax(Σ). Геометрически это означает, что вектор С 1 параллелен наибольшей оси эллипсоида рассеяния вектора Х. Поскольку суммарная дисперсия всех компонент вектора X
говорят, что доля суммарной дисперсии, объясняемая первой главной компонентой z 1, равна
Аналогично, с использованием второго по величине собственного числа l2 и соответствующего собственного вектора С 2, ортогонального, как известно, С 1, определяется вторая главная компонента и т.д. Векторы С 1, С 2 и т.д. можно получать также непосредственно из решения оптимизационных задач:
и т.д. Геометрически переход от вектора Х к его первым двум главным компонентам означает его проектирование на плоскость, параллельную главным осям эллипсоида рассеяния. На практике матрица å обычно неизвестна, и ее заменяют матрицей Пример 5.1. Определение линейной главной компоненты для двумерного вектора. Пусть X = (x, y) T Î N 2(0, å); Прежде всего, находятся собственные числа матрицы å:
Далее определяется собственный вектор С = (с 1, с 2) Т, соответствующий наибольшему собственному числу l1 = 2.21, из системы уравнений
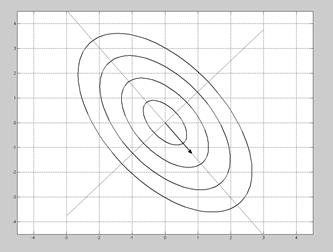
Этот вектор C задает направление главной оси х 1. Ось у 1 ей перпендикулярна; ее направление можно также определить как собственный вектор, соответствующий второму собственному числу λ2. Ортогональность этих осей обеспечивается симметрией матрицы Σ. На рис. 5.1 приведен эллипс рассеяния для вектора Х. Направление его главной оси задается найденным вектором С. В осях х 1, у 1 этот эллипс описывается уравнением
Доля дисперсии, объясняемой первой главной компонентой, l1/(l1 + l2) = 74%. Таким образом, размерность вектора уменьшается в два раза, а эффективность представления - только на 26%.
Рис. 5.1. Семейство эллипсов рассеяния в примере 4.1 Данную технику, как правило, применяют при анализе k -мерной совокупности однотипных измерений – k -мерного облака точек X 1,…, Xn, которые трактуют как независимые измерения случайного вектора X. Для параметров a, å используют их выборочные оценки. Если компоненты вектора Х имеют различную физическую природу и измерены с помощью качественно различных технических средств, то результат не имеет, как правило, ясного физического смысла и существенно зависит от выбора масштаба. В этих случаях вместо ковариационной матрицы å или ее оценки используют корреляционную матрицу с элементами ri j = s i j (s i i s jj )-1/2, которые являются безразмерными величинами (диагональные элементы rii = 1). Главные компоненты, построенные по корреляционной матрице – безразмерные случайные величины – называют главными факторами, объясняющими рассеяние компонент вектора X. Традиционный факторный анализ использует несколько иную технику вычислений коэффициентов cij – факторных нагрузок, основанную на методе наименьших квадратов. Его результаты обычно очень близки к результатам анализа главных компонент по корреляционной матрице, однако в факторный анализ органически входит специальный метод вращений, призванный облегчить содержательную интерпретацию получающихся факторов. Пример 5.2. Для данной k -мерной выборки X = [ X 1, X 2,…, Xn ] (
Есть два пути для выявления физического смысла найденных факторов. Во-первых, можно проанализировать веса cij. Во-вторых, можно просто расположить исходные объекты, описываемые измерениями X, в порядке возрастания i -го фактора и попытаться понять, какому физическому свойству соответствует такое упорядочение. Линейные главные компоненты обладают целым рядом других оптимальных свойств, которые в некоторых случаях можно использовать даже в качестве их начального определения. Пусть X 1, …, Xn, Xi = (x i 1, …, xik) T - независимая выборка из распределения Nk (a, å), a z 1, …, zn - их образы при линейном проектировании в некоторое q – мерное пространство (q < k):
Пусть d i j - расстояние между Xi и Xj в евклидовом пространстве Rk, r ij - расстояние между их образами в Rq. В качестве меры искажения матрицы попарных расстояний используется величина
Имеет место следующее важное свойство: D q 2 минимально, если в качестве Zi взяты первые q главных компонент векторов X 1, …, Xn. На этом свойстве, в частности, основаны различные нелинейные аналоги метода главных компонент, которые получаются, если рассматривать меры искажения, отличные от (4.1). Пример 5.3. Несколько лет назад в одном из российских НИИ решалась следующая задача. Имелось около 300 образцов смазочных материалов, отечественных и импортных. Каждый образец анализировался по 9 параметрам. Таким образом, исходная информация представляла собой облако точек в 9-мерном пространстве. При проектировании этого облака на плоскость двух первых главных факторов величина
оказалась равной 0.64, т.е. потери информации при проектировании составили около 36%. Анализ выявленных факторов позволил выделить 14 сгустков (кластеров), в каждый из которых вошли материалы с достаточно близкими свойствами, что дало основания для рекомендаций по замене импортных материалов их отечественными аналогами. 32 точки при этом оказались изолированными - это материалы, не имеющие аналогов и не допускающие замены.
|
||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.102.112 (0.01 с.) |
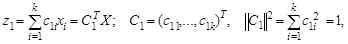
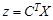
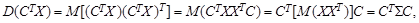
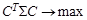 с ограничением
с ограничением 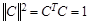 . Составим для этой задачи функцию Лагранжа
. Составим для этой задачи функцию Лагранжа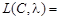
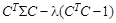 ,
,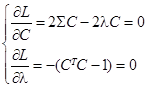 .
.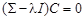 : точками, подозрительными на экстремум, являются пары собственных чисел и соответствующих собственных векторов матрицы Σ. Второе уравнение показывает, что собственные векторы должны иметь единичную длину.
: точками, подозрительными на экстремум, являются пары собственных чисел и соответствующих собственных векторов матрицы Σ. Второе уравнение показывает, что собственные векторы должны иметь единичную длину.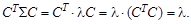
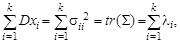
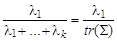 .
.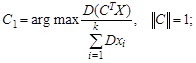
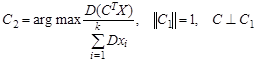
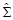 , полученной на основе обучающей выборки Х 1, …, Хn.
, полученной на основе обучающей выборки Х 1, …, Хn.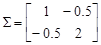 .
.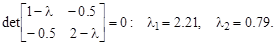
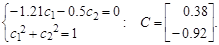
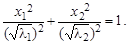
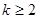 ) найти коэффициенты двух главных факторов и определить долю информации, объясняемую этими факторами.
) найти коэффициенты двух главных факторов и определить долю информации, объясняемую этими факторами.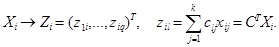
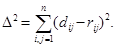 (4.1)
(4.1)