
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многомерный нормальный законСодержание книги
Поиск на нашем сайте Пусть a = (a 1, a 2,…, ak) T – известный k -мерный вектор, Σ = [σ i j ] – известная матрица размерности k × k, обладающая следующими свойствами:
Известно, что любая матрица, обладающая такими свойствами, может выступать в качестве ковариационной матрицы некоторого невырожденного k -мерного случайного вектора. В частности, если для двух величин (k =2) заданы их дисперсии σ12, σ22 и коэффициент корреляции ρ, -1≤ρ≤1, то их ковариационную матрицу всегда можно записать в виде
При k >2 набор коэффициентов корреляции может оказаться противоречивым, поэтому матрицу, построенную по аналогии с (3.1), нужно отдельно проверять на положительную определенность. Пусть теперь k -мерный случайный вектор X = [ ξ1,…, ξ k ] T подчиняется непрерывному закону распределения с плотностью f (x), где x = [ x 1,…, xk ] T, вида
В этом случае говорят, что вектор X подчиняется k -мерному нормальному закону с параметрами a, Σ: Приведем без доказательства основные свойства k -мерного нормального закона. Доказательства, сводящиеся к вычислению соответствующих многомерных интегралов, можно найти в любом достаточно подробном курсе теории вероятностей.
Легко видеть, что соответствующая поверхность уровня имеет вид
где
и представляет собой в силу условия Σ>0 эллипсоид в k -мерном пространстве Rk с центром в точке a и направлениями осей, задаваемыми собственными векторами матрицы Σ (или Σ-1). Семейство таких соосных эллипсоидов Q (с), получающихся из (3.3) при различных значениях с, называется семейством эллипсоидов рассеяния вектора X (рис.3.1 b):
Рис.3.1. Типичный вид плотности 2-мерного нормального закона и ее линий уровня 5. Для случайных векторов имеют место предельные теоремы, аналогичные тем, которые рассматриваются в одномерном случае. Теорема. Пусть X 1 ,…, Xn,… - последовательность независимых одинаково распределенных k -мерных случайных векторов, M Xi = a, cov Xi = B. Тогда
(сходимость по вероятности). Квадратичная форма, стоящая в левой части (3.2), может рассматриваться как квадрат расстояния между векторами X и a. Его называют расстоянием Махаланобиса:
Имеет место следующий факт: rM 2(X, a) подчиняется хи-квадрат распределению с k степенями свободы. Таким образом,
где
Вообще, нахождение для нормального вектора
осуществляется легко только в трех случаях:
Более сложные интегралы чаще всего приходится вычислять по методу Монте-Карло (см. ниже пример 3.3). Пример 3.1. Решение. Умножение на матрицу – линейная операция, все компоненты вектора Y являются линейными функциями от компонент X, поэтому Y – m -мерный гауссов вектор. Остается найти его математическое ожидание и ковариационную матрицу. Имеем: M Y = M(GX) = G M X = Ga; Cov(Y) = M(Y 0 Y 0 T) = M[ GX 0(GX 0) T ] = M[ G (X 0 X 0 T) GT ] = G M(X 0 X 0 T) GT = G Σ GT, Y 0 = Y – M Y, X 0 = X – X 0. Пример 3.2. X = [ x 1, x 2] T – гауссов случайный вектор, средние его компонент равны нулю, дисперсии σ12=1, σ22=4, коэффициент корреляции ρ = -0.5. Какой угол образует его главная ось с осью Ox? Решение. Ковариационная матрица вектора X
Найдем ее собственные числа и собственные векторы оператором [ C, L ] = eig(Σ). Главной оси отвечает минимальное собственное число матрицы
|
||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.006 с.) |

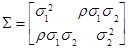 (3.1)
(3.1)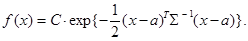 (3.2)
(3.2)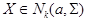 или что X является гауссовым случайным вектором. Легко проверить, что при k =1, когда матрица содержит единственный элемент σ11= σ2>0, формула (3.2) сводится к известной формуле для плотности одномерного нормального закона с нормирующей константой
или что X является гауссовым случайным вектором. Легко проверить, что при k =1, когда матрица содержит единственный элемент σ11= σ2>0, формула (3.2) сводится к известной формуле для плотности одномерного нормального закона с нормирующей константой 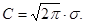 Типичный вид поверхности z = f (x) при k =2 и ее линий уровня приведен на рис.3.1 a, b.
Типичный вид поверхности z = f (x) при k =2 и ее линий уровня приведен на рис.3.1 a, b.
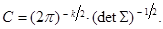

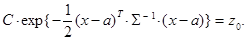
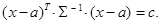 (3.3)
(3.3)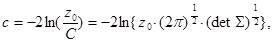 (3.4)
(3.4)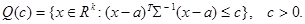 (3.5)
(3.5)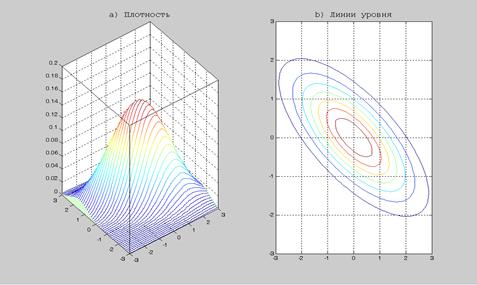

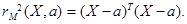
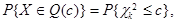 (3.6)
(3.6)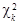 - случайная величина, распределенная по закону χ2(k). В частности, при k = 2 формула (3.6) имеет особенно простой вид:
- случайная величина, распределенная по закону χ2(k). В частности, при k = 2 формула (3.6) имеет особенно простой вид: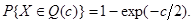 (3.7)
(3.7)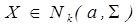 вероятности попадания в область
вероятности попадания в область 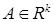 , сводящееся к вычислению многомерных интегралов
, сводящееся к вычислению многомерных интегралов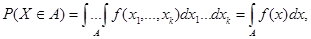
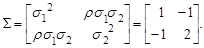
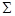 (оно же – максимальное собственное число матрицы
(оно же – максимальное собственное число матрицы 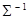 ) и первый столбец матрицы C, его компоненты – это косинус и синус искомого угла φ. Отсюда находим, что cos(φ)=0.8507, sin(φ)=0.5257, так что φ=0.5535 (рад) = 31.7154о.
) и первый столбец матрицы C, его компоненты – это косинус и синус искомого угла φ. Отсюда находим, что cos(φ)=0.8507, sin(φ)=0.5257, так что φ=0.5535 (рад) = 31.7154о.


