Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерии значимости. Задача о выборе из двух гипотез
Задачи как теоретической, так и прикладной статистики часто формулируют как некие азартные игры человека с Природой, при этом в прикладной статистике от Природы ожидают особенной изощренности и коварства. Пусть имеется случайная выборка x 1,…, xn с теоретическим распределением F (x,θ), где θ – неизвестный параметр. Для теоретических рассуждений это означает, что x 1,…, xn – независимые одинаково распределенные (н.о.р.) случайные величины с общим распределением F (x,θ). Любая функция от них T (x 1,…, xn) – статистика – сама является случайной величиной с каким-то распределением G (x,θ). На практике x 1,…, xn – это числа, случайные реализации величин xi, T (x 1,…, xn) – число, случайная реализация величины Т. Рассмотрим задачу проверки статистической гипотезы H 0: θ = θ0 против альтернативной гипотезы H 1: θ = θ1. В такой постановке ее называют задачей о выборе из двух гипотез. В игровой форме это значит, что Природа выбрасывает нам случайные числа x 1,…, xn, подчиняющиеся распределению F (x,θ), а мы должны угадать, какое значение θ она использовала, θ0 или θ1. Результатом выступает решающее правило (критерий): n -мерное пространство разбивается на две непересекающиеся области, Ω0 и Ω1; если точка Любое решающее правило предполагает два типа ошибок.
Вероятность ошибки 1-го рода обозначают α; величина 1-α называется уровнем значимости. Вероятность ошибки 2-го рода обозначают β; величина 1-β называется мощностью критерия. Критерий, обладающий наибольшей мощностью для всех альтернатив и при любых α, называется равномерно наиболее мощным. Такие критерии встречаются редко и, в основном, наперечет известны. Для подавляющего большинства гипотез существует множество конкурирующих критериев, каждый из которых является наиболее мощным для какого-то класса альтернатив. Замечание. Ошибки α и β неравноправны. Например, в военных приложениях обычно Н 0 – это гипотеза о наличии цели. Тогда α – это вероятность пропуска цели, β – вероятность ложной тревоги.
Обычно решающее правило стараются сформировать на основе какой-то статистики T (Х) = T (x 1,…, xn) – статистики критерия. При этом уже не n -мерное пространство, а вещественная прямая разбивается на непересекающиеся зоны В 0 и В 1: если
Важную подсказку при выборе статистики критерия Т дает лемма Неймана-Пирсона. Она утверждает, что Т должна быть монотонной функцией от отношения функции правдоподобия выборки x 1,…, xn при θ = θ0 и такой же функции правдоподобия при θ = θ1. Распределение статистики Т в условиях, когда верна Н 0, называется ее центральным распределением. Ее распределение в условиях, когда верна Н 1, называется нецентральным. Статистику Т всегда стараются сформировать так, чтобы ее центральное распределение хотя бы асимптотически совпадало с каким-то стандартным распределением, для которого есть таблицы или программы вычисления его функции распределения. В жизни часто бывает невозможно явно сформулировать альтернативную гипотезу, так что Н 0 проверяется против произвольной альтернативы. В этом случае контролируется только уровень значимости 1-α, и предполагается, что сама конструкция решающего правила обеспечивает его достаточную мощность 1-β при всех возможных альтернативах. Такие критерии называются критериями значимости. При этом важно не завысить уровень значимости: при уменьшении α неизбежно возрастает ошибка β (и наоборот). Пример 6.1. По стандарту при выпечке на 1000 сладких булочек должно приходиться 10000 изюмин. Из большой партии случайным образом выбрано 10 булочек. Число изюмин xi в них оказалось следующим:
Нулевая гипотеза состоит в том, что стандарт соблюдается и пекарь не ворует изюм. Как ее проверить? Построим математическую модель процесса попадания изюмин в булочки. Пусть V – объем теста, из которого получается 1000 булочек, v – объем, из которого должна получиться данная конкретная булочка. В объем V бросается N =10000 изюмин, для каждой из которых имеется вероятность p = v / V =0.001 попадания в выбранную булочку. Таким образом, речь идет о схеме случайного блуждания (схеме Бернулли) с числом испытаний N и вероятностью успеха p. N достаточно велико, p достаточно мала, предположение о независимости испытаний возражений не вызывает. Число успехов x, т.е. число изюмин, попавших в данную булочку, должно в этих условиях аппроксимироваться законом Пуассона π(λ) с параметром λ = = N p = 10.
Для независимых случайных величин
Это означает, что для нашей выборки
Таким образом, если стандарт соблюдается, то случайная величина
должна подчиняться стандартному нормальному закону N (0,1). Для рассматриваемой выборки
Это означает, что если бы мы много раз повторяли эксперимент, выбирая каждый раз по 10 булочек, то, при условии полного соблюдения стандарта, такой результат мог бы встретиться примерно в 9% случаев. Вывод: либо нам крупно не повезло, либо стандарт все-таки нарушается и пропадает примерно 13% изюма. Гипотеза о недостаче принимается на уровне 1- 0.09 = 0.91. Вообще говоря, этот уровень недостаточно высок, так что рекомендация состоит в том, что пекарь находится под сильным подозрением и наблюдения (контрольные закупки) следует продолжить.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.44.23 (0.01 с.) |
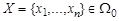 , то принимается гипотеза H 0, в противном случае – альтернатива H 1. Область Ω1 называют при этом критической областью.
, то принимается гипотеза H 0, в противном случае – альтернатива H 1. Область Ω1 называют при этом критической областью.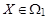 , поэтому ошибочно принята альтернатива H 1;
, поэтому ошибочно принята альтернатива H 1; 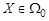 , поэтому ошибочно принята гипотеза H 0.
, поэтому ошибочно принята гипотеза H 0.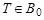 , принимается гипотеза H 0, если
, принимается гипотеза H 0, если 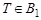 , принимается альтернативная гипотеза H 1. Таким образом,
, принимается альтернативная гипотеза H 1. Таким образом,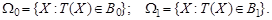 .
.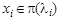 выполняется соотношение (теорема Райкова)
выполняется соотношение (теорема Райкова)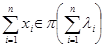 .
.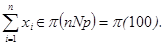 Но при больших λ для закона Пуассона действует аппроксимация нормальным законом: если
Но при больших λ для закона Пуассона действует аппроксимация нормальным законом: если 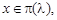 то при
то при 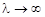
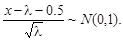
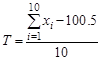
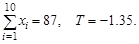 По таблицам функции распределения нормального закона Ф(х) находим, что
По таблицам функции распределения нормального закона Ф(х) находим, что