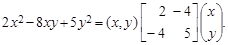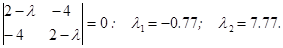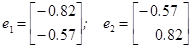Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискриминантные информанты и классификация
Пусть в k -мерном вещественном пространстве Rk действуют независимо друг от друга два случайных механизма. Первый выдает случайные векторы X, подчиняющиеся закону распределения с плотностью f 1(x), второй - f 2(x). Класс векторов Х, выданных первым механизмом, обозначим W1, вторым - W2. Пусть также известны априорные вероятности срабатывания каждого из этих механизмов p 1 и p 2, p 1+ p 2=1. Для данного вектора X требуется принять решение, к какому классу он принадлежит, W1 или W2. Решающее правило состоит в разбиении пространства Rk на две области W 1 и W 2 так, что если X Î Wi, то принимается решение X ÎW i. Рассмотрим сначала одномерный случай, k =1 (рис.7.1). Решающее правило имеет вид: Если
Вычислим производную по T * от обеих частей последнего выражения и приравняем ее нулю: - p 1 f 1(T *) + p 2 f 2(T *) = 0. Рис.7.1. Одномерный случай Это значит, что правило, минимизирующее вероятность ошибочного распознавания, должно быть основано на выражении di = pi fi (x):
В случае произвольной размерности k выражение d i (X) = pi fi (X) (7.1) называют дискриминантным информантом вектора Х для класса W i. При этом байесово классификационное правило имеет вид: Х принадлежит тому из классов W i, для которого его дискриминантный информант максимален. Величина ri представляет ожидаемую долю ошибочных распознаваний для объектов класса W i , а r - для объектов всех классов. Данное правило минимизирует математическое ожидание числа ошибочных распознаваний. Можно строить решающие правила на основе других принципов, например, минимизируя максимальную компоненту вектора средних потерь { r i }. Каждое из таких правил совпадает с некоторым байесовым правилом при соответствующем выборе pi. Приведенную конструкцию можно усложнять, рассматривая величины lij, i, j = 1, 2 - потери от отнесения вектора X ÎW i к классу W j. Выражение (7.1) для дискриминантного информанта можно упрощать, подвергая монотонным преобразованиям и отбрасывая члены, не зависящие от i. Если классы задаются k -мерными нормальными распределениями Nk (ai ,å i),то, логарифмируя равенство (10.1) и отбрасывая члены, не зависящие от i, получим
Граница областей W 1 и W 2 оказывается при этом поверхностью второго порядка в Rk. Пример 7.1. Построение разделяющей кривой в двумерном пространстве. Пусть p 1 = p 2 = 0.5; X = (x, y) T, Прежде всего, необходимо вычислить значения дискриминантных информантов (общее слагаемое ln(0.5) отбрасываем):
Уравнение разделяющей кривой d 1(X) = d 2(X) приводится к виду ln(2) + (x+ 3)2 + 0.5 y 2 = ln(0.75) + 4 / 3(x- 3)2 – 4/3(x- 3) y + 4/3 y 2 или, в эквивалентной форме, 2 x 2 - 8 xy + 5 y 2 – 84 x + 24 y = -12.12. (7.3) Уравнение (13.3) описывает кривую второго порядка на плоскости. Выделяя в нем полные квадраты, приводим его к виду
Для приведения этого уравнения к каноническому виду рассмотрим квадратичную форму
Ее собственные числа l1, l2 определяются из уравнения
Нормированные собственные векторы этой квадратичной формы
определяют базис, в котором её матрица имеет диагональный вид. Соответствующее преобразование переменных определяется формулами x = -0.82 x 1–0.57 y 1; y = -0.57 x 1+0.82 y 1. Отсюда получаем уравнение разделяющей кривой в новых переменных x 1, y 1 в каноническом виде:
В данном случае разделяющая кривая представляет собой гиперболу, график которой приведен на рис. 13.2 а),б).При попадании точки Х в выделенную заливкой область W 2 принимается гипотеза Х ÎW2. Левая половина области W 2 на рис.13.2 а), очевидно, относится к чрезвычайно мало вероятным значениям X и физического смысла не имеет, но при некритическом подходе может оказаться источником грубых ошибок. Если å1 = å2 = å, то разделяющая поверхность представляет собой гиперплоскость, в двумерном случае - прямую. Если при этом р 1 = р 2, то решающее правило удобно интерпретировать с помощью расстояния Махаланобиса D (X, ai ). Правило распознавания в этом случае называют методом ближайшего соседа: Х относится к тому из классов W i, центр которого аi оказывается ближе.
Приведенные рассуждения легко обобщить на случай произвольного числа классов.
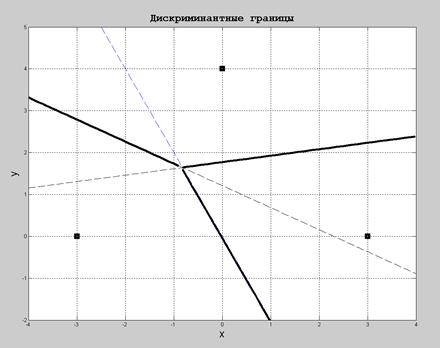
Рис. 7.2. Разделяющая кривая в примере 7.1 Пример 7.2. Построение разделяющих прямых в двумерном пространстве для трех классов. Пусть p 1 = p 2 = p 3 = 1/3; X = (x, y) T , å1 = å2 = å3 =å;
В этом случае квадраты расстояний Махаланобиса выражаются формулами: DM 2(X, a 1) = 4/7[(x+ 3)2 + (x+ 3) y + 2 y 2]; DM 2 (X, a2) = 4/7[(x- 3)2 + (x- 3) y + 2 y 2]; DM 2 (X, a 3) = 4/7 [ x2 + x (y- 4)+ 2(y- 4)2]. Приравнивая эти выражения попарно, получаем три разделяющие прямые: DM 2 (X, a 1) = DM 2(X, a 2): 2 x + y = 0; DM 2 (X, a 1) = DM 2(X, a 3): 10 x + 19 y – 23 = 0; DM 2 (X, a 2) = DM 2 (X, a 3): 2 x - 13 y + 23 = 0. Соответствующие зоны W 1, W 2, W 3 показаны на рис. 7.3. В общем k - мерном случае если ковариационные матрицы классов совпадают, то при отбрасывании в (13.2) членов, не зависящих от i, выражение для дискриминантного информанта получается в виде линейной функции от Х: di (X) = ln pi + a iT å -1 X – 0.5 a iT å-1 ai. (7. 4)
Рис. 7.3. Разделяющие прямые в примере 7.2 Вообще, для любых плотностей вида f (x) = C j [(x - b) T S (x - b)], x Î Rk, где С - нормирующая константа; b - постоянный вектор; S - симметричная матрица, границы зон состоят из кусков плоскостей и поверхностей второго порядка в R. Если плотности f 1(x) и f 2(x) не заданы, их приходится оценивать по обучающим выборкам, описывающим классы Ω1 и Ω2. В гауссовом случае достаточно получить выборочные оценки средних и ковариационных матриц этих обучающих выборок. В других случаях используют непараметрические сглаженные оценки плотностей f 1(x) и f 2(x), которые строятся по этим обучающим выборкам, причем результаты могут значительно отличаться в зависимости от использованной процедуры сглаживания.
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 129; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.202.72 (0.018 с.) |
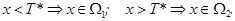 Границей между ними является значение x = T *.
Границей между ними является значение x = T *.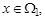 то вероятность ошибки r 1 = 1- F 1(T *); если
то вероятность ошибки r 1 = 1- F 1(T *); если 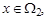 то вероятность ошибки r 2 = F 2(T *). Учитывая априорные вероятности p 1 и p 2, получаем, что границу T * нужно определять из условия минимума байесовского риска
то вероятность ошибки r 2 = F 2(T *). Учитывая априорные вероятности p 1 и p 2, получаем, что границу T * нужно определять из условия минимума байесовского риска
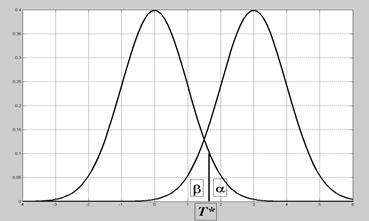
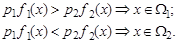
 (7.2)
(7.2)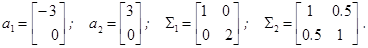
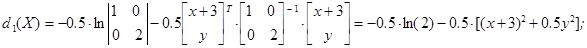
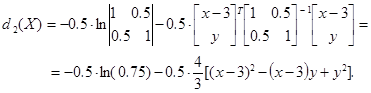
 (7.4)
(7.4)