
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы дифференциальных уравнений и матричная экспонента
Решение дифференциального уравнения для функций одной переменной
Решение системы дифференциальных уравнений
exp(At) – матричная экспонента, представляющая собой матрицу той же размерности, что и А. Т.обр., все трудности, связанные с решением системы, скрыты в конструкции матричной экспоненты. Если матрица несимметрична, то часть компонент Y может оказаться мнимой. Рассматриваемая схема сохраняется, если Y сама является матрицей той же размерности, что и A. В частности, в теории массового обслуживания приходится решать систему уравнений Чепмена-Колмогорова
Решение с учетом начальных условий имеет вид Π(t)=exp(Λ t). Как отмечалось выше, если у квадратной матрицы X все собственные числа λ1,…,λ n различны или если X симметрична, она допускает представление X = C -1 LC, где L – диагональная матрица, на диагонали которой стоят собственные числа матрицы X, L =diag(λ1,…,λ n), С – матрица, столбцами которой являются нормированные собственные векторы X. В этом случае exp(X) = C -1 exp(L) C, exp(L) = diag[ exp(λ1),…,exp(λ n) ]. Если среди собственных чисел есть совпадающие, то для вычисления матричной экспоненты простыми методами можно использовать отрезок соответствующего степенного ряда:
Существуют крайне эффективные алгоритмы, позволяющие быстро вычислять любую функцию от матрицы. В частности, в ИМС MatLab для матричной экспоненты имеются операторы expm(X), expm1(X), expm2(X), expm3(X), основанные на различных математических подходах. При некоторых дополнительных предположениях рассмотренную схему можно использовать для приближенного решения еще более сложных нелинейных систем вида
модифицированный метод Эйлера – к соотношениям
и т.д., где выражения в квадратных скобках представляют собой первые слагаемые разложения
Эта форма широко используется, в частности, при решении систем стохастических дифференциальных уравнений. Пример 2.5. Решить систему дифференциальных уравнений Явное решение. Запишем систему в матричных обозначениях: Матрица A имеет собственные числа
Отсюда получаем общее решение x = C 1 x 1+ C 2 x 2, y = C 1 y 1+ C 2 y 2. Группируя однородные члены и вводя новые произвольные константы, получаем общее решение в виде
Из начальных условий находим С 1=1, С 2=2. Численное решение. Пример 2.6. Найти производную обратной матрицы Решение.
Это прекрасно согласуется с известной формулой для функций одной переменной Пример 2.7. Решение. Матрица X симметрична, поэтому ее можно привести к диагональному виду, при этом ее собственные числа вещественны, а собственные векторы ортогональны. Применяя в ИМС Matlab оператор [ C, L ]=eig(X), находим
|
|||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 1395; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.154.208 (0.005 с.) |
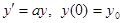 осуществляется чрезвычайно просто:
осуществляется чрезвычайно просто: (2.5)
(2.5)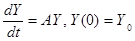 , где Y – вектор-столбец размерности < n ×1>, A – матрица < n × n > так, как оно излагается в обычных курсах математического анализа, неизмеримо сложнее. Однако на языке функций матричного аргумента решение полностью аналогично (2.5):
, где Y – вектор-столбец размерности < n ×1>, A – матрица < n × n > так, как оно излагается в обычных курсах математического анализа, неизмеримо сложнее. Однако на языке функций матричного аргумента решение полностью аналогично (2.5):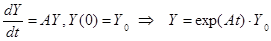 ,
, или
или 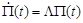 с начальным условием
с начальным условием  где
где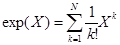 .
.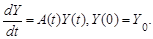 Для моментов времени
Для моментов времени 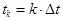 метод Эйлера приводит к рекурсии
метод Эйлера приводит к рекурсии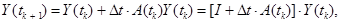
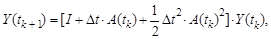
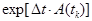 в степенной ряд. Говорят, что эти соотношения описывают приближенное решение нелинейной системы в аддитивной форме. Матричная экспонента приводит к аналогичной рекурсии в более точной мультипликативной форме:
в степенной ряд. Говорят, что эти соотношения описывают приближенное решение нелинейной системы в аддитивной форме. Матричная экспонента приводит к аналогичной рекурсии в более точной мультипликативной форме:
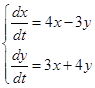 c начальными условиями x (0) = 1, y (0) = -2.
c начальными условиями x (0) = 1, y (0) = -2.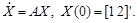
 , им соответствуют собственные векторы (1; i) и (1; - i). Они определяют 4 фундаментальных решения:
, им соответствуют собственные векторы (1; i) и (1; - i). Они определяют 4 фундаментальных решения: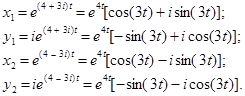
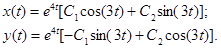
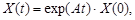 нужно только располагать удобным алгоритмом вычисления матричной экспоненты.
нужно только располагать удобным алгоритмом вычисления матричной экспоненты.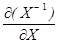 .
. Правая часть этого тождества – величина постоянная, ее производная по X равна нулю. Вычислим производную от обеих частей тождества:
Правая часть этого тождества – величина постоянная, ее производная по X равна нулю. Вычислим производную от обеих частей тождества: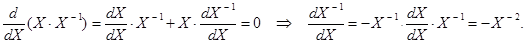
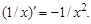
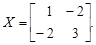 Найти sin(X) и exp(X).
Найти sin(X) и exp(X).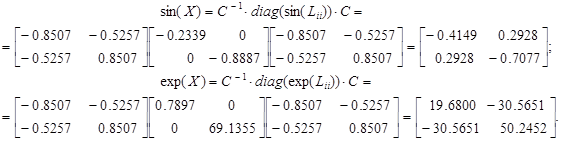 .
.


