
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы нелинейных уравнений и матрица Якоби
Пусть дана дифференцируемая функция одной вещественной переменной y = f (x). Требуется найти корни уравнения f (x) = 0. Пусть x ( k ) и x ( k +1) – два последовательных приближения для одного из корней. Представим функцию в виде отрезка ряда Тейлора
Пренебрежем остатком R и будем считать второе приближение настолько точным, что f (x ( k +1)) пренебрежимо мало по сравнению с остальными слагаемыми. Тогда из (2.1) получается ряд последовательных приближений
Доказывается, что при достаточно слабых ограничениях эта последовательность сходится к одному из корней уравнения f (x) = 0, к какому – определяется выбором начального приближения x (0). У каждого корня существует своя область притяжения: если x (0) выбрано в зоне притяжения корня x *, то последовательность (2) сойдется к x *. Замечание. Вместо точной формулы для производной можно использовать ее приближенное значение Применим эти соображения для решения системы n нелинейных уравнений c n неизвестными F (X)= 0 или, в развернутом виде,
Если все функции fi (X) дифференцируемы, то F (X) называют дифференцируемым отображением
В векторно-матричных обозначениях аналогом (2.1) выступает формула F (X (k +1) ) = F (X (k) ) + J (X (k) ) [ X (k +1) – X (k) ] + R, где J – матрица частных производных или матрица Якоби отображения F: J (X) = Аналог (2.2) – метод последовательных приближений для решения системы уравнений F (X)= 0 – получается на основе тех же соображений, что и в одномерном случае и имеет вид X (k +1) = X (k) – J -1(X (k)) F (X (k) ). (2.3) Каждое решение системы имеет свою область притяжения: если начальное приближение X (0) лежит в области притяжения решения X *, то последовательность (2.3) сойдется к X *. Процесс (2.3) предполагает многократное вычисление обратной матрицы J -1. Может случиться, что на каком-то шаге определитель J окажется равным нулю. В таких случаях предусматривают обходной путь: если J -1 не существует, то в (3) используют матрицу (J +ε E)-1, где E – единичная матрица < n × n >, а ε – малое число, которое может уменьшаться с ростом номера итерации k.
Пример 2.1. Решить уравнение e 0.1 x - x 2=0 (см. рис. 2.1).
Решение. Коварство этого уравнения в том, что у него не 2 корня, как может показаться из рис.2.1, а три. Это следует из того, что экспонента всегда растет быстрее степенной функции, поэтому при очень больших x обязательно должно появиться еще одно пересечение графиков. Уравнение решается по формуле (2.2). Если начальное приближение x (0)<0.04, приходим к корню x *=-0.9534. Если начальное приближение x (0) от 0.06 до примерно 71, приходим к корню x *=1.0541. Если начальное приближение x (0)>78, приходим к корню x *=89.9951.
Рис.2.1. Итерационное решение нелинейного уравнения из Примера 2.1 Во всех этих случаях требуется всего 3-4 итерации. Если x (0) находится в одной из промежуточных зон, процесс все равно приходит к одному из трех корней, но для этого может потребоваться порядка 20 итераций. Неустойчивость может возникнуть, если на одной из итераций производная окажется слишком близкой к нулю. Пример 2.2. Решить систему уравнений Решение. Итерационный процесс имеет вид
При начальном приближении x (1)=1, y (1)=1 значение корня x *=0.7391, y *=0.6736 достигается уже на третьей итерации. Второй корень x *=-0.7391, y *=-0.6736 находится либо сразу из соображений симметрии, либо при отрицательных значениях начального приближения. Зоны притяжения корней примерно разделяются биссектрисой 1-го и 3-го координатных углов, при этом вблизи границы зон возникает неопределенность за счет возможных малых значений определителя матрицы Якоби.
|
|||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.135.224 (0.006 с.) |
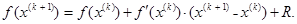 (2.1)
(2.1)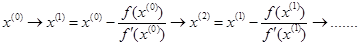 (2.2)
(2.2)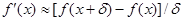 с малым приращением δ.
с малым приращением δ.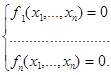
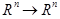 . В этом случае каждую из функций fi можно представить в виде, аналогичном (6.1):
. В этом случае каждую из функций fi можно представить в виде, аналогичном (6.1):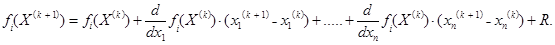
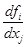 (X).
(X).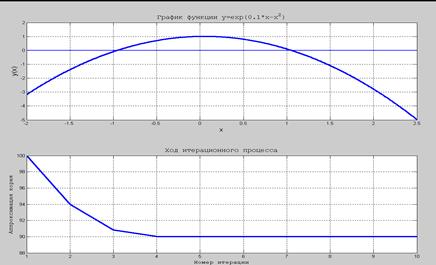
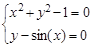 .
.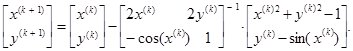 (2.4)
(2.4)


