
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Степень чувствительности и значимости переменнойСодержание книги
Поиск на нашем сайте
Величины по проекту: принятие решения
Чем ближе переменная к верхнему левому углу, тем важнее прогнозировать ее с максимальной точностью. Переменные величины, расположенные в нижнем правом углу, возможно, приблизятся к ожидаемым значениям и не будут пересматриваться. Они вряд ли повлияют на конечные результаты даже при ошибочном прогнозе. Очевидно, что для оценок, приведенных в табл. 8.4, потребуется мнение менеджмента. Вводимые переменные, указанные в графе с пометкой «проверить позже», должны быть внимательно изучены как наиболее важные для расчета чистой текущей стоимости NPV. Возможно, не стоит скупиться на оценку этих переменных с максимальной точностью. Переменные величины, указанные в графе с пометкой «внимательно проследить», также должны быть тщательно оценены с тем, чтобы гарантировать их разумную величину.
Анализ чувствительности ставки дисконта И продажной цены
Рассмотрим несколько иной подход, включающий анализ чувствительности ставки дисконта и продажной цены [16]. Фирма анализирует проект инвестиций. Проводимый анализ чувствительности состоит из следующих шагов: 1. Установление зависимости между основными переменными величинами (количеством продаж, продажной ценой единицы, жизнью проекта и т.п.) и чистой текущей стоимостью NPV. 2. Определение диапазона изменений и наиболее приемлемого значения каждой из основных переменных. 3. Изучение эффекта изменения чистой текущей стоимости в зависимости от изменения основных переменных (как правило, однократного изменения одной переменной). Зависимость для чистой текущей стоимости имеет вид
где NPV– чистая текущая стоимость проекта; Q – количество ежегодных продаж, единиц; Р – продажная цена единицы; V – переменные издержки на единицу; F – общие постоянные издержки без амортизации и расходов по проценту; D – величина ежегодной амортизации; Т – ставка налога на прибыль; R – ставка дисконта, в качестве которой используется средневзвешенная стоимость капитала; n – число лет экономической жизни проекта; I – начальные инвестиции; S – чистая остаточная стоимость.
В табл. 8.5 представлен диапазон наиболее приемлемых оценок основных переменных.
Таблица 8.5 Диапазон оценок Основных переменных Переменные |
Диапазон |
Наиболее желаемая оценка | |||||||||||||||||||||||
| 1 | 2 | 3 | ||||||||||||||||||||||||
| Q | 1000 – 2000 | 1600 | ||||||||||||||||||||||||
| P | 600 – 1000 | 750 | ||||||||||||||||||||||||
| V | 300 – 500 | 400 | ||||||||||||||||||||||||
| Окончание таблицы 8.5 | ||||||||||||||||||||||||||
| 1 | 2 | 3 | ||||||||||||||||||||||||
| F | 120000 – 120000 | 120000 | ||||||||||||||||||||||||
| D | 160000 – 160000 | 160000 | ||||||||||||||||||||||||
| T | 0,6 – 0,6 | 0,6 | ||||||||||||||||||||||||
| R | 0,08 – 0,11 | 0,1 | ||||||||||||||||||||||||
| n | 5-5 | 5 | ||||||||||||||||||||||||
| S | 400000 – 400000 | 400000 | ||||||||||||||||||||||||
| I | 1200000 – 1200000 | 1200000 | ||||||||||||||||||||||||
Получая диапазон приемлемых оценок основных переменных, мы можем изучить влияние каждой переменной на чистую текущую стоимость.
Иллюстрацией подобного анализа служат зависимости между:
1) ставкой дисконта R и чистой текущей стоимостью NPV;
2) продажной ценой Р и чистой текущей стоимостью NPV.
Зависимость между R и NPV для наиболее желаемых оценок наших переменных:
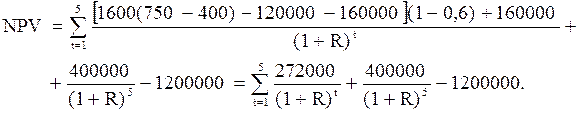
| R | 8% | 9% | 10% | 11% |
| NPV | 158080 | 118080 | 79552 | 42700 |
Зависимость между P и NPV:
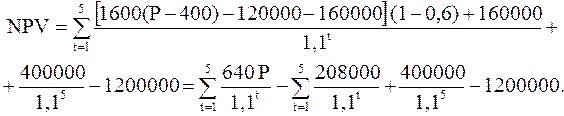
| P | 600 | 700 | 750 | 800 | 900 | 1000 |
| NPV | -284384 | -41760 | 79552 | 200864 | 443488 | 686112 |
Графически это выглядит следующим образом.
 |
Рис. 8.1
Используя полученные результаты анализа чувствительности, мы показываем, как чистая текущая стоимость меняется при разных неблагоприятных изменениях основных переменных:
| Неблагоприятное процентное изменение | Оценка R | Чистая текущая стоимость NPV |
| 5 10 15 20 | 10,5 11,0 11,5 12,0 | 60418 42700 24681 7575 |
| Неблагоприятное процентное изменение | Оценка R | Чистая текущая стоимость NPV |
| 5 10 15 20 | 713 675 638 600 | 10308 102500 192267 284384 |
Графически совмещённый анализ выглядит следующим образом
 |
Рис. 8.2
Анализ чувствительности довольно популярен как метод оценки риска. Он заслуживает внимания, т. к. нацеливает менеджмент на выявление недостатков переменных величин и их составляющих; показывает, насколько прочно или уязвимо неблагоприятное изменение вводимых переменных проекта; выявляет необходимость анализа более отдаленной будущей деятельности. Если NPV и IRR имеют высокую чувствительность к некоторым переменным, то это следует учесть в будущей информации об этих переменных. Эффективное управление должно предусматривать сценарии непредвиденных обстоятельств.
АНАЛИЗ ВАРИАНТОВ РАЗВИТИЯ СОБЫТИЙ
Анализ чувствительности, концентрируя внимание на самых важных вводимых переменных, имеет существенный недостаток. Экономические связи, существующие между переменными, часто разрушают предпосылки этого анализа: высокая величина одной переменной ведет к низкой величине какой-либо другой переменной и наоборот. Для малых проектов, в которые не надо вводить данные из верхнего левого угла таблицы чувствительности переменных, это, возможно, не проблема. Даже если принято «плохое» решение, оно не сильно отразится на бизнесе фирмы. Однако для проектов с большим объемом инвестиций и величинами, присутствующими в верхнем левом углу табл. 8.4, нужны дальнейшие исследования с более реалистичными предпосылками о взаимосвязи переменных. Подобный анализ носит название вариантного, или анализа вариантов развития событий.
Исходный пример, рассмотренный в анализе чувствительности проекта инвестиций в оборудование, будет использован в качестве ожидаемого варианта развития событий. Кроме него будут разработаны еще два варианта развития событий: оптимистический и пессимистический. Первый дает разумные обнадеживающие оценки проекта на случай более благоприятного развития событий вопреки ожиданиям, а второй - если все плохое, что может случиться, произойдет на самом деле. Пример вариантного анализа приведен в табл. 9.1. Оба варианта должны быть внутренне последовательными. Целью анализа является изучение области наибольших отклонений распределения продаж или чистой текущей стоимости.
Эти распределения настолько точны, насколько вводимые данные отражают оценку экстремальных условий. Менеджмент обычно успешно справляется с оценкой таких результатов.
За исключением очень крупных проектов, в которых задействованы значительные инвестиции, вариантный анализ позволяет менеджменту получить достаточное представление о характеристиках рентабельности проекта.
Таблица 9.1
Вариантный анализ инвестиционного проекта
| Пессимистический: | Количество единиц проданной продукции сократилось на 10 % Продажная цена сократилась на 15 % Переменные издержки возросли на 10 % Ликвидационная стоимость сократилась на 25 % Оборотный капитал – требуется дополнительно 10 % Покрыта только 1/2 оборотного капитала Ставка дисконта – 15 % Чистая текущая стоимость = –1253,89 Внутренняя ставка рентабельности =7,56% |
| Ожидаемый: | Чистая текущая стоимость = +3945,77 Внутренняя ставка рентабельности = = 27, 79% |
| Оптимистический: | Количество единиц проданной продукции увеличилось на 5% Продажная цена не изменилась Переменные издержки сократились на 10% Ликвидационная стоимость увеличилась на 5% Оборотный капитал – требуется сокращение на 10% Покрыт весь оборотный капитал Ставка дисконта = 9% Чистая текущая стоимость = +4265,44 Внутренняя ставка рентабельности = 28,91% |
Если распределение вероятностей и взаимосвязь между переменными могут быть оценены и введены в компьютер, появляется возможность разработать тысячи статистически последовательных вариантов. В этом случае можно подойти к анализу степени риска, называемому моделированием Монте-Карло.
|
| Поделиться: |

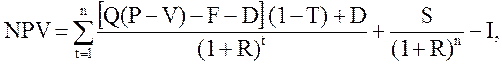 (8.1)
(8.1)


