
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика корректировки ставки дисконтаСодержание книги
Поиск на нашем сайте
Очевидно, что вложения капитала, связанные с большим или меньшим риском, могут быть оправданны лишь в тех случаях, когда расчетная норма рентабельности на вложенный капитал будет превышать аналогичный показатель при условии вложения капитала в безрисковые проекты. Безрисковый коэффициент дисконтирования в основном соответствует государственным ценным бумагам. Более рисковыми являются облигации, акции, и еще более – вложения капитала в реальные активы. Чем больше риск, связанный с проектом, тем выше должна быть «премия» за риск. Учесть это можно добавлением «премии» к безрисковому коэффициенту дисконтирования. Общая методика корректировки ставки дисконта будет выглядеть следующим образом: - устанавливается исходная «цена» капитала Rо; - определяется экспертным путем риск, связанный с каждым проектом; - величина риска для каждого проекта соотносится с размером «премии» (величиной прироста ставки дисконта). В качестве первого приближения прирост ставки дисконта при определении экономической эффективности инвестиций в энергетические объекты с новыми техническими решениями рекомендуется принимать в размере dR = =0,03...0,1; - для каждого проекта рассчитывается NPV с коэффициентом дисконтирования R = Rо + dR; - проект с большим значением NPV считается предпочтительнее. ВРЕМЕННОЙ АСПЕКТ ИЗМЕНЕНИЯ СТОИМОСТИ ДЕНЕГ Одна денежная единица сегодня не равна денежной единице завтра, так как деньги обесцениваются во времени. В основе принятия решений, учитывающих изменение стоимости денег, лежат два основных постулата финансов: 1. Никогда не рискуйте, если вы не получите адекватной компенсации за этот риск. 2. Нельзя сравнивать две суммы денег, которые относятся к разным периодам времени, игнорируя временной аспект стоимости денег. Изменение стоимости денег во времени учитывается с помощью ставок дисконта, в качестве которых используются ставки рентабельности или нормы прибыли. Выбор правильной ставки дисконта стоит в одном ряду с такими важнейшими проблемами анализа планируемых инвестиций, как объективная характеристика проекта и разумная оценка движения потоков денежных средств. Процесс формирования ставки дисконта включает такие понятия, как реальная норма прибыли, номинальная норма прибыли с учетом инфляции, с учетом риска. Реальная норма прибыли зависит от желаемой задачи на инвестируемый капитал, не учитывающей инфляцию и риск. Рассмотрим две альтернативы: Сегодня 1. Потратить 1000000 и получить удовольствие сегодня. 2. Дать в долг 1000000, отказавшись от сегодняшнего потребления и связанных с ним удовольствий. Через год 1. Ничего не останется на потребление. 2. Получить долг с процентами и наслаждаться потреблением в более поздний период.
Таким образом, если нас просят отказаться от чего-то ценного, то нам должны предоставить компенсацию за этот отказ. Компенсация, необходимая инвесторам или кредиторам в целях стимулирования отказа от потребления денег в настоящее время, называется чистой временной (текущей) стоимостью денег, или чистой ставкой процента. Предположим, что по окончании года на сумму 1000000 было выплачено 1030000. Норма прибыли по состоявшейся сделке:
Величина RR, составившая в нашем примере 3%, также называется реальной нормой прибыли, или реальной ставкой рентабельности без учета риска. Временной аспект стоимости денег построен на решении проблем предпочтений. Что предпочтительнее: 1000000 сегодня или 1030000 через год? Рассмотрим три варианта кредита:
Допустим, что предприятие предпочитает иметь 1000000 сегодня, нежели 1029999 через год, либо 1030001 через год, нежели 1000000 сегодня. Следовательно, для фирмы нет разницы между 1000000 сегодня и 1030000 через год. Ввиду отсутствия различия между двумя денежными суммами в разные периоды времени можно утверждать, что 1000000 сегодня является финансовым эквивалентом 1030000 через год. Финансовый эквивалент позволяет заменить одну сумму другой, изменяя при этом распределение движения денежных средств по срокам и не оказывая влияния на структуру предпочтений по данному вопросу. Норма прибыли, лежащая в основе составления финансовых эквивалентов, будет называться реальной, необходимой нормой прибыли без учета риска. В этом случае работает следующее правило: отказаться от потребления в настоящее время (предоставить кредит, инвестировать), если норма прибыли, которую вы ожидаете получить, превышает ту, что вам необходима, и отказаться от предоставления кредита или инвестиций, если ожидаемая норма прибыли ниже необходимой. Решим проблему предпочтений для необходимой реальной нормы прибыли 3%: получить сегодня А = 2345967 или через год Б = 2415928?
В = А (1 + RR), или В = 2345967 ∙ 1,03 = 2416346,01.
Величина А = 2345967 сегодня и величина В = 2416346,01 через год являются финансовыми эквивалентами. В этом случае А = В, В > Б, следовательно, А > Б. Поэтому А предпочтительнее сегодня, чем Б через год. Вычисления можно провести по-другому:
С позиции финансового эквивалента нет разницы между 2345561,17 сегодня и 2415928 через год. А и Г принадлежат к одному и тому же периоду времени, поэтому Б = Г, А > Г, следовательно, А > Б. Рассмотренные примеры отражают фундаментальный процесс решения сложных задач по инвестициям: – использование необходимой нормы прибыли (требуемой ставки рентабельности) для выявления отношений безразличия во времени путем расчета финансовых эквивалентов; – определение предпочтений между начальным движением денежных средств и финансовых эквивалентов; – использование приоритетов, относящихся к данной проблеме.
Корректировка на инфляцию В стабильных экономических условиях темпы инфляции невысоки и прогнозируются достаточно точно. Предположим, что в следующем году ожидается темп инфляции 3,5%. Для того, чтобы сделать поправку на инфляцию, нам необходимо: 1) учесть RR = 3% в качестве компенсации за отложенное потребление:
1000000 (1 + 0,03) = 1030000;
2) в целях сохранения покупательной способности денег стоимость каждой денежной единицы необходимо увеличить на 3,5%:
1030000 (1 + 0,035) = 1066050.
Объединим оба вычисления в одном выражении:
1000000(1 + RR)(1 + Н) = 1000000 ∙ 1,03 ∙ 1,035 = 1066050.
Осуществляя поправку на инфляцию, мы использовали формулу Ирвинга Фишера. Эта формула раскрывает особенности учета инфляционного фактора:
(1 + RR) (1 + Н) = 1 + RR + Н + RR ∙ H, (5.2)
где Н – темп инфляции.
Принимая инвестируемую сумму за единицу, мы получаем спустя некоторое время (1 + RR) благодаря приращению капитала по реальной ставке RR. Однако из-за темпа инфляции Н денежный поток необходимо увеличить в (1 + Н) раз. Прибавляя RR и Н, мы вносим корректировку в начальную сумму 1000000. Кроме этого, требуется корректировка на темп инфляции 3,5% суммы наращения 30000, полученной в качестве компенсации за отложенное потребление по реальной ставке. Следует заметить, что при работе с малыми ставками RR и Н западные экономисты обычно игнорируют произведение RR и Н из-за его ничтожной величины. Во всех остальных случаях можно допустить большие погрешности. Впрочем, прогнозирование темпов при высокой инфляции само по себе создает возможности больших неточностей. Таким образом, учитывая ставку RR = 3% в качестве компенсации за отложенное потребление и прогнозируемый темп инфляции Н = 3,5%, мы получаем номинальную норму прибыли (номинальную ставку рентабельности) без учета риска:
Rн = 1, 03 ∙ 1,035 – 1 = 1,06605 – 1 = 0,06605 или 6,605%.
6,605% – 3% = 3,605% – инфляционная премия. 3,605% – 3,5% = 0,105% – добавочная премия для корректировки RR на снижение покупательной способности денежной единицы. Предположим, что требуемая предприятием процентная ставка по кредиту, или ставка дисконта по инвестициям, установлена на уровне 14%. Появление разности (14% – 6,605% = =7,395%) будет обусловлено риском.
Корректировка на риск Рассмотрим два альтернативных проекта инвестиций, в один из которых требуется вложить 1000 денежных единиц.
Очевидно, что большинство инвесторов по причине наименьшего риска предпочтет проект А.
Предположим, что имеется еще проект В:
Сравнивая А и В по степени риска получения отдачи на инвестиции, мы видим, что проект В более рисковый. Однако этот проект обещает и большую норму прибыли. Многие инвесторы, возможно, предпочтут проект В, так как ради более высокого результата стоит пойти на повышенный риск. Возвращаясь к номинальной норме прибыли с учетом риска в 14%, мы говорим, что фирма добавляет премию за риск в размере 7,395% к номинальной норме прибыли без учета риска Rн = 6,605%. В этом случае с точки зрения инвестора 1000000 сегодня является финансовым эквивалентом 1140000, которые он рассчитывает получить через год. Номинальная ставка с учетом риска будет вычисляться по следующей формуле:
R = (1 + Rн) (1 + R') – 1
или R = 1,06605 – 1,069368 – 1 = 0,14 или 14%,
где ставка риска R' рассчитывается или задается предприятием.
Западные фирмы довольно часто работают с инфляционными премиями и премиями за риск. Однако в условиях высокой инфляции ставки за риск, наряду с прогнозом темпа роста инфляции, могут иметь большие погрешности. Нормы прибыли (ставки рентабельности) участвуют в качестве ставок дисконтирования денежных потоков и вычисляются по формулам сложных процентов.
ПРОЕКТИРОВАНИЕ ДВИЖЕНИЯ ДЕНЕЖНЫХ СРЕДСТВ Рассмотрим процесс оценки нового инвестиционного проекта на примере расширения бизнеса. Маркетинговые исследования позволяют предположить, что достигнутый в настоящее время уровень продаж фильтров для воды в 1000 единиц может быть повышен в ближайшие 5 лет до 2000 единиц в год. Чтобы обеспечить ожидаемый спрос на следующие пять лет, необходимо приобрести оборудование стоимостью 6000. Ликвидационная стоимость к концу пятого года должна составить 1000. Новое оборудование разместится на пустующей площади, поэтому инвестиции в производственные площади не понадобятся. Расширение производства потребует дополнительного чистого оборотного капитала, который, по оценкам бухгалтера, составит 800. Однако вся сумма в полном объеме потребуется только к пятому году. Ежегодное увеличение чистого оборотного капитала ожидается в размере 160. Оценивая движение денежных средств, предположим, что отток капитала происходит в начале года, а приток – в конце. Установка нового оборудования на действующем предприятии изменит активы: СЕЙЧАС: количество продаж – 1000 ед. Денежные средства 500 Кредиторы 600 Дебиторы 500 Запасы 1000 2000 Чистый оборотный капитал = 2000 – 600 = 1400.
ЧЕРЕЗ 5 ЛЕТ: количество продаж – 2000 ед. Денежные средства 500 Кредиторы 1000 Дебиторы 900 Запасы 1800 3200 Чистый оборотный капитал = 3200 – 1000 = 2200. Прирост чистого оборотного капитала = 2200 – 1400 = 800.
Проектируя оттоки в начале, а притоки - в конце года, мы стремимся к получению более реалистичной модели движения денежных средств. Кроме движения капитала, мы должны рассмотреть движение денежных средств от основной (операционной) деятельности. Поскольку прогноз с инфляцией на ближайшие пять лет затруднителен, то воспользуемся реальным анализом. Оценим проект в единицах одинаковой покупательной способности. Расчет представлен в табл. 6.1-6.3.
Таблица 6.1
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.74.192 (0.012 с.) |
||||||||||||||||||||||||||||||||

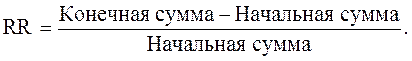 (5.1)
(5.1)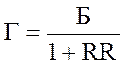 , или Г = 2415928/1,03 = 2345561,17.
, или Г = 2415928/1,03 = 2345561,17.


