
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения в различных моделях
Математический анализ как анализ переменных величин с момента своего появления развивался в тесной связи с естествознанием, и в частности с физикой и механикой. Потребности развития физических наук, необходимость количественного изучения движения и меняющихся процессов привели к возникновению и формированию основных понятий дифференциального исчисления и интегрального исчисления. В очень большом числе случаев физические законы описывают некоторые соотношения между величинами, характеризующими изучаемый процесс, и скоростью изменения этих величин. Другими словами, эти законы выражаются равенствами, в которых участвуют неизвестные функции и их производные. Такие равенства называются дифференциальными уравнениями. Они появляются как математическая форма записи ряда физических законов. Изучение процессов, описываемых этими законами, сводится к изучению свойств решений дифференциальных уравнений. Размножение бактерий. На опытах с бактериями установлено, что скорость размножения бактерий пропорциональна их количеству, если, конечно, для них имеется достаточный запас пищи. Так как сами бактерии очень малы, а их количество велико, то можно считать, что масса бактерий с течением времени меняется непрерывно. Тогда скорость прироста массы бактерий называется скоростью размножения. Если через число x(t) обозначить массу всех бактерий в момент времени t, то По условию x(t) и x/(t) неотрицательные, поэтому коэффициент k тоже неотрицательный. Уравнение (1) является простейшим примером дифференциального уравнения. Оно называется дифференциальным уравнением размножения. Искомым неизвестным уравнения Решением данного уравнения является функция вида x = Cekt, где С – const. Действительно,
Радиоактивный распад. Опытом установлено, что скорость распада радия в каждый момент времени пропорциональна начальному количеству радия. Таким образом, если через x(t) обозначить массу вещества, еще не распавшегося к моменту времени t, то скорость распада
Уравнение Биология. Модель Лотки — Вольтерры – первая содержательная математическая модель, описывающая биологическое сообщество (если не считать исследований Фибоначчи популяции кроликов, приведших его к знаменитым числам, носящим его имя, а также исследований Мальтуса, приведших впоследствии к известному уравнению x ′ = ax (a > 0) мальтузианского роста). Она описывает популяцию, состоящую из двух взаимодействующих видов. Первый из них, именуемый хищниками, при отсутствии второго вымирает по закону
а второй — жертвы — при отсутствии хищников неограниченно размножается в соответствии с законом Мальтуса. Взаимодействие двух этих видов моделируется так. Жертвы вымирают со скоростью, равной числу встреч хищников и жертв, которое в данной модели предполагается пропорциональным численности обеих популяций, т. е. равной dxy (d > 0). Поэтому
Хищники же размножаются со скоростью, пропорциональной числу съеденных жертв:
(c > 0). Система уравнений
На рисунке видно, что численности популяций хищников и жертв совершают рассогласованные по фазе автоколебания. Медицина. Применение дифференциальных уравнений в медицине продемонстрируем на примере простейшей математической модели эпидемии. В модели описывается распространение инфекционного заболевания в изолированной популяции. Особи популяции делятся на три класса. Инфицированный класс численностью x (t) (t — время) состоит из инфицированных (заболевших) особей, каждая из этих особей заразна (предполагается, что инкубационный период заболевания пренебрежимо короток). Второй класс численностью y (t) составляют восприимчивые особи, т. е. особи, которые могут заразиться при контакте с инфицированными особями. И, наконец, третий класс состоит из невосприимчивых особей (приобретших иммунитет или погибших в результате заболевания). Его численность обозначается z (t). Предполагается также, что общая численность популяции n постоянна (т. е. не учитываются рождения, естественные смерти и миграция). Две гипотезы, лежащие в основе модели таковы:
1) заболеваемость в момент времени t равна x (t) y (t) (эта гипотеза основывается на правдоподобном предположении, что число заболевающих пропорционально числу встреч между больными и восприимчивыми особями, которое в свою очередь в первом приближении пропорционально x (t) y (t)); таким образом численность класса x растет, а численность класса y убывает со скоростью ax (t) y (t) (a > 0); 2) численность становящихся невосприимчивыми особей (приобретших иммунитет или погибших) растет со скоростью, пропорциональной численности заболевших, т. е. со скоростью bx (t) (b > 0). В результате мы получаем систему уравнения
Физические основы реографии Реография – это метод оценки состояния (параметров) кровеносного русла путем измерения полного сопротивления (импеданса) участка ткани или органа переменному току. Формула полного сопротивления биотканей переменному току:
Для уменьшения емкостного сопротивления используют высокую частоту. Измерения проводятся на частоте 30 кГц. При увеличении частоты увеличивается выделение тепла, что приводит к изменению состояния кровеносного русла. При частоте 30 кГц влиянием емкостных сопротивлений тканей и крови пренебрегают, поэтому Выведем зависимость изменения объема крови в сосуде в соответствии с изменением полного сопротивления участка кровеносного русла:
Чтобы найти изменения объема
Знак “–” в формуле указывает на то, что если сопротивление кровотока уменьшается, то объем крови увеличивается, и наоборот. Реограмма – это график зависимости пульсових изменений импеданса от времени (см. рис.).
bcd – инцезура; bcde – катакрота;
А – амплитуда анакроты; В – амплитуда инцезуры; С – амплитуда катакроты; Т – длительность одного сердечного цикла. Задача 1. Найти закон движения тела по оси Ox, если оно начало двигаться из точки М(4;0) со скоростью v = 2 t + 3 t2. При прямолинейном движении скорость есть производная от пути по времени. Обозначим путь через x, имеем v = Решим уравнение:
Используя начальные условия, найдем C. Так как x = 4 при t = 0, то подставив эти значения в общее решение, находим: С = 4. Таким образом, закон движения тела выражается формулой Задача 2. Найти кривые, для которых угловой коэффициент касательной в каждой точке на любой из этих кривых равен абсциссе точки касания. По геометрическому смыслу производной
Задача 3. Определить путь, который пройдет автомобиль за время t=20 с, если его скорость пропорциональна пути и если за 10с. автомобиль проходит 100м, а за 15с- 200м. По условию Отсюда: При t=10, s=100: ln100=10k+C При t= 15, s=200:ln200= 15k+C, следовательно k=ln2/5, тогда С=ln25 Уравнение При t=20c. S=400м. Задача 4. При брожении скорость прироста действующего фермента пропорциональна его первоначальному содержанию. Определить содержание фермента через 4ч после брожения, если вместо 2г первоначального количества спустя 1ч получается 2,6г. фермента. Пусть Q-наличие фермента (г.) в момент времени t (ч.), то скорость прироста фермента При t=0, Q=2г., тогда С=ln2, получим При t=1, Q=2,6, тогда к=ln1,3 При t=4, Q= Вопросы для самопроверки
Задания для самостоятельного решения Задание № 1. Проверить, является ли заданная функция решением данного дифференциального уравнения.
Задание № 2. Р ешить обыкновенное дифференциальное уравнение первого порядка.
Задание № 3. Р ешить задачу Коши.
Задание № 4. Р ешить дифференциальное уравнение с разделяющимися переменными.
Задание № 5. Найти частное решение дифференциального уравнения с разделяющимися переменными.
Задание № 6. 1. Найти закон движения тела по оси Оу, если оно начало двигаться из точки M (0; 6) со скоростью v = 4t – 6t2.
2. Составить уравнение кривой, проходящей через точку М(2, -1) и имеющей касательную с угловым коэффициентом k = 1/(2y). 3. Найдите уравнение кривой, проходящей через точку N (3, 4), если угловой коэффициент касательной равен – x/y. 4. Найти кривые, для которых угловые коэффициенты касательных в каждой точке равны 2х-1. Выделить кривую, проходящую через точку А(1;1). 5. Найти кривые, для которых угловой коэффициент касательной в каждой точке на любой из этих кривых равен квадрату абсциссы точки касания. Выделить кривую, проходящую через точку А(-3;-1). 6. Определить путь, который пройдет автомобиль за время t=10 с, если его скорость пропорциональна пути и если за 2с автомобиль проходит 10м, а за 5с- 50м. 7. При брожении скорость прироста действующего фермента пропорциональна его первоначальному содержанию. Определить содержание фермента через 6ч. после брожения, если вместо 5г. первоначального количества спустя 1ч, получается 6г. фермента. V. Основы дискретной математики Основные понятия теории множеств Понятие множества Совокупность объектов, объединенных некоторым признаком, свойством, составляет понятие множество. Рассмотрим некоторые примеры множеств: 1. множество студентов в группе 2. множество книг на полке 3. множество людей в мире 4. множество действительных чисел Определение. Объекты, составляющие множество, называются его элементами. Множества обозначаются прописными буквами латинского алфавита A, B, C, …, а элементы множеств – строчными a, b, c, …. Запись a Запись b Определение. Множество, состоящее из конечного числа элементов, называется конечным, из бесконечного числа элементов – бесконечным.
Определение. Если каждый элемент множества A есть элемент множества B, то говорят, что A есть подмножество множества B, и пишут A Определение. Если A Пример. Определение. Множество А равно множеству В, если A Если множества А и В – конечны, то в случае равенства они состоят из одних и тех же элементов. 2) Способы задания множеств Существует три способа задания множеств. 1. Перечислением его элементов: 2. Описанием характеристических свойств, которыми обладают его элементы. Пример. 3. Порождающей процедурой, которая описывает способ получения элементов множества из уже имеющихся элементов либо других объектов. В этом случае элементами множества являются все объекты, которые могут быть построены с помощью такой процедуры. Пример. Задать с помощью порождающей процедуры множество N всех натуральных чисел: 1, 2, 3, …. Решение. В данном случае порождающая процедура содержит два правила: а) 1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 196; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.228 (0.072 с.) |
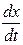 будет скоростью размножения этих бактерий. Так как скорость размножения
будет скоростью размножения этих бактерий. Так как скорость размножения 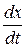 пропорциональна количеству бактерий, то существует постоянная k такая, что
пропорциональна количеству бактерий, то существует постоянная k такая, что 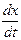 = kx.
= kx. = С∙ ekt ∙ k = k(Cekt) = kx.
= С∙ ekt ∙ k = k(Cekt) = kx.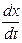 = - kx(t)называется дифференциальным уравнением радиоактивного распада.
= - kx(t)называется дифференциальным уравнением радиоактивного распада.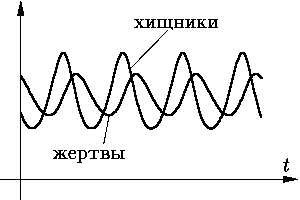 описывающая такую популяцию хищник — жертва и называется моделью Лотки — Вольтерры.
описывающая такую популяцию хищник — жертва и называется моделью Лотки — Вольтерры.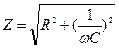
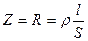 , где
, где 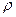 = 1,5 Ом . м – удельное сопротивление крови, R – омическое сопротивление участка кровеносного русла.
= 1,5 Ом . м – удельное сопротивление крови, R – омическое сопротивление участка кровеносного русла.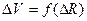 .
.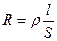 умножаем числитель и знаменатель на
умножаем числитель и знаменатель на 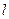 – длина сосуда.
– длина сосуда.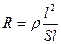 (
(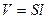 );
); 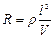 ;
; 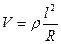
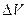 продифференцируем левую и правую часть уравнения
продифференцируем левую и правую часть уравнения 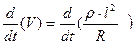
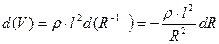
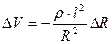 – основная формула реографии, где
– основная формула реографии, где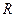 – базовое сопротивление участка ткани, на который накладывают электроды;
– базовое сопротивление участка ткани, на который накладывают электроды;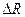 – максимальное изменение сопротивления участка кровеносного русла за один сердечный цикл.
– максимальное изменение сопротивления участка кровеносного русла за один сердечный цикл.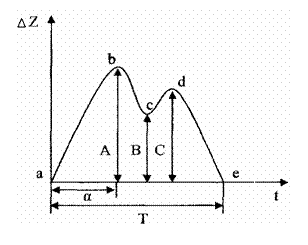 ab – анакрота;
ab – анакрота;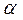 – длительность анакроты (характеризует тонус и эластичность артерий);
– длительность анакроты (характеризует тонус и эластичность артерий);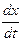 ; тогда
; тогда 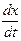 = 2 t + 3 t2.
= 2 t + 3 t2.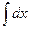 =
= 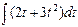
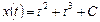 – общее решение дифференциального уравнения.
– общее решение дифференциального уравнения.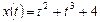
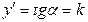 , где k – угловой коэффициент касательной к графику функции. Получим:
, где k – угловой коэффициент касательной к графику функции. Получим: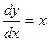 ,
, 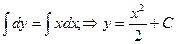 .
.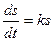 , где к- коэффициент пропорциональности.
, где к- коэффициент пропорциональности.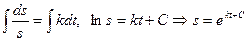

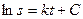 примет вид:
примет вид: 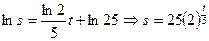 .
.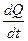 . По условию задачи
. По условию задачи 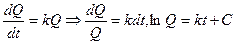 .
.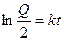 .
.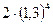 =5,7гр.
=5,7гр.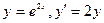
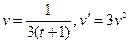
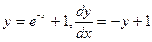
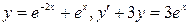
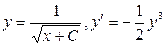
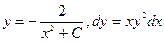
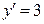
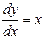
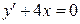
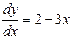
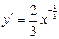
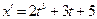
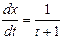
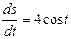
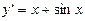
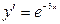

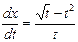
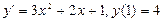
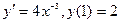
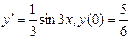
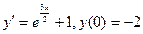
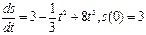
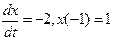
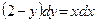
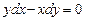
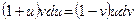
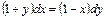

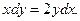
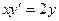
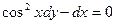
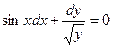
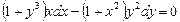
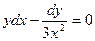 при х=0, у=1
при х=0, у=1
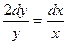 при х=1, у=
при х=1, у= 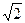
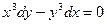 при х=1, у=2
при х=1, у=2
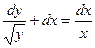 при х=1, у=1
при х=1, у=1
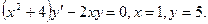
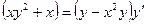 ,х=2,
у = 1
,х=2,
у = 1
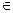 M означает, что элемент a принадлежит множеству M.
M означает, что элемент a принадлежит множеству M.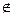 M означает, что элемент b не принадлежит множеству M.
M означает, что элемент b не принадлежит множеству M. Определение. Множество, не содержащее элементов, называется пустым и обозначается .
Определение. Множество, не содержащее элементов, называется пустым и обозначается .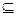 В. Если A
В. Если A 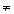 В, то А называется строгим подмножеством и обозначается A
В, то А называется строгим подмножеством и обозначается A 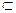 В
В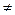 В, то A называется строгим (собственным) подмножеством и обозначают A
В, то A называется строгим (собственным) подмножеством и обозначают A 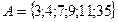 ,
, 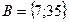 . Имеем В
. Имеем В 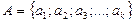
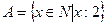 - множество натуральных чисел, делящихся на 2.
- множество натуральных чисел, делящихся на 2.


