
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обобщенный гармонический ряд (ряд Дирихле)
сходится, если Признак Даламбера. Если члены ряда
то при при при Радикальный признак Коши. Если члены ряда
то при при при
Чтобы исследовать сходимость ряда с положительными членами
где Un содержит произведения многих сомножителей (например, факториалы) необходимо выполнить следующие действия.. Если при вычислении предела
можно сократить множители в числителе и знаменателе дроби 1. Проверим, что Un>0 при всех 2. Найдем 3. Вычислим предел 4. Применим признак Даламбера. Пример.Исследовать сходимость ряда 1. Проверим, что члены ряда положительны. Действительно,
при всех 2. Найдем
3. Вычислим предел
4. Применим признак Даламбера. Так как k=0<1, то ряд Пример. Исследовать на сходимость ряд
1. Проверим, что члены ряда положительны. Действительно,
при всех 2. Найдем
3.Вычислим предел
4. Применим признак Даламбера. Так как 5. Используем необходимый признак сходимости ряда
Т.е. не выполняется необходимое условие сходимости ряда, делаем вывод, что предложенный ряд Пример. Исследовать на сходимость ряд
1. Проверим, что члены ряда положительны. Действительно,
при всех 2. Найдем
3.Вычислим предел
4. Применим признак Даламбера. Так как
Чтобы исследовать сходимость ряда с положительными членами
где Если
1. Проверим, что Un>0 при всех 2. Вычислим предел 3. Применим радикальный признак Коши. Замечание. Полезно иметь в виду, что
где P(n) – многочлен относительно n. Пример.Исследовать сходимость ряда
Общий член ряда имеет вид 1 способ. 1. Проверим, что члены ряда положительны. Действительно,
при всех 2. Вычислим предел
3. Применим радикальный признак Коши. Так как
расходится. 2 способ. Нарушается необходимый признак сходимости ряда
а не ноль. Следовательно, ряд Знакочередующиеся ряды. Определение. Ряд вида где Исследование сходимости таких рядов проводится на основании теоремы Лейбница – достаточного признака сходимости знакочередующегося ряда. Теорема (Лейбница) Знакочередующийся ряд 1) его члены монотонно убывают по абсолютной величине, т.е.
2) его общий член Un стремится к нулю при
Замечание. Сумма такого ряда положительна и не превосходит первого члена ряда По знакочередующемуся ряду
|
|||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 116; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.86.134 (0.012 с.) |
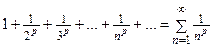
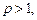 и расходится, если
и расходится, если 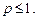
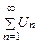 положительны и существует предел
положительны и существует предел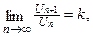
 ряд сходится;
ряд сходится;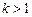 ряд расходится;
ряд расходится;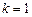 вопрос о том, сходится ряд или расходится, не решен и требуется дополнительное исследование с помощью других достаточных признаков сходимости.
вопрос о том, сходится ряд или расходится, не решен и требуется дополнительное исследование с помощью других достаточных признаков сходимости.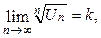
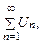
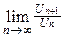
 , то обычно применяют признак Даламбера.
, то обычно применяют признак Даламбера.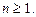
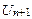 . Для этого в формуле определения общего члена ряда Un заменим n на n+1.
. Для этого в формуле определения общего члена ряда Un заменим n на n+1.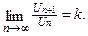
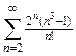 .
.

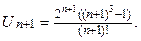
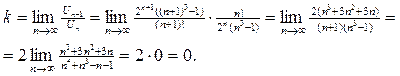
 сходится.
сходится.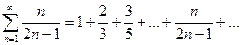

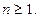
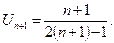
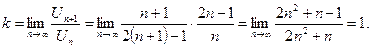

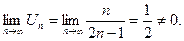
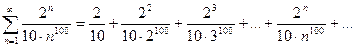
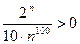
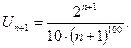
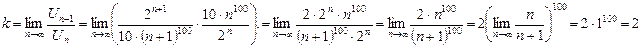
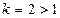 , то ряд
, то ряд 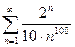 расходится.
расходится.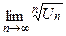 существует и легко вычисляется необходимо выполнить следующие действия.
существует и легко вычисляется необходимо выполнить следующие действия.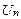 имеет, например, вид
имеет, например, вид 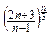 или
или 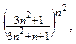 то
то 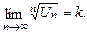
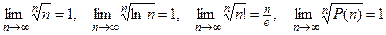 ,
,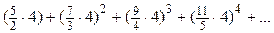
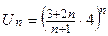 , где
, где 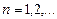
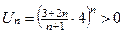

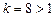 , то ряд
, то ряд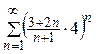
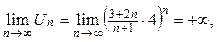
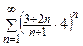 расходится.
расходится. =
= 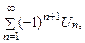
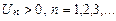 и два любых соседних члена имеют противоположные знаки, называется знакочередующимся.
и два любых соседних члена имеют противоположные знаки, называется знакочередующимся.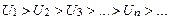 и
и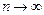 , т.е.
, т.е.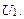
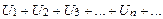 =
= 


