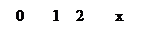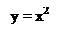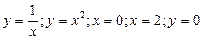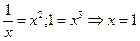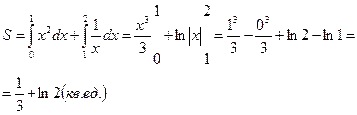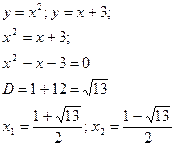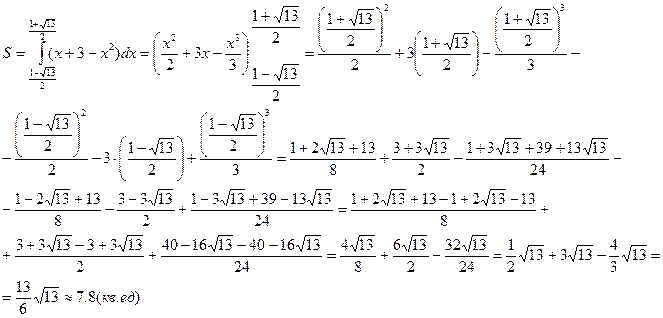Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства определенного интеграла.
1. 2. 3. 4. 5. Если f(x) £ j(x) на отрезке [ a, b] a < b, то 6. Вычисление определенных интегралов через предел интегральных сумм связано с большими трудностями. Поэтому существует другой метод, основанный на тесной связи, существующей между понятиями определенного и неопределенного интегралов. Теорема. Если функция y = f(x) непрерывна на отрезке [ a, b] и F(x) – какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:
которая называется формулой Ньютона–Лейбница. Нахождение определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два этапа: на первом этапе находят некоторую первообразную F(x) для подынтегральной функции f(x); на втором – находится разность
1) 2) Вычисление площади фигуры с помощью определённого интеграла. Наиболее простая геометрическая задача: S = S = где S – площадь криволинейной трапеции, ограниченной графиком функции y= f(x), отрезком [ a, b] на оси Ох и прямыми x= a и x= b,(a< b).
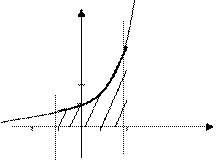
Пример:
При построении графиков функций, могут получиться следующие случаи:
1. Площадь фигуры, ограниченной линиями: y = f (x); y = 0; x = a; x = b.
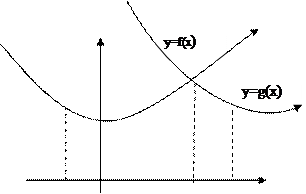
2. Площадь фигуры, ограниченной линиями: y = f (x); y = g (x); y = 0, x = a; x = b.
3. Площадь фигуры, ограниченной линиями: y = f (x); y = 0; x = a; x = b
4. Площадь фигуры, ограниченной линиями: y = f (x); y = g (x)
Пример: 1)
Найдём из уравнения
Пример:
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 68; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.228 (0.009 с.) |
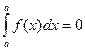 - интеграл с одинаковыми пределами интегрирования равен нулю.
- интеграл с одинаковыми пределами интегрирования равен нулю.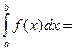 -
-  - перестановка пределов интегрирования приводит к изменению знака.
- перестановка пределов интегрирования приводит к изменению знака.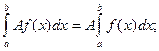 - постоянный множитель можно выносить за знак интеграла.
- постоянный множитель можно выносить за знак интеграла.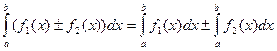 - интеграл от алгебраической суммы функций равен такой же сумме интегралов от этих функций (свойство линейности).
- интеграл от алгебраической суммы функций равен такой же сумме интегралов от этих функций (свойство линейности).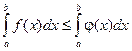 .
.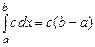 - иинтеграл от постоянной величины равен этой постоянной, умноженной на длину отрезка интегрирования.
- иинтеграл от постоянной величины равен этой постоянной, умноженной на длину отрезка интегрирования.
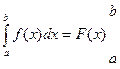
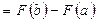
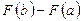 значений этой первообразной на концах отрезка [ a, b].
значений этой первообразной на концах отрезка [ a, b]. Пример. Вычислить определенный интеграл.
Пример. Вычислить определенный интеграл.
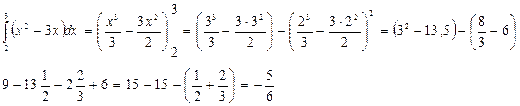
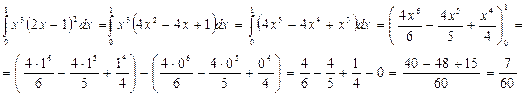
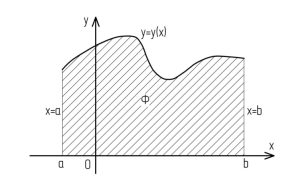
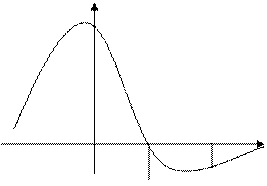
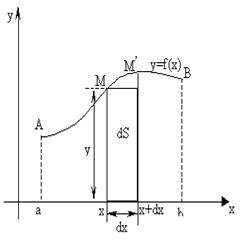 найти площадь фигуры, границы которой определены уравнениями соответствующих линий и осью OX. В этом случае рассматривается криволинейная трапеция, о которой говорилось выше (рис. 1.) и используется геометрический смысл определенного интеграла как предел суммы площадей маленьких прямоугольников, образующих ступенчатую фигуру. Элементом площади в прямоугольной декартовой системе координат, полученным в процессе построения интегральной суммы, в этом случае служит прямоугольник площадь которого
найти площадь фигуры, границы которой определены уравнениями соответствующих линий и осью OX. В этом случае рассматривается криволинейная трапеция, о которой говорилось выше (рис. 1.) и используется геометрический смысл определенного интеграла как предел суммы площадей маленьких прямоугольников, образующих ступенчатую фигуру. Элементом площади в прямоугольной декартовой системе координат, полученным в процессе построения интегральной суммы, в этом случае служит прямоугольник площадь которого 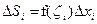 , Тогда площадь криволинейной трапеции находится по формуле
, Тогда площадь криволинейной трапеции находится по формуле 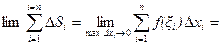
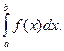
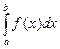

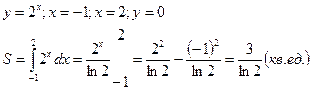
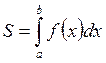
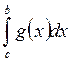
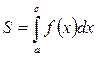
 y
a b
x
y
a b
x
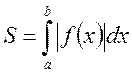
 y
y=f(x)
a b x
y
y=f(x)
a b x
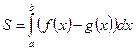


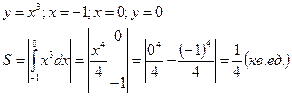

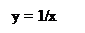
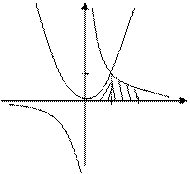 Пример:
Пример: