
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обыкновенные дифференциальные уравнения.
Пусть x − независимая переменная, y = y (x) − искомая неизвестная функция. Дифференциальное уравнение – основной математический аппарат в естествознании. Они применяются в физике, астрономии, аэродинамике и теории упругости, химии, экономике, биологии и медицине. Такой подход к изучению явлений природы впервые был предложен итальянским ученным Г. Галилеем. Впервые его блестяще применил один из создателей математического анализа И. Ньютон. Решение задач методом математического моделирования сводится к отысканию неизвестной функции из уравнения, содержащего независимую переменную, искомую функцию и производные этой функции. Пусть x − независимая переменная, y = y(x) − искомая неизвестная функция. Определение. Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию y и ее производные или дифференциалы. Символически дифференциальное уравнение записывается так:
Например, уравнения Определение. Порядком дифференциального уравнения называется наибольший порядок производных, входящих в данное уравнение. y + xy /=0 – дифференциальное уравнение 1-го прядка
Определение. Решением дифференциального уравнения называется всякая функция, которая обращает данное уравнение в тождество. Существуют задачи, приводящие к дифференциальным уравнениям. Рассмотрим одну из них. Размножение бактерий. На опытах с бактериями установлено, что скорость размножения бактерий пропорциональна их количеству, если, конечно, для них имеется достаточный запас пищи. Так как сами бактерии очень малы, а их количество велико, то можно считать, что масса бактерий с течением времени меняется непрерывно. Тогда скорость прироста массы бактерий называется скоростью размножения. Если через число x(t) обозначить массу всех бактерий в момент времени t, то
По условию x(t) и x/(t) неотрицательные, поэтому коэффициент k тоже неотрицательный.
Уравнение (1) является простейшим примером дифференциального уравнения. Оно называется дифференциальным уравнением размножения. Искомым неизвестным уравнения (1) является функция x = x(t), которая в уравнение входит вместе со своей производной. Решением данного уравнения является функция вида x = Cekt, где С – const. Действительно,
Радиоактивный распад. Опытом установлено, что скорость распада радия в каждый момент времени пропорциональна начальному количеству радия. Таким образом, если через x(t) обозначить массу вещества, еще не распавшегося к моменту времени t, то скорость распада Уравнение Определение. Дифференциальное уравнение называется обыкновенным, если в нем одна независимая переменная. Основная задача интегрального исчисления – отыскание функции y, производная которой равна данной непрерывной функции f(x), - сводится к простейшему дифференциальному уравнению y / = f(x). Общее решение этого уравнения есть
где С – произвольная постоянная, а под интегралом понимается одна из первообразных функции f(x). Определение. Общим решением дифференциального уравнения 1-го порядка y / = f(x,у) в области D называется функция y = φ(x, С), обладающая следующими свойствами: 1) она является решением данного уравнения при любых действительных значениях произвольной постоянной С; 2) для любого начального условия y(x0) = y0 такого, что (x0, y0) 3) Всякое решение y = φ(x, С0), получающееся из общего решения y = φ(x, С) при конкретном значении С = С0, называется его частным решением. Пример. Решить уравнение
Интегрируя, обе части уравнения, получим: x (t) = Определение. Задача, в которой требуется найти частное решение уравнения y / = f(x,у), удовлетворяющее начальному условию y(x0) = y0, называется задачей Коши.
Пример. 1) Решите задачу Коши
Интегрируя, обе части уравнения, получим:
Используя, начальные условия, найдем С.
-3+С = 6 С = 9 Таким образом, 2) Является ли функция Так как функция В уравнение входит производная функции y, найдем ее: Подставим найденное значение производной и значение самой функции в исходное уравнение:
Таким образом, 3) Является ли функция Найдем производную функции
Подставим найденное значение dy и значение самой функции в уравнение:
Так как 0 = 0 следовательно, функция 4) Найти решение задачи Коши: Найдем общее решение данного дифференциального уравнения:
где С – произвольная постоянная. Пользуясь начальным условием, имеем y(1) = 12 + 1 + C = 3. Следовательно С = 1, и искомое решение будет иметь вид 5) Найти решение задачи Коши: Найдем общее решение данного дифференциального уравнения:
где С – произвольная постоянная. Пользуясь начальным условием, имеем x(1) = 13 -2 ln1 + 5 ∙1 + C = 2 → 6 + C = 2 → C = - 4. Следовательно, искомое решение имеет вид:
|
||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 162; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.147.190 (0.014 с.) |
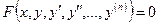
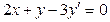 ,
, 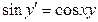 ,
,  являются дифференциальными уравнениями.
являются дифференциальными уравнениями.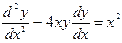 - дифференциальное уравнение 2-го порядка
- дифференциальное уравнение 2-го порядка - уравнение n -го порядка
- уравнение n -го порядка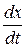 будет скоростью размножения этих бактерий. Так как скорость размножения
будет скоростью размножения этих бактерий. Так как скорость размножения  = С∙ ekt ∙ k = k(Cekt) = kx.
= С∙ ekt ∙ k = k(Cekt) = kx.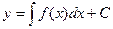
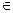 D, существует единственное значение С = С0, при котором решение y = φ(x, С) удовлетворяет заданному начальному условию.
D, существует единственное значение С = С0, при котором решение y = φ(x, С) удовлетворяет заданному начальному условию.
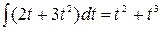 + C – общее решение дифференциального уравнения.
+ C – общее решение дифференциального уравнения. - 3 x2 - 6 x + 7 = 0, y (1) = 6.
- 3 x2 - 6 x + 7 = 0, y (1) = 6.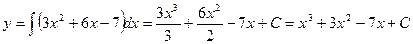
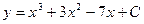 - общее решение дифференциального уравнения.
- общее решение дифференциального уравнения.
 - частное решение дифференциального уравнения.
- частное решение дифференциального уравнения.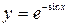 решением дифференциального уравнения
решением дифференциального уравнения 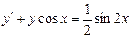 .
.
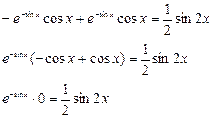
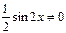 , следовательно, функция
, следовательно, функция 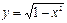 решением дифференциального уравнения
решением дифференциального уравнения 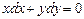 .
. :
: .
.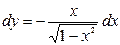
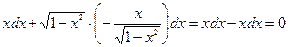
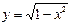 является решением дифференциального уравнения
является решением дифференциального уравнения 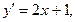 y(1) = 3
y(1) = 3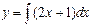 ,
,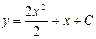
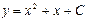
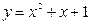 .
.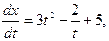 x(1) = 2
x(1) = 2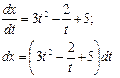
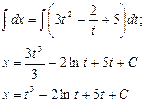
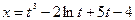 .
.


