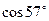Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение дифференциала для приближенных вычислений.
Дифференциал функции применяется при решении многих математических задач. Рассмотрим два типа задач, которые возможно рационально решить, используя понятия дифференциал. Кроме, того, мы применим дифференциал функции при решении задач профессиональной направленности. Рассмотрим первый тип задач. 1. Приближенные вычисления значения функции в заданной точке. Воспользуемся формулой для приближенных вычислений значения функции
Преобразуем выражение, перенесем Покажем на примере: Пример. Вычислить значение функции Для удобства счета выберем вблизи заданной точки Затем найдем дифференциал функции: И, учитывая, что Итак, приближенное значение данной функции в точке Рассмотрим второй тип задач. 2. Вычисление приращения функции в заданной точке. Из формулы приближенного вычисления значения функции получим:
Пример. Найти приращение функции
Пример. Предприниматель Рыбкин разводит радужную форель в своем рыбхозяйстве. Статистическим путем за годы работы он сделал вывод, что численность популяций в зависимости от времени для данных условий разведения определяется формулой Решение: Известно:
Вывод: За 4 года работы рыбхозяйства численность популяции увеличилась на 7784 единицы. Пример. Вычислить приближенное значение приращения функции При изменении аргумента от х = 1 до х = 1,001 Находим дифференциал аргумента:
Пример. Найти приближенное значение
Тогда
Пример. Найти приближенное значение ln 0,97
Пример. Найти приближенное значение
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
Задания для самостоятельного решения Задание № 1. Найти производную функции.
Задание № 2. Найти вторую производную функции. 1. Найти ускорение тела, движущегося по закону s (t) = 2 t 3 + 5 t 2 + 4 t (s — путь в метрах, t — время в минутах), в момент времени: a) t = 40 сек; б) t = 1 ч. 2. Найти ускорение тела, движущегося по закону s = √ t (s — путь в метрах, t — время в минутах), в произвольный момент времени t. 3. Для данных функций найти производные всех порядков.
4. Доказать, что для функции у = a sin x + b cos х справедливо соотношение y IV= у. 5. Сколько раз нужно продифференцировать функцию у = (х 2 + 1)100, чтобы в результате получился многочлен 50-й степени? 6. Найти производную 100-го порядка от функции у = sin х cos2 х. 7. Заполнить таблицу.
Задание № 3. Найти производную сложной функции.
Задание № 4. Исследовать функцию и построить ее график. Задание № 5. Найти наибольшее и наименьшее значения функции на отрезке.
Задание № 6. Найти дифференциал функции.
Задание № 7. Применение дифференциала функции для приближенных вычислений.
1. Вычислить значение функции 2. Найти приращение функции 3. Вычислить приближенное значение приращения функции 4. Найти приближенное значение 5. Найти приближенное значение arctg 1,02 6. Найти приближенное значение
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 602; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.160.61 (0.012 с.) |

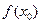 в левую часть, получим:
в левую часть, получим:  . Правая часть есть дифференциал функции. Значит, чтобы найти значение функции в заданной точке, необходимо воспользоваться формулой
. Правая часть есть дифференциал функции. Значит, чтобы найти значение функции в заданной точке, необходимо воспользоваться формулой 
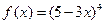 в точке
в точке 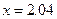 .
.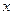 точку
точку  . Тогда приращение аргумента будет равно
. Тогда приращение аргумента будет равно 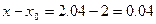 ,
,  . Вычислим значение функции в точке
. Вычислим значение функции в точке 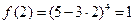 .
. .
. вычислим его в точке
вычислим его в точке 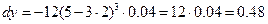 .
. . Обратите внимание, что без калькулятора вычислить чему равно значение функции в точке 2.04 довольно сложно, так как здесь высокая степень многочлена. А используя дифференциал, мы вычислили устно приближенное значение функции. Такие расчеты также рационально использовать в физике.
. Обратите внимание, что без калькулятора вычислить чему равно значение функции в точке 2.04 довольно сложно, так как здесь высокая степень многочлена. А используя дифференциал, мы вычислили устно приближенное значение функции. Такие расчеты также рационально использовать в физике.
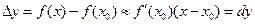 . Значит
. Значит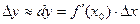
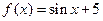 в точке
в точке  и при приращении
и при приращении 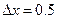 .
.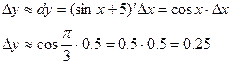
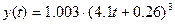 . Определить изменение численности популяции форели с 3-го года и до 7 лет работы рыбхозяйства.
. Определить изменение численности популяции форели с 3-го года и до 7 лет работы рыбхозяйства.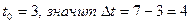 ,
,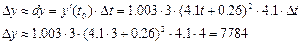
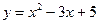
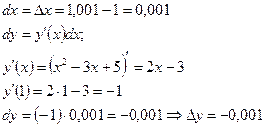
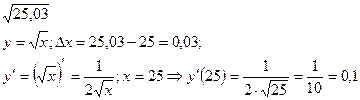

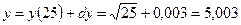
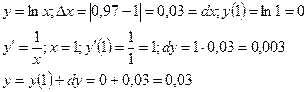

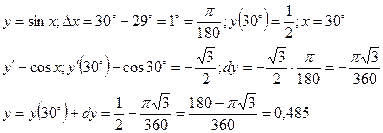

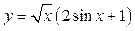
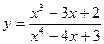


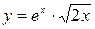
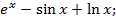
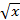 -
- 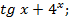
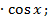
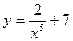

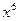



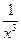
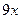

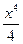
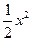

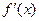
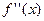
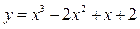 ;
;
 .
.
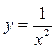 ;
;
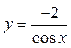 .
.
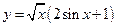 ;
;
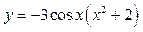 ;
;
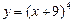
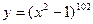


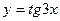


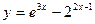

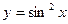
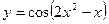
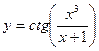
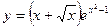
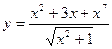
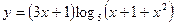
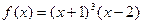
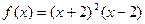
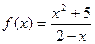
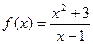
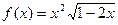
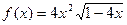
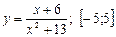
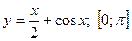
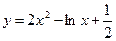 ;
; 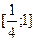
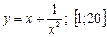
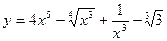

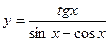

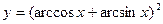
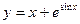
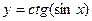
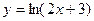
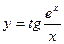

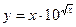

 в точке
в точке 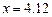 .
.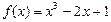 в точке
в точке 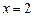 и при приращении
и при приращении 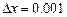 .
.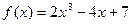 , при изменении аргумента от х = 2 до х = 2,002
, при изменении аргумента от х = 2 до х = 2,002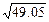 ,
,  .
.