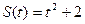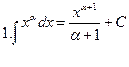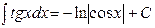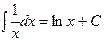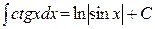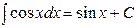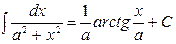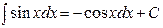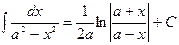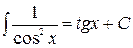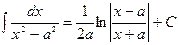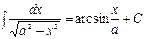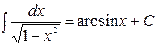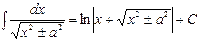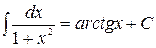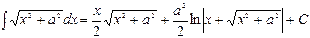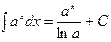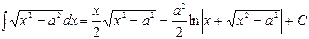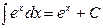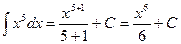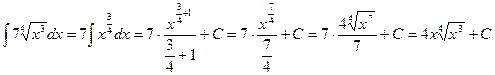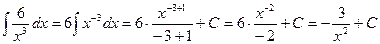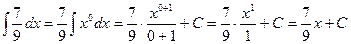Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
III. Интеграл и его Приложения
Нахождение производной имеет большое практическое значение. Однако, часто приходится решать обратную задачу: по известной производной отыскивать функцию, от которой найдена эта производная, т.е. выполнять действия, обратные дифференцированию. Это действие называется интегрированием. Неопределенный интеграл Пример. Известно, что производная от некоторой функции F(x) равна 4 x3: Решением этой задачи является функция x4, так как Определение. Функция F(x) называется первообразной для f(x) на некотором промежутке, если для всех х из этого промежутка Теорема. Если F(x) является первообразной для f(x) на некотором промежутке, то "С Î R j(x) = F(x) + C также является первообразной для f(x) на этом промежутке и других первообразных f(x) на этом промежутке не имеет. Доказательство. 1) "xÎI j’(x) = F’(x) + C‘ = F’(x) = f(x), то есть, j(x) – первообразная для f(x) на I. 2) Пусть j(x) – первообразная для f(x) на I, то есть, "xÎI j’(x) = f(x). Рассмотрим G(x) = j(x) – F(x), тогда "xÎI G’(x) = j’(x) – F’(x) = 0 Û G(x) = C Û j(x) = F(x) + C, ч. т. д. Определение. Множество всех первообразных функции f(x) называется неопределенным интегралом этой функции. Таким образом, В этом случае: Операция замены левой части этого равенства на правую называется интегрированием функции f(x). Пример.
Остановимся на практическом применении понятия неопределенного интеграла. Как известно, скорость движения тела представляет собой производную от пути по времени, т.е. V = S/(t), где S(t) – путь, пройденный телом к моменту времени t. Таким образом, если известен путь тела, то его скорость отыскивается с помощью операции дифференцирования. Рассмотрим теперь обратную задачу. Дана скорость тела V = V(t) как некоторая функция от времени. Нужно найти путь S(t). В задаче требуется найти функцию S(t), производная от которой равна V(t), т.е. Таким образом, если известна скорость тела, то его путь отыскивается с помощью операции интегрирования. Пример. Пусть
Таблица основных интегралов
Пример. Найти интегралы. 1) 2) 3) 4)
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 65; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.70.101 (0.008 с.) |
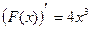 . Нужно найти функцию F(x).
. Нужно найти функцию F(x).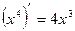 . Следовательно, F(x)= x4
. Следовательно, F(x)= x4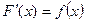 .
.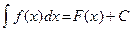 , где СÎR.
, где СÎR.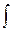 – знак интеграла; f(x) – подынтегральная функция; x – переменная интегрирования; F(x) – одна из первообразных функции f(x); С – постоянная интегрирования.
– знак интеграла; f(x) – подынтегральная функция; x – переменная интегрирования; F(x) – одна из первообразных функции f(x); С – постоянная интегрирования.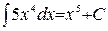 , где СÎR.
, где СÎR.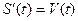 .
.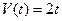 . Тогда
. Тогда 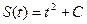 , так как
, так как 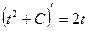 . Следовательно, выражение для пути
. Следовательно, выражение для пути