
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точки разрыва и их классификация.
Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной. Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.
х0
х0
Определение. Точка х0 называется точкой разрывафункции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке. Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее. Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва. Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен. Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) – немецкий математик, член- корреспондент Петербургской АН 1837г)
является непрерывной в любой точке х0. Пример. Функция f(x) =
Пример. f(x) = Функция не определена в точке х = 0, но имеет в ней конечный предел
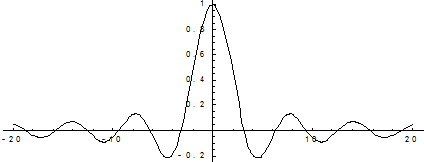
График этой функции:
1
0 x В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1 – го рода. Если доопределить функцию в точке х = 0, положив f(0) = 1, то функция будет непрерывна справа, если положить f(0) = -1, то функция будет непрерывной слева, если положить f(x) равное какому- либо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях тем не менее будет иметь в точке х = 0 разрыв 1 – го рода. В этом примере точка разрыва 1 – го рода не является устранимой. Таким образом, для того, чтобы точка разрыва 1 – го рода была устранимой, необходимо, чтобы односторонние пределы справа и слева были конечны и равны, а функция была бы в этой точке не определена. Асимптоты графика функции. Определение. Асимптотой графика функции y = f(x) называется прямая, обладающая свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные x= a, горизонтальные y= b, наклонные y= kx+ b.
Нахождение асимптот графика функции основано на следующих утверждениях. а) Вертикальные асимптоты График функции y = f (x) при
при этом x = a точка разрыва II рода. б) Горизонтальные асимптоты Пусть функция y = f(x) определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции Может случиться, что в) Наклонные асимптоты Пусть функция y = f(x) определена при значениях аргумента, достаточно больших по абсолютной величине, и существуют конечные пределы
Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет. Наклонная асимптота так же, как и горизонтальная, может быть односторонней. Пример. 1) Найти асимптоты кривой Функция определена при Найдем ее односторонние пределы в точке x=0. Так как Вычислим Вычислим Найдем
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ 1. Дайте определение предела функции точке. 2. Дайте определение предела функции на бесконечности. 3. Сформулируйте основные теоремы о пределах функций. 4. Дайте определение бесконечно малой функции. 5. Дайте определение бесконечно большой функции. 6. В чем заключается связь бесконечно больших и бесконечно малых функций? 7. Дайте определение непрерывности функции в точке. 8. Приведите примеры функций непрерывных в точке. 9. Дайте определение непрерывности функции на интервале. 10. Что такое точка разрыва? Точки разрыва первого и второго рода. 11. Приведите примеры точек разрыва первого и второго рода. 12. Что называется асимптотой функции? 13. Сформулируйте правило нахождения вертикальной асимптоты? 14. Сформулируйте правило нахождения горизонтальной асимптоты? 15. Сформулируйте правило нахождения наклонной асимптоты? Задания для самостоятельного решения Задание № 1. Вычислить пределы функций.
Задание № 2. Исследовать функцию на непрерывность.
Задание № 3. Найти точки разрыва функции и определить их род.
Задание № 4. Найти асимптоты графика функции.
II. ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ 1. Понятие производной функции. Формулы дифференцирования.
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 127; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.162.216 (0.019 с.) |
 Если односторонний предел
Если односторонний предел 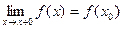 , то функция называется непрерывной справа.
, то функция называется непрерывной справа.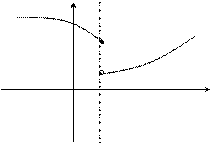 Если односторонний предел
Если односторонний предел 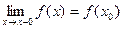 , то функция называется непрерывной слева.
, то функция называется непрерывной слева.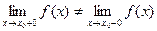
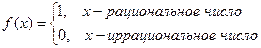
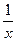 имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к.
имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к.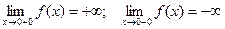 .
.
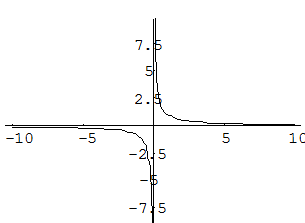
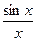
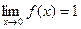 , т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:
, т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию: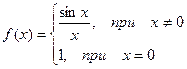
 Пример. f(x) =
Пример. f(x) = 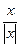 =
= 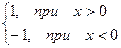
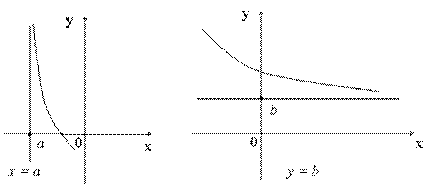
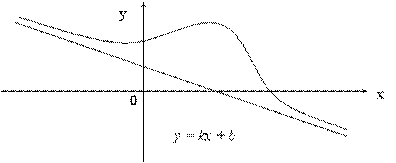
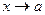 имеет вертикальную асимптоту, если
имеет вертикальную асимптоту, если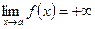 или
или 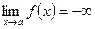 ,
, . Тогда прямая y= b есть горизонтальная асимптота графика функции y = f(x).
. Тогда прямая y= b есть горизонтальная асимптота графика функции y = f(x).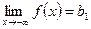 , а
, а 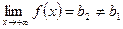 , причем
, причем 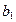 и
и 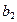 - конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов
- конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов 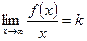 и
и  . Тогда прямая y= kx+ b является наклонной асимптотой графика функции y = f(x).
. Тогда прямая y= kx+ b является наклонной асимптотой графика функции y = f(x).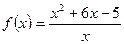 .
.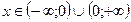 , следовательно x=0 – точка разрыва.
, следовательно x=0 – точка разрыва.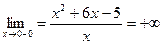 и
и 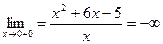 , то x=0 – вертикальная асимптота.
, то x=0 – вертикальная асимптота.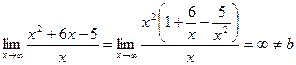 . Горизонтальных асимптот нет.
. Горизонтальных асимптот нет. . Таким образом, k = 1.
. Таким образом, k = 1.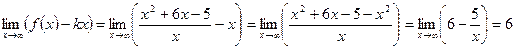 Таким образом, b = 6 и y = x + 6 – наклонная асимптота.
Таким образом, b = 6 и y = x + 6 – наклонная асимптота.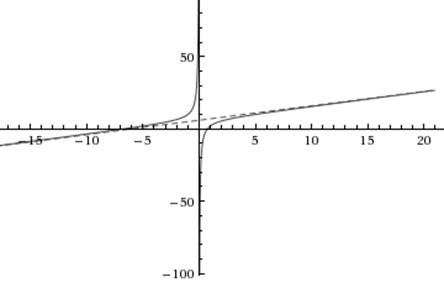
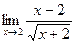
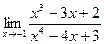
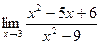

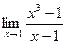
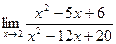
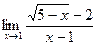
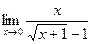
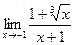
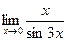
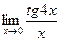
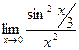
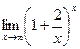
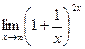
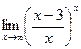
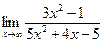
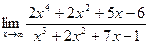
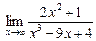
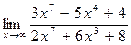
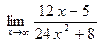
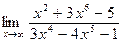
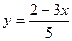
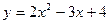
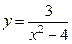
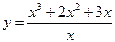
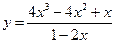
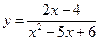
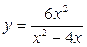

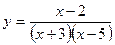
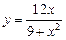

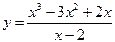
 Понятие производной является одним из основных математических понятий. Производная широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости разных процессов.
Понятие производной является одним из основных математических понятий. Производная широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости разных процессов.


