Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции над множествами. Диаграммы Эйлера-Венна
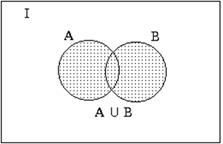
Определение. Универсальным множеством I называется множество всех элементов, которые могут встретиться в данном исследовании. Диаграмма Эйлера-Венна представляет собой изображение прямоугольника, обозначающего универсальное множество I, а внутри него – кругов, соответствующих рассматриваемым множествам. Фигуры должны быть соответствующим образом обозначены и могут схематически пересекаться или не пересекаться в случае, требуемом в задаче. Точки, лежащие внутри различных областей диаграммы, можно рассматривать как элементы соответствующих множеств. Заштриховав определенные области диаграммы, можно получать наглядное геометрическое представление требуемых в задаче множеств и их комбинаций. Определение. Объединением двух множеств A и B называется множество, состоящее из элементов, принадлежащих хотя бы одному из множеств A и B (обозначается
Для конечных множеств А и В справедливо равенство:
Определение. Пересечением двух множеств A и B называется множество, состоящее из элементов, принадлежащих и множеству A и множеству B (обозначается
Определение. Дополнением (до I) множества A называется множество всех элементов, не принадлежащих А (но принадлежащих I) (обозначается
Определение. Разностью множеств A и B называется множество тех элементов множества А, которые не содержатся в множестве В (обозначается
Определение. Симметрической разностью множеств A и B называется объединение множеств

Свойства операций над множествами 1. 2. 3. 4. 5. 6. 7. Для любого множества X 8. Для любых двух множеств X и Y справедливо: если X Примеры решения задач Пример 1. Задать различными способами множество М всех четных чисел 2, 4, 6, …, не превышающих 100. Решение. 1. Задание списком: 2. Порождающая процедура:
- 2 - если n - n 3. Описание характеристических свойств: Пример 2. Какие из приведенных определений множеств A, B, C, D являются корректными: а) б) Принадлежит ли число 1 множеству D? Решение. а) Определение множества б) Пи пересечении элементов множества не следует указывать один и тот же элемент несколько раз. Корректное определение: в) Определение множества г) Определение списком множества Однако 1 Пример 3. Пусть универсальное множество I – множество всех сотрудников некоторой фирмы; A – множество всех сотрудников данной организации в возрасте старше 35 лет; В – множество сотрудников, имеющих стаж работы более 10 лет; С – множество менеджеров фирмы. Каков содержательный смысл (характеристическое свойство) каждого из следующих множеств: а) В; в) б) Решение. а) В – множество сотрудников, имеющих стаж работы более 10 лет; б) в) г) д) множество менеджеров со стажем работы не более 10 лет. Пример 4. Задать множества M, Решение. М – множество натуральных чисел, больших 100; Запись - это может быть множество всех отрицательных целых чисел; - это может быть множество всех положительных дробных чисел; - это может быть пустое множество чисел.
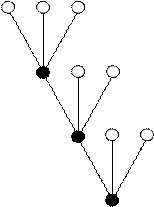
Пример 5. Осуществить операции над множествами Решение. а) б) в) г) д) Универсальное множество I не определено, поэтому, строго говоря, операции дополнения множества A и B не могут быть выполнены. Дополним условие. Пусть е) Пример 6. Пусть Найти а) Решение. а) б) в) г) Пример 6. Экзамен по математике сдавали 250 студентов, оценку ниже «5» получили 180 человек, а сдали этот экзамен 236 студентов. Сколько человек получили оценку «3» и «4»? Решение. Пусть А – множество студентов, сдавших экзамен, В – множество студентов, получивших оценку ниже «5». По условию (А) = 236, (В) = 180, По формуле 250 = 180 + 236 - Ответ: 166 человек получили оценку «3» и «4». Пример 7. В техникуме 1400 студентов. Из них 1250 умеют кататься на лыжах, 952 – на коньках. Ни на лыжах, ни на коньках не умеют кататься 60 учащихся. Сколько студентов умеют кататься и на лыжах и на коньках? Решение. Множество студентов техникума будем считать основным множеством I, А и В - соответственно множество студентов, умеющих кататься на лыжах и на коньках. Учащиеся, не умеющие кататься ни на лыжах, ни на коньках, составляют множество Согласно равенству Ответ: 862 студента умеют кататься и на лыжах и на коньках. Основы теории графов Разберем задачи, подводящие, учащихся к понятию графа, Задача 1 Герой произведения Н.В.Гоголя “Мертвые души” Плюшкин из экономии разрезает каждый лист бумаги на три части. Некоторые из полученных листов он также режет на три части и т.д. Сколько листков бумаги он получит, если разрежет k листов? Решение. Сделаем рисунок к условию задачи. При этом листы бумаги будем обозначать кружками: кружки, соответствующие разрезанным листам, закрасим; остальные оставим не закрашенными.
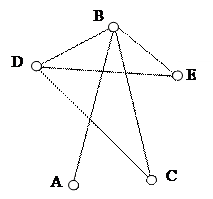
Рисунок помогает увидеть, что при разрезании появляются три новых листика вместо одного. Таким образом, получилось 1+2*1=3 листка; если разрезали два листа, то получилось 1+2*2=5 листков; если три, то - 1+2*3=7 и т.д. Если же было разрезано k листов, то образовалось 1+2k листиков. При решении задачи, мы получили схемы, похожие на ветку дерева с листьями. Задача 2 В соревнованиях по шашкам участвует шесть человек: Кирилл, Денис, Ольга, Сергей, Полина и Андрей. Соревнование проводится по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Кирилл сыграл с Денисом, Сергеем и Андреем; Денис, как уже говорилось, с Кириллом и еще с Сергеем; Ольга – с Сергеем, Полиной, Андреем; Сергей – с Кириллом, Денисом и Ольгой; Полина – с Ольгой, а Андрей – с Кириллом и Ольгой. Сколько игр проведено к настоящему моменту и сколько еще осталось? Решение.
Получили некоторую схему, из которой видно, что число игр, проведенных к настоящему моменту, равно количеству изображенных на ней отрезков, то есть семь.
Чтобы найти число игр, которые осталось провести, соединим пунктирной линией еще не игравших друг с другом участников.
Таких “пунктирных” отрезков получилось восемь, то есть нужно провести еще восемь игр. Кирилл должен сыграть с Ольгой и Полиной, Денис – с Ольгой, Полиной и Андреем и т.д. Есть ли что-нибудь общее у полученных схем? Да. Они все состоят из точек (кружков) и линий (прямых или кривых), соединяющих пары точек. Эти схемы являются представителями так называемых графов. Неформально граф можно рассматривать как множество точек и соединяющих эти точки линий со стрелками или без них. С графами, сами того не замечая, мы сталкиваемся постоянно. Например, графом является схема линий метрополитена. Точками на ней представлены станции, а линиями — пути движения поездов. Исследуя свою родословную и возводя ее к далекому предку, мы строим так называемое генеалогическое древо. И это древо — граф. Графы служат удобным средством описания связей между объектами. Но граф используют отнюдь не только как иллюстрацию. Например, рассматривая граф, изображающий сеть дорог между населенными пунктами, можно определить маршрут проезда от пункта А до пункта Б. Если таких маршрутов окажется несколько, хотелось бы выбрать в определенном смысле оптимальный, например самый короткий или самый безопасный. Для решения задачи выбора требуется проводить определенные вычисления над графами. При решении подобных задач удобно использовать алгебраическую технику, да и само понятие графа необходимо формализовать. Методы теории графов широко применяются в дискретной математике. Без них невозможно обойтись при анализе и синтезе различных дискретных преобразователей: функциональных блоков компьютеров, комплексов программ и т.д. Определение. Графом называется совокупность двух множеств: непустого множества точек (вершин) и множества линий, соединяющих эти точки (ребер). Обозначать граф будем буквой Г. Вершины графа будем обозначать прописными буквами русского (латинского) алфавита или числами (например, А, Б, В,…,A, B, C, D,…,1, 2,…); ребра – парами вершин, принадлежащих данным ребрам или строчными буквами русского (латинского) алфавита (например, (А,Б), (N,F), (3,4), а, б, в, k, l, m). Иногда будем изображать граф, не обозначая его ребра и вершины.
Пример. Граф с вершинами A, B, C, D, E, ребрами (A, B), (B, D), (C, E), (E, D). 20 – вес ребра (А, В), 15 – вес ребра (С, Е) и т.д. Вершины графа обычно изображают “жирными” точками, кружками или квадратиками, так как ребра графа иногда пересекаются на чертеже, но точка пересечения при этом не является вершиной. Пример.
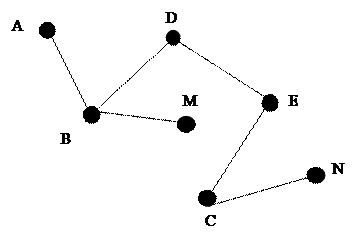
В данном графе точка пересечения диагоналей четырехугольника не является вершиной графа.
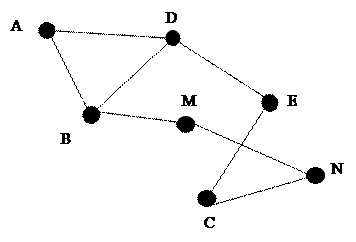
А в этом графе точка пересечения диагоналей четырехугольника является вершиной графа. Не всегда все вершины графа соединены друг с другом. Иногда вершина не соединена ни с одной из вершин графа.
Вершина 5 является изолированной.
Решение. Все вершины графа являются изолированными, то есть ни одна пара вершин не соединена ребром. Таким образом, все пять жителей не знакомы друг с другом. Определение. Вершина А графа Г, принадлежащая одному ребру, называется висячей. Пример. Вершины А и Б - висячие.
Пример. Укажите висячие вершины. Объясните ответ. Есть ли здесь изолированные вершины? Объясните ответ.
Ответ: 1, 4, 5 – висячие вершины по определению. Изолированных вершин нет по определению. Определение. Степенью вершины А графа Г называется количество ребер графа Г, которым данная вершина принадлежит. Обозначают степень вершины А: deg (A). В случае изолированной вершины deg (A) = 0; для висячей вершины deg (A) = 1. Пример. В следующих графах найдите степени каждой из вершин.
а) б) Решение. а) deg (1) = deg (2) = deg (3) = deg (4) = deg (5) = 2; б) deg (1) = deg (2) = deg (4) = 1 – это висячие вершины, deg (5) = 0 – это изолированная вершина, deg (3) = 2, deg (6) = 3. Установим связь между степенями вершин графа и числом его ребер. Пример. Найдите количество ребер Р графа Г и сумму степеней С всех его вершин.
Ответ: Р = 4, С=1+2+3+2=8. Заметим, что сумма всех степеней вершин графа в два раза больше, чем число его ребер. Теорема. Сумма степеней вершин графа Г равна удвоенному числу ребер, то есть Определение. Пусть дан граф Г с вершинами Из определения следует, что каждые два соседних ребра пути имеют общую вершину и никакое ребро не встречается более одного раза. Пример. (M, B), (B, D), (D, E), (E, C), (C, N) – путь в данном графе из вершины М в вершину N.
Пример. Являются ли путями из вершины 1 в вершину 5 следующие последовательности ребер: а) (1,2),(3,4),(4,5) – нет, т.к. ребра (1,2) и (3,4) – соседние, но не имеют общей вершины; б) (1,2),(2,3),(3,4) – нет, т.к. эта последовательность не ведет в вершину 5; в) (1,2),(2,4),(4,3),(3,2),(2,4),(4,5) – нет, т.к. ребро (2,4) повторяется. Найдите путь от вершины 1 к вершине 5 в графе, изображенном на рисунке.
Ответ: (1,2),(2,3),(3,4),(4,5) или (1,2),(2,4),(4,5). Сравним два полученных в задаче пути. Очевидно, второй из них короче. Значит можно говорить о длине пути в графе. Определение. Длиной пути в графе Г называется количество входящих в этот путь ребер. Пример. (M, B), (B, D), (D, E), (E, C), (C, N) – путь в данном графе из вершины М в вершину N. Длина пути равна пяти.
Определение. Циклом графа Г называется такой путь в этом графе, у которого начало совпадает с концом.
(M, B), (B, D), (D, E), (E, C), (C, N), (N, M) – цикл в данном графе. (A, B), (B, D), (D, A) – цикл в данном графе. Определение. Длиной цикла называется количество входящих в него ребер. Пример. Для данного графа назвать все содержащиеся в нем циклы и выбрать наибольший и наименьший по длине цикл.
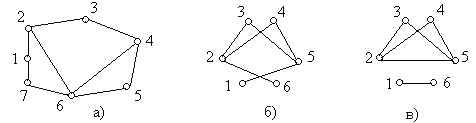
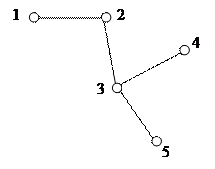
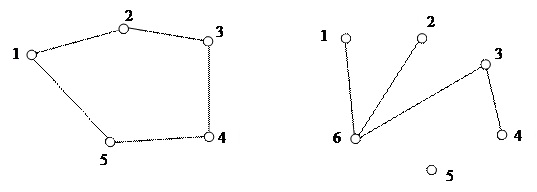
Решение. а) (1,2),(2,3),(3,4),(4,5),(5,6),(6,7),(7,1) – самый длинный цикл; (1,2),(2,6),(6,7),(7,1); (2,3),(3,4),(4,6),(6,2); (1,2),(2,3),(3,4),(4,6),(6,7),(7,1); (2,3),(3,4),(4,5),(5,6),(6,2); (4,5),(5,6),(6,4) – самый короткий цикл; Определение. Граф называется связным, если между любыми двумя его вершинами существует путь. В противном случае граф называется несвязным. Определение. Две вершины А и В графа называются связными, если в графе существует путь с концами А и В; если не существует ни одного пути, связывающего их, то вершины называются несвязными. Из определения следует, что граф является связным, если каждые две его вершины связны, и граф является несвязным, если хотя бы две его вершины несвязны. Таким образом, чтобы доказать, что граф связный, нужно доказать, что каждые две его вершины являются связными. А чтобы доказать, что граф несвязный – нужно указать в нем две несвязные вершины. Пример. Какие из графов являются связными? Почему?
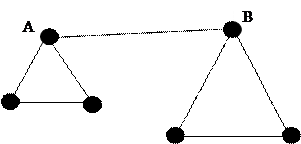
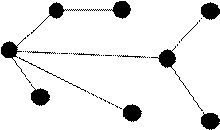
Ответ: связными являются графы г) и д). Определение. Ребро (А, В) называется мостом графа Г, если в графе, полученном после удаления из Г ребра (А, В), вершины А и В оказываются несвязными. Пример.
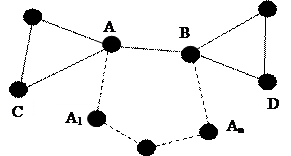
Теорема. Ребро (А, В) является мостом в том и только том случае, если (А, В) – единственный путь, соединяющий вершины А и В.
Теорема. Ребро (А, В) является мостом в том и только том случае, если найдутся две вершины С, D такие, что каждый путь, соединяющий их, содержит вершины А и В.
Теорема. Ребро (А, В) является мостом в том и только том случае, если оно не принадлежит ни одному циклу.
Вопросы для самопроверки
Задания для самостоятельного решения Задание № 1. Укажите множество действительных чисел, соответствующее записи.
Задание № 2. Дано множество Mi:
Приведите по три примера элементов множества Mi. Укажите, каким из множеств, принадлежат числа 3, 4, 5, 13, 25, Задание № 3. Задать различными способами множество M всех чисел, являющихся степенями двойки: 2, 4, 8, 16, …, не превышающих 300. Задание № 4. Задать различными способами множество натуральных чисел, кратных пяти: 5, 10, 15, 20, …. Задание № 5. Пусть универсальное множество I – множество всех студентов некоторого техникума; А – множество всех студентов техникума в возрасте старше 18 лет; В – множество студентов, учащихся на «4» и «5»; С – множество студентов, посещающих спортивные секции. Каков содержательный смысл (характеристическое свойство) каждого из следующих множеств?
Задание № 6. Осуществить операции над множествами Задание № 7. Пусть
Задание № 8. Даны отрезки А = [-4; 5], B = (2; 6], C = (5; 10]. Найдите следующие множества и изобразите их кругами Эйлера:
Задание № 9. В штучном отделе магазина покупатели обычно покупают либо один торт, либо одну коробку конфет, либо один торт и одну коробку конфет. В один из дней было продано 57 тортов и 36 коробок конфет. Сколько было покупателей, если 12 человек купили и торт, и коробку конфет? Задание № 10. Начертите граф, содержащий: а) четыре висячих и две изолированные вершины. б) шесть висячих и две изолированные вершины. Задание № 11. Найдите количество ребер Р графа Г и сумму степеней С всех его вершин.
Задание № 13. Является ли циклом следующая последовательность ребер:
а) (A,B),(B,E),(E,D),(D,B),(B,A); б) (D,E),(E,B),(B,D),(D,C); в) (D,C),(C,B),(B,E),(E,D); г) (B,E),(D,C),(C,B)? Задание № 14. Для каждого из изображенных на рисунке графов назвать все содержащиеся в них циклы и выбрать наибольший и наименьший по длине цикл.
VI. Ряды Числовые ряды
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 559; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.205.154 (0.185 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 ).
).

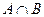 ).
).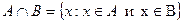

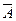 )
)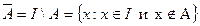

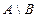 ).
).
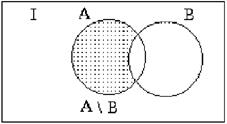
 (обозначается
(обозначается 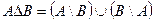 ).
).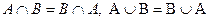 - переместительный закон для операций объединения и пересечения.
- переместительный закон для операций объединения и пересечения.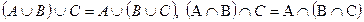 - сочетательный закон для операций объединения и пересечения.
- сочетательный закон для операций объединения и пересечения.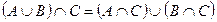 - распределительный закон пересечения относительно объединения множеств.
- распределительный закон пересечения относительно объединения множеств.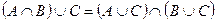 - распределительный закон объединения относительно пересечения множеств.
- распределительный закон объединения относительно пересечения множеств.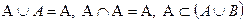 - законы поглощения.
- законы поглощения.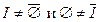 - универсальное и пустое множества являются дополнениями друг друга.
- универсальное и пустое множества являются дополнениями друг друга.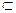 I справедливо
I справедливо 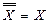 .
. или
или 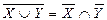 .
.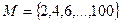 .
.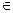 M;
M;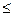 98.
98.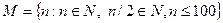
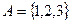 ; в)
; в) 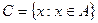
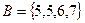 г)
г) 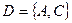 ?
?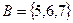 .
.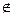 D, так как элемент 1 не перечислен в списке.
D, так как элемент 1 не перечислен в списке.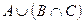 д)
д)  ?
? г)
г) 
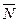 , если М – множество всех натуральных чисел, не превосходящих 100; N – множество натуральных чисел.
, если М – множество всех натуральных чисел, не превосходящих 100; N – множество натуральных чисел.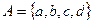 и
и 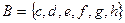
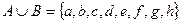
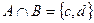


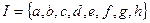 , тогда
, тогда  ,
,  .
.
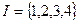 ,
, 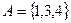 ,
, 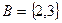 ,
, 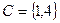
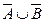 ; б)
; б) 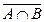 ; в)
; в) 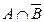 ; г)
; г) 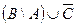


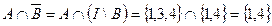
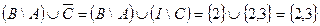
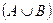 = 250. Студенты, получившие оценки «3» и «4», образуют множество
= 250. Студенты, получившие оценки «3» и «4», образуют множество 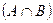 .
.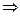
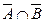 . По условию
. По условию  . Отсюда
. Отсюда  - умеют кататься на чем-нибудь.
- умеют кататься на чем-нибудь.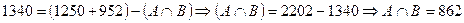 .
.

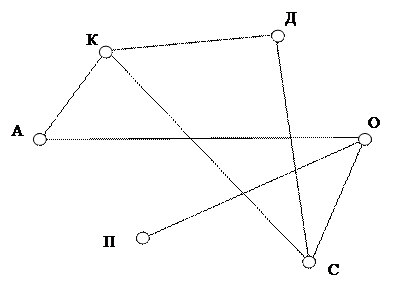 Представим данные задачи на чертеже. Обозначим участников соревнования точками так, что Кириллу будет соответствовать точка К, Денису – точка Д и т.д. Если двое участников уже сыграли между собой, то соединим изображающие их точки отрезками.
Представим данные задачи на чертеже. Обозначим участников соревнования точками так, что Кириллу будет соответствовать точка К, Денису – точка Д и т.д. Если двое участников уже сыграли между собой, то соединим изображающие их точки отрезками.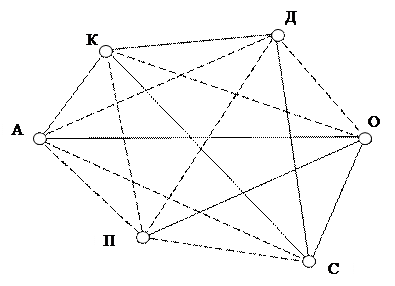
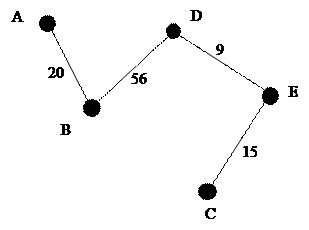 В некоторых случаях каждому ребру графа присваивают некоторое число. Это число называется весом данного ребра.
В некоторых случаях каждому ребру графа присваивают некоторое число. Это число называется весом данного ребра.

 Определение. Вершина графа, не принадлежащая ни одному ребру, называется изолированной.
Определение. Вершина графа, не принадлежащая ни одному ребру, называется изолированной.
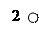

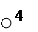




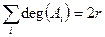 , где r – число ребер.
, где r – число ребер.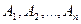 . Путем в графе Г называется последовательность ребер
. Путем в графе Г называется последовательность ребер 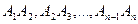 . Причем вершина
. Причем вершина 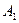 называется началом пути, а вершина
называется началом пути, а вершина  – концом пути.
– концом пути. M – начало пути; N – конец пути.
M – начало пути; N – конец пути.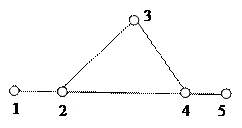
 Пример.
Пример.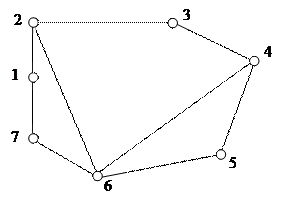


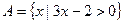
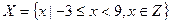


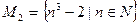

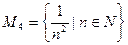

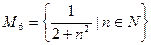
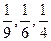 . Укажите, каким из множеств не принадлежат указанные числа. Запишите эти утверждения символически.
. Укажите, каким из множеств не принадлежат указанные числа. Запишите эти утверждения символически.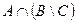
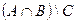
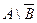


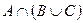
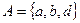 и
и 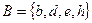 , если
, если 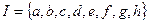 .
.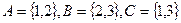 . Найти:
. Найти:
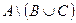
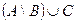


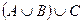
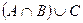
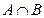
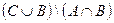


 а) б) г)
а) б) г) Задание № 12. Укажите все пути, соединяющие вершины 1 и 4 в графе, изображенном на рисунке. Сколько существует путей длины два в этом графе?
Задание № 12. Укажите все пути, соединяющие вершины 1 и 4 в графе, изображенном на рисунке. Сколько существует путей длины два в этом графе?