
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные сведения из теории степенных рядов.
Пусть задана бесконечная последовательность функций
имеющих общую область определения. Определение. Функциональным рядом называется составленное из этих функций выражение Если в членах ряда
Если при Пример. Функциональный ряд
cходится в точке x = ½ и расходится в точке x = 2. В самом деле, подставляя в условие x = ½, получим числовой ряд Данный функциональный ряд расходится в точке x = 2, так как числовой ряд Определение. Областью сходимости функционального ряда называется множество всех точек сходимости этого ряда. Если значение
Таким образом, значение суммы функционального ряда зависит от значения
где Частным случаем функционального ряда является степенной ряд. Определение. Степенным рядом называется функциональный ряд вида Числа Пример. Следующие функциональные ряды а) б) являются степенными рядами. При
Исследование вопроса о сходимости степенного ряда 1. Степенной ряд расходится для всех значений x, кроме x=0 (при x=0 степенной ряд сходится и его сумма равна 2. Степенной ряд сходится при любом значении x. Тогда его называют всюду сходящимся. 3. Степенной ряд сходится при одних значениях x и расходится при других значениях x. Теорема Абеля позволяет определить форму области сходимости степенного ряда. Теорема Абеля. Если ряд Если ряд
Замечание. Из теоремы следует, что если при Определение. Интервалом сходимости степенного ряда называется промежуток (- R, R) такой, что для всякой точки x, которая лежит внутри этого интервала, ряд сходится (абсолютно), а для точек x, лежащих вне его, ряд расходится. Число R называется радиусом сходимости. Радиус сходимости ряда Если где
Ряд будет абсолютно сходится при значениях х, удовлетворяющих неравенству Если
Это значит, что степенной ряд сходится при любом значении х (сходится всюду). Если
т.е. интервал сходимости вырождается в точку (ряд Исследовать степенной ряд на сходимость означает найти его интервал сходимости и установить сходимость или расходимость ряда в граничных точках интервала, т.е. при Чтобы найти область сходимости степенного ряда
необходимо: 1) Найти коэффициенты 2) Составить отношение 3) Найти Пусть этот предел равен L, тогда радиус сходимости степенного ряда 4) Исследовать поведение степенного ряда в граничных точках интервала сходимости Пример. Найти область сходимости ряда
1) Коэффициент n – го члена 2) Их отношение 3) Вычислим Радиус сходимости 4) Исследуем сходимость ряда в граничных точках интервала сходимости. Подставляем в заданный ряд
который абсолютно сходится по признаку сходимости знакочередующегося ряда. На правом конце интервала сходимости
который расходится по теореме (предельная форма признака сравнения). Таким образом, область сходимости степенного ряда [-3,1). Пример. Найти область сходимости ряда
К этому ряду формула
Применим признак Даламбера. Так как
|
||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 67; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.100.34 (0.015 с.) |
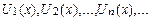 ,
,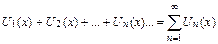 .
. 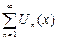 зафиксировать значение аргумента
зафиксировать значение аргумента 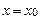 , то получим числовой ряд
, то получим числовой ряд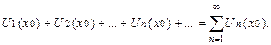
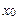 называется точкой сходимости функционального ряда.
называется точкой сходимости функционального ряда.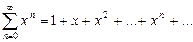
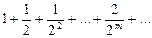 , который сходится.
, который сходится.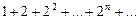 является расходящимся.
является расходящимся.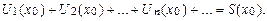
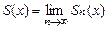 - сумма ряда,
- сумма ряда,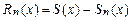 - остаток ряда,
- остаток ряда,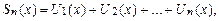 а x принадлежит области сходимости.
а x принадлежит области сходимости.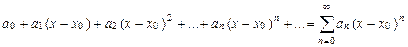
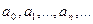 называются коэффициентами степенного ряда (некоторые из них могут быть равны нулю), х - независимая переменная, х 0 – фиксированное число.
называются коэффициентами степенного ряда (некоторые из них могут быть равны нулю), х - независимая переменная, х 0 – фиксированное число.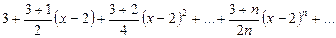
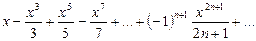
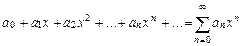 .
. 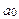 . Это тривиальный случай.)
. Это тривиальный случай.)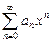 сходится при некотором значении
сходится при некотором значении 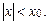
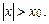
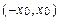 ряд сходится абсолютно. Если при
ряд сходится абсолютно. Если при 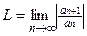 ,
,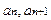 - коэффициенты соответственно n – го и (n+1) – го членов ряда, то радиус сходимости степенного ряда
- коэффициенты соответственно n – го и (n+1) – го членов ряда, то радиус сходимости степенного ряда 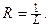
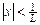 , т.е. для всех значений из интервала
, т.е. для всех значений из интервала 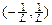 .
.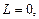 то
то 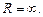
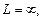 то
то 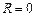
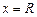 и
и 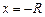 .
.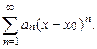
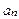 и
и 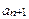 n – го и (n+1) – го членов ряда.
n – го и (n+1) – го членов ряда.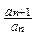 и взять его по абсолютной величине.
и взять его по абсолютной величине.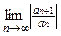 .
.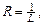 а его интервалом сходимости будет интервал
а его интервалом сходимости будет интервал 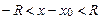 .
.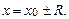
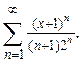
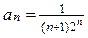 ; коэффициент (n+1) – го члена
; коэффициент (n+1) – го члена 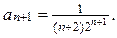
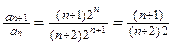 .
.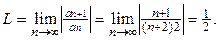
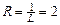 . Следовательно, интервал сходимости определяется неравенствами
. Следовательно, интервал сходимости определяется неравенствами 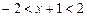 . Таким образом, ряд абсолютно сходится для всех значений х из интервала (-3,1).
. Таким образом, ряд абсолютно сходится для всех значений х из интервала (-3,1).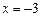 . Получим числовой ряд
. Получим числовой ряд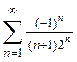 ,
,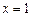 ; подставляя это значение в заданный ряд, получим
; подставляя это значение в заданный ряд, получим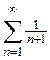 ,
,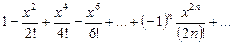
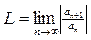 не применима, так как отсутствуют нечетные степени переменной x, т.е.
не применима, так как отсутствуют нечетные степени переменной x, т.е. 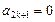 , k = 0,1,2, …. Применяем непосредственно признак Даламбера:
, k = 0,1,2, …. Применяем непосредственно признак Даламбера: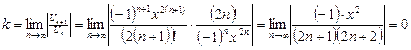
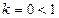 , то ряд сходится на всей числовой прямой.
, то ряд сходится на всей числовой прямой.


