Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы приближенного дифференцирования, основанные на первой итерационной формуле Ньютона.
Пусть имеем функцию y(x), заданную в равноотстоящих точках Имеем:
Где:
Здесь: Разности высших порядков будут:
Производя перемножение биномов, получим:
Так как
То
Аналогично, так как:
То
Таким же способом в случае надобности можно вычислить и производные функции y (x) любого порядка. Заметим, что при нахождении производных Иногда требуется находить производные функции у в основных табличных точках xi. В этом случае формулы численного дифференцирования упрощаются. Так как каждое табличное значение можно считать за начальное, то положим x= x0, q= 0; тогда будем иметь:
и Пример. 1) Найти Значения функции
Здесь h=5. (десятичные разряды, как обычно, не указываются; они определяются десятичными разрядами значений функции). Используя первую строчку таблицы, на основании формулы
2) Вычислить приближенное значение производной функции
Используя таблицу, в соответствии с формулой рассчитаем приближенное значение производной функции y = ex в точке x = 1,05. Полагая x0 = 1,0, шаг h = 0,1, x = 1,05 вычислим:
Вычислим абсолютную и относительную погрешность результата. Учитывая, что Δ = Относительная погрешность: ω = Численное интегрирование Постановка задачи Из курса математического анализа известно, что, если функция f(x) непрерывна на отрезке [a;b] и дифференцируема, то определенный интеграл от этой функции в пределах от a до b существует и может быть вычислен по формуле Ньютона-Лейбница:
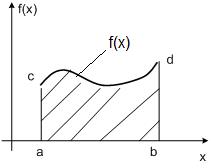
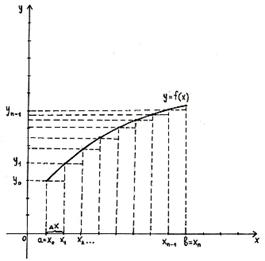
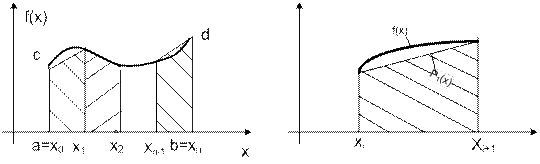
Если первообразную функцию F(x) не удается выразить аналитически через элементарные функции или если при проведении практических расчетов подынтегральная функция f(x) задается в виде таблицы, то это приводит к необходимости замены аналитического интегрирования численными методами. Для функции f(x), заданной в прямоугольной системе координат на интервале [a;b], этот интеграл численно равен площади, ограниченной кривой f(x), осью Ox и двумя ординатами ac и bd.
Задача численного интегрирования заключается в нахождении значения определенного интеграла через ряд значений подынтегральной функции yi=f(xi), заданной в точках xi (i=0,1,…,n). Причем, x0 = a, xn = b. Чаще всего интервал разбивают на подынтервалы длинойh = xi+1 - xi. Для получения простых формул интегрирования используют полиномы нулевой, первой и второй степени и соответственно получают формулы численного интегрирования: прямоугольников, трапеций и Симпсона. 2) Простейшим приближённым методом является метод прямоугольников. Геометрически идея способа вычисления определённого интеграла по формуле прямоугольников состоит в том, что площадь криволинейной трапеции заменяется суммой площадей прямоугольников, одна сторона которых равна Если суммировать площади прямоугольников, которые показывают площадь криволинейной трапеции с недостатком, то получим формулу:
Если с избытком, то Значения у0, у1,..., уn находят из равенств Итак, чтобы найти приближённое значение интеграла · разделить отрезок интегрирования [ a, b ] на n равных частей точками х0= а, х1, х2,..., х n -1, х n = b; · вычислить значения подынтегральной функции · воспользоваться одной из приближённых формул. Для того, чтобы найти погрешность вычислений, надо воспользоваться формулами:
Пример. Вычислить по формуле прямоугольников Решение: Разобьём отрезок [ a, b ] на несколько (например, на 6) равных частей. Тогда а = 0, b = 3, х k = a + k f (x 0) = 22 = 4
По формуле
Для того, чтобы вычислить относительную погрешность вычислений, надо найти точное значение интеграла:
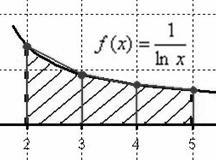
Формула трапеций Разобьем интервал интегрирования [a;b] на n равных отрезков и восстановим из полученных точек a, х1, x2, …, b перпендикуляры до пересечения с графиком функции. Соединив последовательно точки пересечения, представим площадь полученной криволинейной трапеции как сумму прямолинейных трапеций, площади которых легко подсчитать. Заменив подынтегральную функцию f(x) в пределах элементарного отрезка [xi;xi+1] интерполяционным многочленом первой степени, получим следующие формулы для элементарных площадей:
Тогда общая площадь равна: Отсюда получаем формулу трапеций:
Пример. Вычислить приближенно определенный интеграл по формуле трапеций. Результаты округлить до трёх знаков после запятой.
а) Точек xi будет на одну больше, чем количество отрезков: х i = a + i
В соответствии с условием задачи, все вычисления следует округлять до 3-его знака после запятой. Окончательно:
б) Разобьём отрезок интегрирования на 5 равных частей, то есть n = 5. Если n = 5, то формула трапеций принимает следующий вид:
При чистовом оформлении задачи все вычисления удобно оформлять расчетной таблицей:
a = x0 = 2 остальные значения получаем по формуле х i= a + i х 1 = 2 + 0,6 х 4 = 2 + 0,6
Формула Симпсона Это более совершенный способ – график подынтегральной функции приближается не ломаной линией, а маленькими параболами. Сколько промежуточных отрезков – столько и маленьких парабол. Если взять те же три отрезка, то метод Симпсона даст ещё более точное приближение, чем метод прямоугольников или метод трапеций. Рассмотрим определенный интеграл На практике отрезков может быть:
Итак, наше разбиение имеет следующий вид:
Формула Симпсона для приближенного вычисления определенного интеграла имеет следующий вид:
Пример. Вычислить приближенно определенный интеграл по формуле Симпсона с точностью до 0,001. Разбиение начать с двух отрезков 2 n = 2.
Если у нас два отрезка разбиения 2 n = 2, то узлов будет на один больше:
Заполним расчетную таблицу:
В результате:
Заполним расчетную таблицу:
Таким образом:
больше требуемой точности: то необходимо еще раз удвоить количество отрезков: 2 n = 8. Формула Симпсона примет вид:
И снова заполним расчетную таблицу:
Таким образом:
Оцениваем погрешность:
Итак, Пример. Вычислить значение определенного интеграла Предположим, что, подынтегральная функция задана таблично:
Используем формулы прямоугольников:
считая, что
Используем формулу трапеций:
Формула Симпсона примет вид:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.126.80 (0.067 с.) |
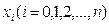 отрезка [a,b] с помощью значений
отрезка [a,b] с помощью значений 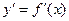 ,
, 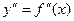 и т.д. Функцию y приближенно заменим интерполяционным полиномом Ньютона, построенным для системы узлов x0, x1,…,
и т.д. Функцию y приближенно заменим интерполяционным полиномом Ньютона, построенным для системы узлов x0, x1,…, 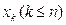 .
.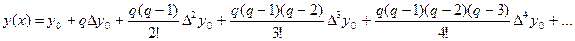
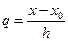 и
и 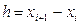 (i=0,1,…)
(i=0,1,…)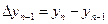 , откуда
, откуда 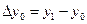 ;
; 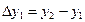 ;
;  ; …..
; …..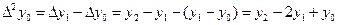
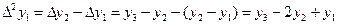
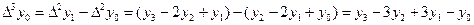
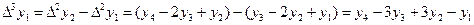
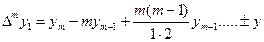

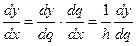
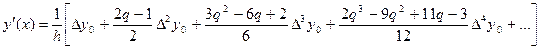
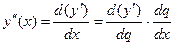

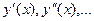 в фиксированной точке x в качестве x0 следует выбирать ближайшее табличное значение аргумента.
в фиксированной точке x в качестве x0 следует выбирать ближайшее табличное значение аргумента.
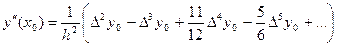
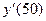
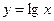
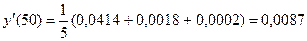
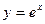 в точке x = 1,05 на интервале [1; 1,3] при разбиении интевала на 3 равные части с использованием формулы, основанной на первой интерполяционной формуле Ньютона. Найти абсолютную и относительную погрешность результата.
в точке x = 1,05 на интервале [1; 1,3] при разбиении интевала на 3 равные части с использованием формулы, основанной на первой интерполяционной формуле Ньютона. Найти абсолютную и относительную погрешность результата.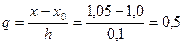
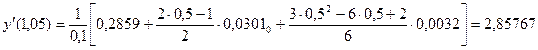
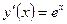 , то
, то 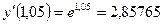 , то абсолютная погрешность результата равна:
, то абсолютная погрешность результата равна: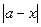 =
= 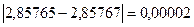
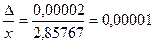

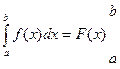
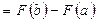
 Метод прямоугольников
Метод прямоугольников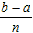 , а другая -
, а другая - 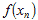 .
.
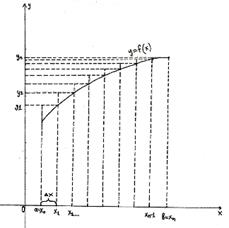
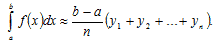
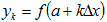 , к = 0, 1..., n. Эти формулы называются формулами прямоугольников и дают приближённый результат. С увеличением n результат становится более точным.
, к = 0, 1..., n. Эти формулы называются формулами прямоугольников и дают приближённый результат. С увеличением n результат становится более точным.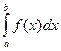 , нужно:
, нужно: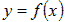 в точках деления, т.е. найти у 0 = f (x0), у 1 = f (x1), у 2 = f (x2), у n -1 = f (xn-1), у n = f (xn);
в точках деления, т.е. найти у 0 = f (x0), у 1 = f (x1), у 2 = f (x2), у n -1 = f (xn-1), у n = f (xn);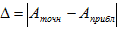
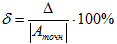
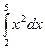 . Найти абсолютную и относительную погрешности вычислений.
. Найти абсолютную и относительную погрешности вычислений.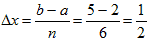

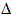 х
х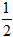 = 2
= 2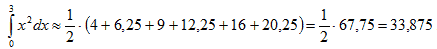
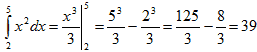
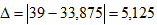
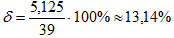
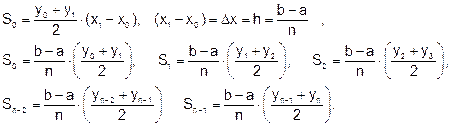
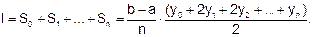
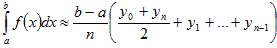
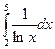
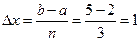 .
.
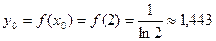
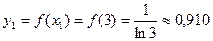
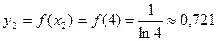
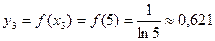
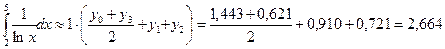
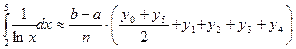
 , то есть, длина каждого промежуточного отрезка равна 0,6.
, то есть, длина каждого промежуточного отрезка равна 0,6.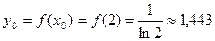
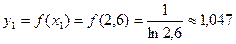
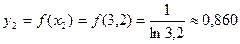
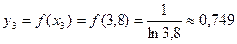
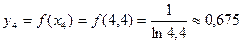
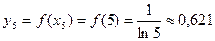
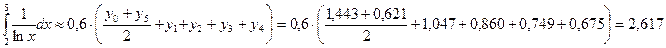
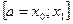 ,
, 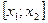 ,
, 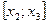 , …
, … 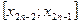 ,
, 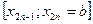
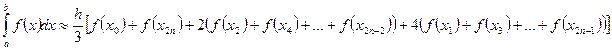 , где:
, где: 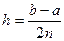 – длина каждого из маленьких отрезков или шаг;
– длина каждого из маленьких отрезков или шаг;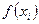 – значения подынтегральной функции в точках
– значения подынтегральной функции в точках 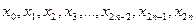 .
.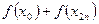 – сумма первого и последнего значения подынтегральной функции;
– сумма первого и последнего значения подынтегральной функции;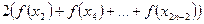 – сумма членов с чётными индексами умножается на 2;
– сумма членов с чётными индексами умножается на 2;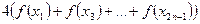 – сумма членов с нечётными индексами умножается на 4.
– сумма членов с нечётными индексами умножается на 4.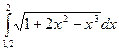
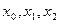 . И формула Симпсона принимает весьма компактный вид:
. И формула Симпсона принимает весьма компактный вид: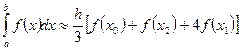
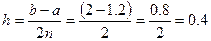
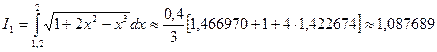
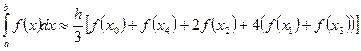
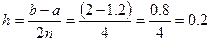
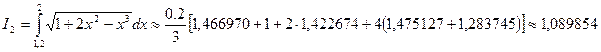
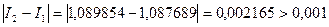
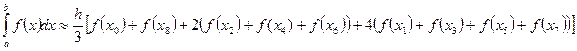
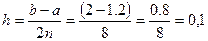
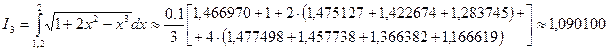
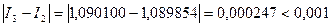
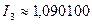 , округлить его до трёх знаков после запятой и записать:
, округлить его до трёх знаков после запятой и записать: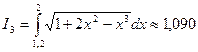 с точностью до 0,001
с точностью до 0,001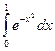
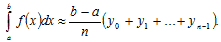
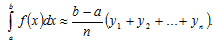
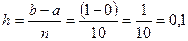 имеем:
имеем: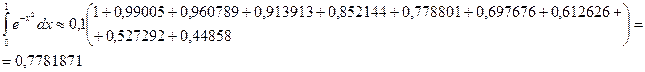
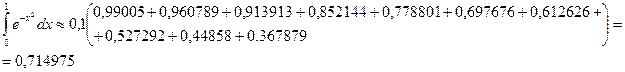
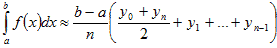
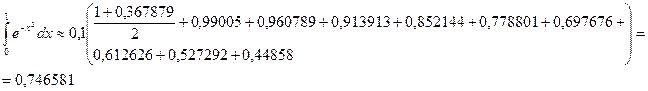 Используем формулу Симпсона при2n = 10:
Используем формулу Симпсона при2n = 10: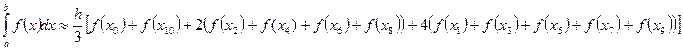 Вычислим шаг:
Вычислим шаг: