
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные методы интегрированияСтр 1 из 9Следующая ⇒
Основные понятия неопределенного интеграла Неопределенным интегралом функции f (x) называется множество всех первообразных функций F (x) + C. Записывается это так: Первообразной функцией для функции f (x) на промежутке (a; b) называется такая функция F (x), производная которой равна f (x) на рассматриваемом промежутке, то есть Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции. Имеет место теорема: Две различные первообразные одной и той же функции, определенной в некотором промежутке, отличаются друг от друга в этом промежутке на некоторое постоянное слагаемое. Функция f (x) называется непрерывной на отрезке [ a, b ], если 1) она определена на этом множестве; 2) непрерывна в каждой точке этого отрезка, то есть Теорема (условие существования неопределенного интеграла). Всякая непрерывная на отрезке [ a, b ] функция имеет на этом промежутке неопределенный интеграл. Основные теоремы (свойства неопределенного интеграла): 1. 2. 3. 4. 5. 6. (Инвариантность формулы интегрирования). Если Ниже приводится таблица основных интегралов, которые используются при вычислениях неопределенных интегралов различных функций. Верность этой таблицы проверяется непосредственно дифференцированием. Таблица 1.
Основные методы интегрирования Метод непосредственного интегрирования Метод интегрирования основан на применении табличных интегралов, и называется непосредственным интегрированием. При этом данный интеграл может быть приведен к табличному с помощью тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла. Примеры: a) b)
с) Замена переменной Этот метод интегрирования основан на введении новой переменной интегрирования. Приведем пример: пусть дана сложная функция f (x), где
Эта формула называется формулой замены переменной в неопределенном интеграле. Примеры: a)
b)
с) Первый вариант замены: Второй вариант замены:
d)
Второй вариант замены: = При интегрировании заменой переменной важно удачно сделать подстановку. Однако нельзя дать общее правило выбора замены переменной для интегрирования любой функции. Это можно сделать только для интегрирования отдельных классов функций: рациональных, тригонометрических и т.д. (интегрирование этих классов функций предложены в таблицах 3 – 7). Интегрирование по частям Этот метод интегрирования основан на применении формулы дифференцирования произведения d (uv)= udv + vdu и вычислении затем интеграла Примеры: a) Интегирируется по частям: пусть Еще раз интегрируется по частям: пусть
b) Интегирируется по частям: пусть
c) Интегирируется по частям: пусть Получившийся интеграл вычисляется методом замены переменной:
d) Пусть Интегирируется по частям: пусть
e) Интегирируется по частям: пусть
Обозначается, Следовательно, f) Интегирируется по частям: пусть
g) Интегрируется по частям: пусть Еще раз интегрируется по частям: пусть
= Обозначается, Следовательно, h) Интегрируется по частям: пусть
Еще раз интегрируется по частям: пусть
Обозначают, Следовательно, k) Интегрируется по частям: пусть тогда Следовательно,
Приведем в таблице 2 некоторые распространённые случаи использования метода интегрирования по частям.
Таблица 2.
Примеры интегралов, не выражающихся через Элементарные функции 1. Интеграл вида a) Р(х) – многочлен третей или четвёртой степени без кратных корней, такой многочлен называется эллиптическим: · · · (0 < k < 1, h – комплексное число) b) Р(х) – многочлен степени выше четвертой, то интеграл называется ультраэллиптическим. c) Р(х) – многочлен выражаемый через элементарные функции называется псевдоэллиптическим. 2. 3. 4. 5. 6. Задания для самопроверки №1 Вычислить: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. Используя метод интегрирования по частям, доказать, что: а) b) c)
§2. Определенный интеграл Основные понятия и методы решения определенного интеграла Пусть на отрезке [a, b] задана непрерывная функция f (x) [см. § 1]. Разобьём отрезок [a, b] произвольным образом на п частей точками Определённым интегралом от функции f (x) на отрезке [a, b] называется число равное пределу интегральных сумм при стремлении к нулю
Определённый интеграл обозначается символом
Пусть на отрезке [ a, b ] задана непрерывная функция Геометрический смысл определённого интеграла: определённый интеграл равен площади «криволинейной трапеции» ограниченной функцией Теорема. Если функция f (x) непрерывна на отрезке [ a, b ], то определённый интеграл Отметим, что если оставить постоянным нижний предел интегрирования а, а верхний х изменить так, что бы Теорема ( Связь между неопределённым интегралом и определённым интегралами). Всякая непрерывная на отрезке [ a, b ] функция Теорема (Ньютона – Лейбница). Если функция F(x) – какая- либо первообразная от непрерывной функции f (x), то Основные свойства определенного интеграла: 1. 2. 3. 4. Если f (x) £ j (x) на отрезке [ a, b ] a < b, то 5. Если m и M – соответственно наименьшее и наибольшее значения функции f (x) на отрезке [ a, b ], то: 6. Теорема о среднем. Если функция f (x) непрерывна на отрезке [a, b], то на этом отрезке существует точка e такая, что 7. Для произвольных чисел a, b, c справедливо равенство: 8. 9. Формула прямоугольников
Разобьем отрезок [ a, b ] на n равных частей, длины которых равны При таком разбиении имеем прямоугольники, площадь которых равна Тогда сумма площадей всех прямоугольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение определенного интеграла и называемое общей формулой прямоугольников:
Формула трапеций
Подынтегральная функция в этом случае заменяется на вписанную ломаную. Геометрически площадь криволинейной трапеции заменяется суммой площадей вписанных трапеций.
Замечание: чем больше взять точек n разбиения интервала, тем с большей точностью будет вычислен интеграл. Площади вписанных трапеций вычисляются по формулам:
После приведения подобных слагаемых получаем формулу трапеций:
Формула парабол (формула Симпсона или квадратурная формула)
Площадь криволинейной трапеции, ограниченной графиком функции f (x) заменим на площадь криволинейной трапеции, ограниченной параболой второй степени с осью симметрии, параллельной оси OY и проходящей через точки кривой, со значениями f (x 0), f (x 1), f (x 2). Для каждой пары отрезков построим такую параболу.

      Уравнения этих парабол имеют вид Уравнения этих парабол имеют вид
Ax2 + Bx + C, где коэффициенты А, В, С могут быть легко найдены по трем точкам пересечения параболы с исходной кривой. Для определения А, В, С имеется система уравнений:
Выразается S через величины (1): C учетом этого: Отсюда выражение (2) примет вид: Тогда для каждой пары отрезков имеется:
Суммируя эти выражения, получаем формулу называемую формулой Симпсона: Пример: Вычислим приближенное значение определенного интеграла
Точное значение этого интеграла: 91.173. Для сравнения применим к этой же задаче формулу трапеций.
Несобственные интегралы 1.Несобственные интегралы первого рода Если функция
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; если предел не существует или бесконечен, то несобственный интеграл называется расходящимся. Теоремы о сходимости и расходимости: 1. Если на промежутке 2. Если при 3. Если сходится интеграл Примеры: 1.
2. 2.Несобственные интегралы второго рода (интеграл от разрывной функции) Если функция Если функция Замечание: внутренних точек разрыва II-го рода внутри отрезка может быть несколько. Теоремы о сходимости и расходимости: 1. Если на промежутке 2. Пусть функции 3. Если функция Задания для самопроверки №2 Вычислить: 1. 2. 3. 4. 5. 6. 7. 8. Исследовать на сходимость несобственные интегралы: a) b) c) d) Интеграла 1. Вычисление объём тела по известным площадям параллельных сечений
Тогда объем этого тела вычисляется по формуле 2. Объёмы тел вращения Пусть кривая, задана уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [ a, b ]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения.
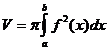 , где V – объем тела, полученного вращением криволинейной трапеции 0 £ y £ f(x), , где V – объем тела, полученного вращением криволинейной трапеции 0 £ y £ f(x),
a £ x £ b вокруг оси Ох.
 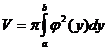 , где V – объем тела, полученного вращением криволинейной трапеции 0 £ x £ j (y), , где V – объем тела, полученного вращением криволинейной трапеции 0 £ x £ j (y),
c £ y £ d вокруг оси ОУ.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 474; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.114.142 (0.158 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
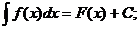
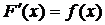 .
.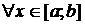 справедливо равенство
справедливо равенство 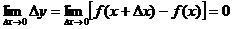 , где
, где  .
.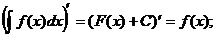 где C-const.
где C-const.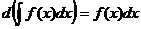 .
.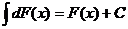 .
.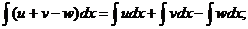 где u, v, w – некоторые функции от х.
где u, v, w – некоторые функции от х.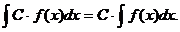
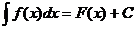 , то и
, то и  , где
, где 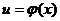 - произвольная функция, имеющая непрерывную производную.
- произвольная функция, имеющая непрерывную производную.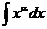

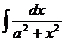

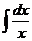
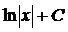
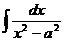



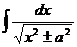
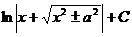
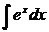
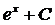
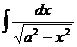
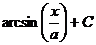
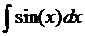


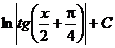

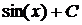
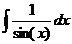
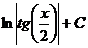

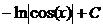
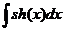
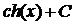
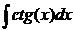
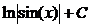
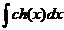


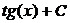
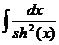

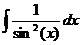

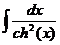


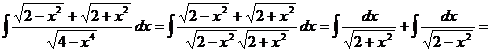
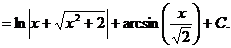
 .
.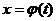 - функция имеющая непрерывную производную
- функция имеющая непрерывную производную  . Применяется свойство инвариантности формулы интегрирования неопределенного интеграла, получаем:
. Применяется свойство инвариантности формулы интегрирования неопределенного интеграла, получаем:  .
.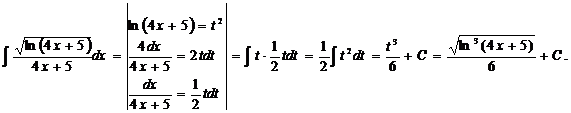
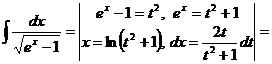

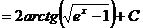 .
.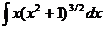 .
.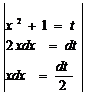 =
= 
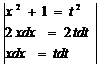 =
= 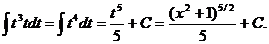
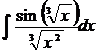 . Первый вариант замены:
. Первый вариант замены: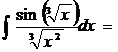
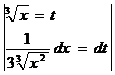 =
= 
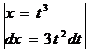 =
= 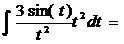
 . Из этого равества получаем формулу интегрирования по частям:
. Из этого равества получаем формулу интегрирования по частям:  .
.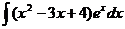
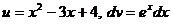 ; тогда
; тогда 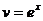 ,
, 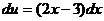 . Следовательно,
. Следовательно, 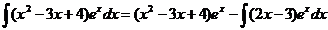 .
.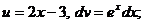 тогда
тогда 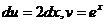 . Получаем,
. Получаем, 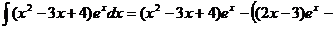
 .
.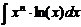
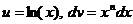 ; тогда
; тогда 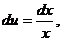
 . Следовательно,
. Следовательно, 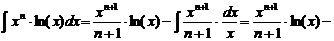

 .
.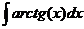
 ; тогда
; тогда 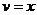 ,
,  . Следовательно,
. Следовательно, 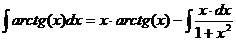 .
. . Тогда
. Тогда 
 .
.
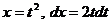 . Тогда
. Тогда  .
.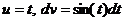 ; тогда
; тогда 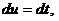
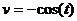 . Следовательно,
. Следовательно, 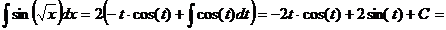
 .
.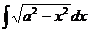
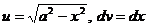 ; тогда
; тогда 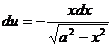 ,
, 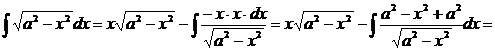
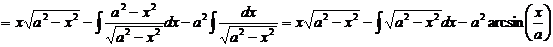 .
.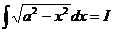 . Тогда
. Тогда  .
.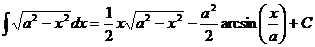 .
.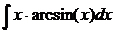
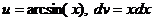 ; тогда
; тогда 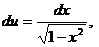
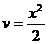 . Следовательно,
. Следовательно, 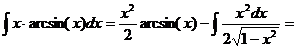

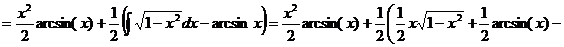
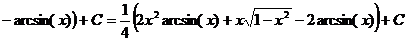 .
.
 тогда
тогда 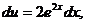
 . Следовательно,
. Следовательно, 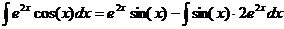 .
. тогда
тогда 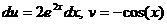 . Получается,
. Получается, =
=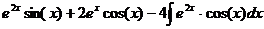 .
.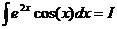 . Тогда
. Тогда 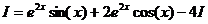 .
.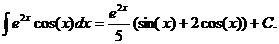
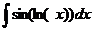
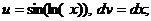 тогда
тогда 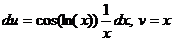 . Следовательно,
. Следовательно,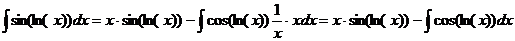 .
. тогда
тогда 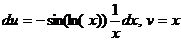 . Получается,
. Получается,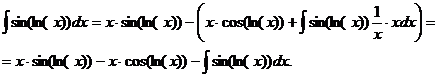
 . Тогда
. Тогда 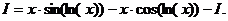
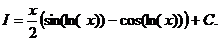


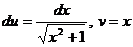 .
.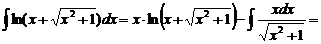


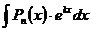 ,
,
 ,
,
 .
.
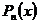 , а за dv все остальные подынтегральные выражения.
, а за dv все остальные подынтегральные выражения.
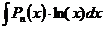 ,
,
 ,
,
 ,
,
 ,
,
 .
.
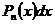 , а за u все остальные подынтегральные выражения.
, а за u все остальные подынтегральные выражения.
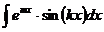 ,
,
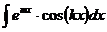 ,
,
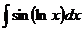 ,
,
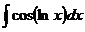 .
.
 , a > 0.
, a > 0.
 :
: – эллиптический интеграл 1 рода;
– эллиптический интеграл 1 рода;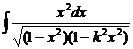 – эллиптический интеграл 2 рода;
– эллиптический интеграл 2 рода;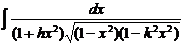 – эллиптический интеграл 3 рода.
– эллиптический интеграл 3 рода.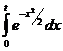 - интеграл Пуассона[2].
- интеграл Пуассона[2]. - интегралы Френеля[3].
- интегралы Френеля[3]. - интегральный логарифм.
- интегральный логарифм. - интегральная показательная функция.
- интегральная показательная функция.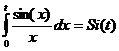 - интегральный синус.
- интегральный синус.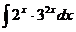 Ответ:
Ответ: 
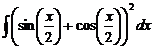 Ответ:
Ответ: 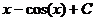
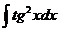 Ответ:
Ответ: 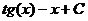
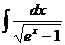 Ответ:
Ответ: 
 Ответ:
Ответ: 
 Ответ:
Ответ: 
 Ответ:
Ответ: 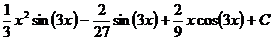
 Ответ:
Ответ: 
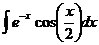 Ответ:
Ответ: 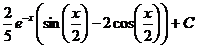
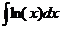 Ответ:
Ответ: 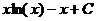
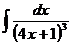 Ответ:
Ответ: 
 Ответ:
Ответ: 
 Ответ:
Ответ: 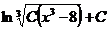
 Ответ:
Ответ: 
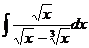 Ответ:
Ответ: 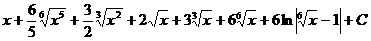
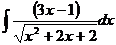 Ответ:
Ответ: 
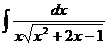 Ответ:
Ответ: 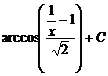
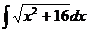 Ответ:
Ответ: 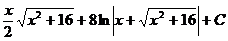
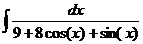 Ответ:
Ответ: 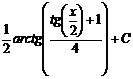
 Ответ:
Ответ: 
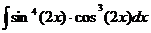 Ответ:
Ответ: 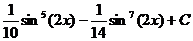
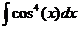 Ответ:
Ответ: 
 Ответ:
Ответ: 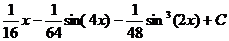
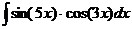 Ответ:
Ответ: 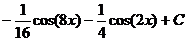
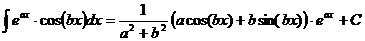 ;
; ;
; .
.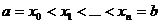 . На каждом отрезке
. На каждом отрезке  длины
длины 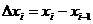 выберем произвольную точку
выберем произвольную точку 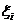 . Составим сумму
. Составим сумму 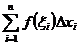 , называемую интегральной суммой для функции f (x) на отрезке [a, b].
, называемую интегральной суммой для функции f (x) на отрезке [a, b].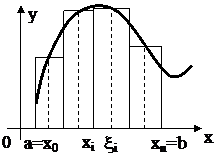 максимальной из длин отрезков разбиения:
максимальной из длин отрезков разбиения:  , этот предел конечен и не зависит от способов разбиения отрезка [a, b] на части и выбора точек
, этот предел конечен и не зависит от способов разбиения отрезка [a, b] на части и выбора точек 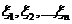 , на отрезках
, на отрезках  .
.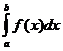 , где а называется нижним пределом, b называется верхним пределом, х называется переменной интегрирования, f (x) называется подынтегральной функцией, f (x) dx называется подынтегральным выражением, [ a, b ] – отрезок интегрирования.
, где а называется нижним пределом, b называется верхним пределом, х называется переменной интегрирования, f (x) называется подынтегральной функцией, f (x) dx называется подынтегральным выражением, [ a, b ] – отрезок интегрирования. . Фигура, ограниченная сверху графиком функции
. Фигура, ограниченная сверху графиком функции 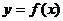 , снизу – осью Ox, сбоку прямыми x = a и x = b, называется криволинейной трапецией.
, снизу – осью Ox, сбоку прямыми x = a и x = b, называется криволинейной трапецией.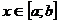 , то величина интеграла будет изменяться. Интеграл:
, то величина интеграла будет изменяться. Интеграл: 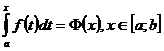 , называется определённым интегралом с переменным верхним пределом и является функцией верхнего предела х.
, называется определённым интегралом с переменным верхним пределом и является функцией верхнего предела х. имеет первообразную, равную интегралу
имеет первообразную, равную интегралу  , и тогда согласно определению неопределённого интеграла имеет место равенство
, и тогда согласно определению неопределённого интеграла имеет место равенство  .
.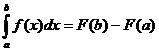 – это выражение известно под названием формулы Ньютона – Лейбница [4].
– это выражение известно под названием формулы Ньютона – Лейбница [4].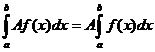 .
.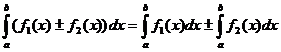 .
. .
.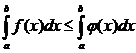 .
.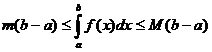 .
.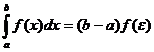 .
.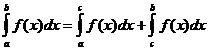 , где равенство выполняется, если существует каждый из входящих в него интегралов.
, где равенство выполняется, если существует каждый из входящих в него интегралов. .
.
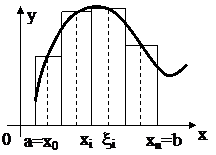 Пусть на отрезке [ a, b ] задана непрерывная функция f (x).
Пусть на отрезке [ a, b ] задана непрерывная функция f (x).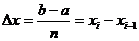 , где x1, x2, … xn – точки разбиения. Тогда можно записать, что
, где x1, x2, … xn – точки разбиения. Тогда можно записать, что 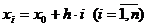 .
.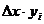 , где
, где 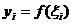 , а
, а 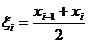 – некоторая точка на отрезке, которая в частности выбирается середина отрезка
– некоторая точка на отрезке, которая в частности выбирается середина отрезка 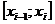 .
.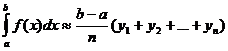 .
.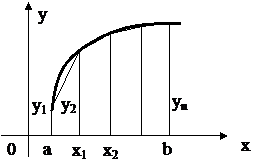 Эта формула является более точной по сравнению с формулой прямоугольников.
Эта формула является более точной по сравнению с формулой прямоугольников. ;
;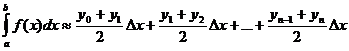 .
.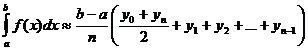
 Данный метод основан на разбиении дуги линии f (x), соответствующую [ a, b ], дугами парабол, что позволяет получить более точную формулу приближенного вычисления. Для этого разделим отрезок интегрирования [ a, b ] на четное число отрезков (2 m).
Данный метод основан на разбиении дуги линии f (x), соответствующую [ a, b ], дугами парабол, что позволяет получить более точную формулу приближенного вычисления. Для этого разделим отрезок интегрирования [ a, b ] на четное число отрезков (2 m).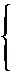
 (1)
(1)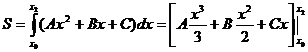 Если обозначим
Если обозначим  и примем х0 = - h, x 1 = 0, x 2 = h, то
и примем х0 = - h, x 1 = 0, x 2 = h, то 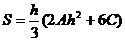 (2)
(2)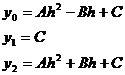
 .
.
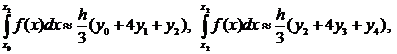 ...
...
 с помощью формулы Симпсона и формулы трапеций, разбив отрезок интегрирования на 10 частей. По формуле Симпсона получим:
с помощью формулы Симпсона и формулы трапеций, разбив отрезок интегрирования на 10 частей. По формуле Симпсона получим:
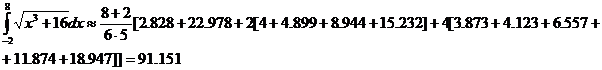
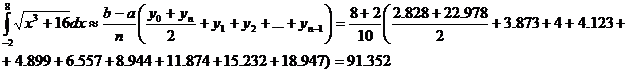
 определена и непрерывна на любом отрезке [ a, b ], то несобственным интегралом с бесконечным пределом или несобственным интегралом первого рода называется интеграл:
определена и непрерывна на любом отрезке [ a, b ], то несобственным интегралом с бесконечным пределом или несобственным интегралом первого рода называется интеграл: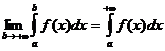 или
или  , или
, или , с – произвольное число.
, с – произвольное число.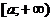 непрерывные функции
непрерывные функции 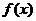 и
и 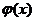 удовлетворяют условию:
удовлетворяют условию:  , то из сходимости интеграла
, то из сходимости интеграла  следует сходимости интеграла
следует сходимости интеграла 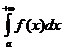 , а из расходимости интеграла
, а из расходимости интеграла 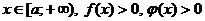 и существует конечные предел
и существует конечные предел 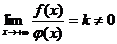 , то интегралы
, то интегралы 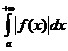 , то сходится и интеграл
, то сходится и интеграл  - не существует
- не существует 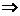 несобственный интеграл расходится.
несобственный интеграл расходится.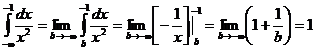 - интеграл сходится.
- интеграл сходится. и имеет разрыв II-го рода при
и имеет разрыв II-го рода при  , то несобственным интегралом неограниченной функции или несобственным интегралом второго родва называется интеграл:
, то несобственным интегралом неограниченной функции или несобственным интегралом второго родва называется интеграл:  или
или  , если функция терпит бесконечный разрыв в точке
, если функция терпит бесконечный разрыв в точке  .
.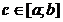 , то несобственным интегралом второго рода называют интеграл:
, то несобственным интегралом второго рода называют интеграл: 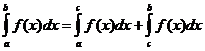 .
.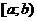 функции
функции 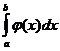 следует сходимости интеграла
следует сходимости интеграла 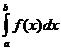 , а из расходимости интеграла
, а из расходимости интеграла 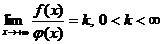 , то интегралы
, то интегралы 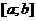 , имеет разрыв в точке
, имеет разрыв в точке  сходится, то сходится и интеграл
сходится, то сходится и интеграл 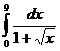 Ответ: 6-2ln4
Ответ: 6-2ln4 Ответ:
Ответ: 
 Ответ: 0
Ответ: 0 Ответ:
Ответ: 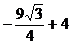
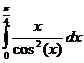 Ответ:
Ответ: 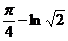
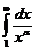 Ответ:
Ответ: 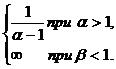
 Ответ: π
Ответ: π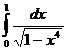 Ответ: сходится
Ответ: сходится Ответ: расходится
Ответ: расходится Ответ: сходится
Ответ: сходится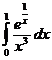 Ответ: расходится
Ответ: расходится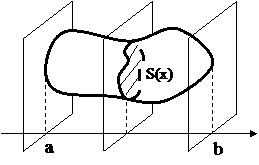 Пусть тело, заключеное между двумя плоскостями x = a и x = b, имеет площадь сечения S (x) при
Пусть тело, заключеное между двумя плоскостями x = a и x = b, имеет площадь сечения S (x) при  , проведенного перпендикулярно к оси Ох, и которое является известной и непрерывной изменяющейся при изменении х.
, проведенного перпендикулярно к оси Ох, и которое является известной и непрерывной изменяющейся при изменении х. .
.



