
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод непосредственного интегрированияСодержание книги
Поиск на нашем сайте Метод интегрирования основан на применении табличных интегралов, и называется непосредственным интегрированием. При этом данный интеграл может быть приведен к табличному с помощью тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла. Примеры: a) b)
с) Замена переменной Этот метод интегрирования основан на введении новой переменной интегрирования. Приведем пример: пусть дана сложная функция f (x), где Эта формула называется формулой замены переменной в неопределенном интеграле. Примеры: a)
b)
с) Первый вариант замены: Второй вариант замены:
d)
Второй вариант замены: = При интегрировании заменой переменной важно удачно сделать подстановку. Однако нельзя дать общее правило выбора замены переменной для интегрирования любой функции. Это можно сделать только для интегрирования отдельных классов функций: рациональных, тригонометрических и т.д. (интегрирование этих классов функций предложены в таблицах 3 – 7). Интегрирование по частям Этот метод интегрирования основан на применении формулы дифференцирования произведения d (uv)= udv + vdu и вычислении затем интеграла Примеры: a) Интегирируется по частям: пусть Еще раз интегрируется по частям: пусть
b) Интегирируется по частям: пусть
c) Интегирируется по частям: пусть Получившийся интеграл вычисляется методом замены переменной:
d) Пусть Интегирируется по частям: пусть
e) Интегирируется по частям: пусть
Обозначается, Следовательно, f) Интегирируется по частям: пусть
g) Интегрируется по частям: пусть Еще раз интегрируется по частям: пусть
= Обозначается, Следовательно, h) Интегрируется по частям: пусть
Еще раз интегрируется по частям: пусть
Обозначают, Следовательно, k) Интегрируется по частям: пусть тогда Следовательно,
Приведем в таблице 2 некоторые распространённые случаи использования метода интегрирования по частям. Таблица 2.
|
||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 177; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |


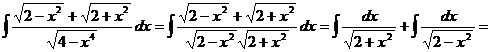
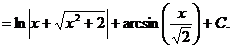
 .
. - функция имеющая непрерывную производную
- функция имеющая непрерывную производную  . Применяется свойство инвариантности формулы интегрирования неопределенного интеграла, получаем:
. Применяется свойство инвариантности формулы интегрирования неопределенного интеграла, получаем:  .
.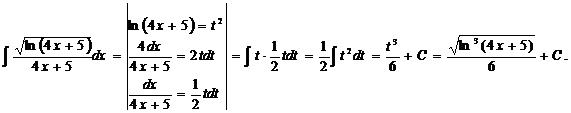
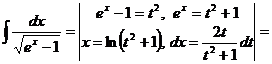

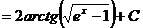 .
.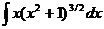 .
.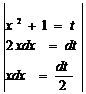 =
= 
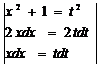 =
= 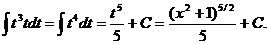
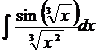 . Первый вариант замены:
. Первый вариант замены: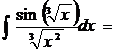
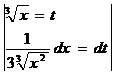 =
= 
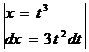 =
= 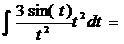
 . Из этого равества получаем формулу интегрирования по частям:
. Из этого равества получаем формулу интегрирования по частям:  .
.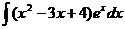
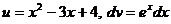 ; тогда
; тогда 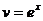 ,
, 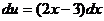 . Следовательно,
. Следовательно, 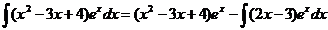 .
.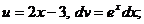 тогда
тогда 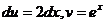 . Получаем,
. Получаем, 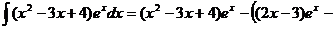
 .
.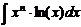
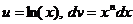 ; тогда
; тогда 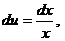
 . Следовательно,
. Следовательно, 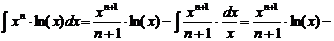

 .
.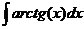
 ; тогда
; тогда  ,
,  . Следовательно,
. Следовательно, 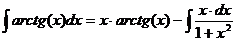 .
. . Тогда
. Тогда 
 .
.
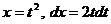 . Тогда
. Тогда  .
.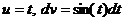 ; тогда
; тогда 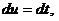
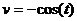 . Следовательно,
. Следовательно, 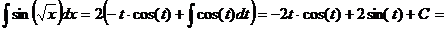
 .
.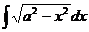
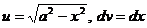 ; тогда
; тогда 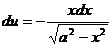 ,
, 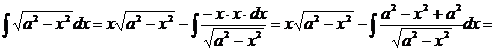
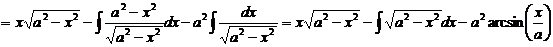 .
.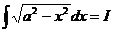 . Тогда
. Тогда  .
.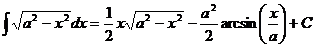 .
.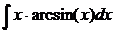
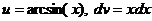 ; тогда
; тогда 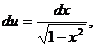
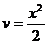 . Следовательно,
. Следовательно, 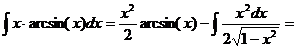

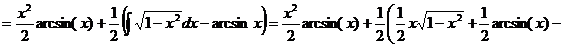
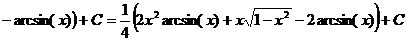 .
.
 тогда
тогда 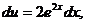
 . Следовательно,
. Следовательно, 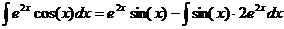 .
. тогда
тогда 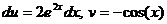 . Получается,
. Получается, =
=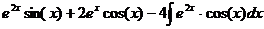 .
.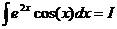 . Тогда
. Тогда 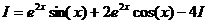 .
.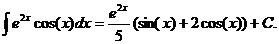
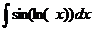
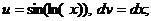 тогда
тогда 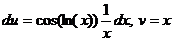 . Следовательно,
. Следовательно,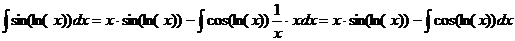 .
. тогда
тогда 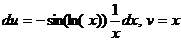 . Получается,
. Получается,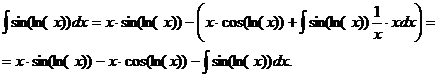
 . Тогда
. Тогда 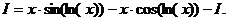
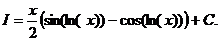


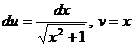 .
.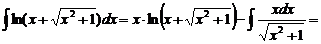


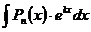 ,
,
 ,
,
 .
.
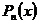 , а за dv все остальные подынтегральные выражения.
, а за dv все остальные подынтегральные выражения.
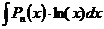 ,
,
 ,
,
 ,
,
 ,
,
 .
.
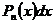 , а за u все остальные подынтегральные выражения.
, а за u все остальные подынтегральные выражения.
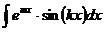 ,
,
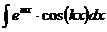 ,
,
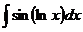 ,
,
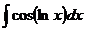 .
.
 , a > 0.
, a > 0.



